【笔试常见编程题03】统计回文、连续最大和、不要二、把字符串转换成整数

news2024/10/7 8:27:08

在这里插入图片描述

1. 统计回文

“回文串”是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串。花花非常喜欢这种拥有对称美的回文串，生日的时候她得到两个礼物分别是字符串A和字符串B。现在她非常好奇有没有办法将字符串B插入字符串A使产生的字符串是一个回文串。你接受花花的请求，帮助她寻找有多少种插入办法可以使新串是一个回文串。如果字符串B插入的位置不同就考虑为不一样的办法。

例如：
A = “aba”，B = “b”。这里有4种把B插入A的办法：

在A的第一个字母之前: “baba” 不是回文
在第一个字母‘a’之后: “abba” 是回文
在字母‘b’之后: “abba” 是回文
在第二个字母’a’之后 “abab” 不是回文

所以满足条件的答案为2
输入描述
每组输入数据共两行。第一行为字符串A 第二行为字符串B 字符串长度均小于100且只包含小写字母
输出描述
输出一个数字，表示把字符串B插入字符串A之后构成一个回文串的方法数
示例 1
输入
aba
b
输出
2

思路1：暴力求解
在每个字符的前面插入另一个字符串
判断是否是回文
判断方法：前后双指针，指向头和尾
如果一样，一个++，一个- -

bool JudgePal(string s1) // 判断是否为回文
{
    int front = 0;
    int tail = s1.size() - 1;
    while (front < tail)
    {
        if (s1[front] == s1[tail])
        {
            front++;
            tail--;
        }
        else return false;
    }
    return true;
}

int main() {
    string s1, s2;
    getline(cin, s1);
    getline(cin, s2);
    int count = 0;
    for (int i = 0; i <= s1.size(); i++)
    {
        string temp = s1;
        temp.insert(i, s2);
        if (JudgePal(temp))
            count++;
    }
    cout << count;

    return 0;
}

2. 连续最大和

一个数组有 N 个元素，求连续子数组的最大和。例如：[-1,2,1]，和最大的连续子数组为[2,1]，其和为 3
输入描述
输入为两行。第一行一个整数n(1 <= n <= 100000)，表示一共有n个元素第二行为n个数，即每个元素,每个整数都在32位int范围内。以空格分隔。
输出描述
所有连续子数组中和最大的值。
示例 1
输入
3
-1 2 1
输出
3

思路1：暴力求解

双循环求所有子数组的和
如果比int max大，更新max

时间复杂度 $O(N^2)$
在刷题软件上，如果数组元素过长
则会超出时间限制

int main() {
    size_t n;
    cin >> n;
    vector<int> v;
    v.resize(n);
    for (int i = 0; i < v.size(); i++) {
        cin >> v[i];
    }
    int max = v[0];
    for (int i = 1; i < v.size(); i++) {
        int temp = 0;
        for (int j = i; j < v.size(); j++)
        {
            temp += v[j];
            if (temp > max)
                max = temp;
        }
    }
    cout << max;
    return 0;
}

思路2：dp

dp[i]是以数组下标为 i 的数作为结尾的最大子序列和，注意是以 i 为结尾
比如说现在有一个数组 {6,-3,-2,7,-15,1,2,2}
dp[2]就是以-2为结尾的，那么显然dp[2]的最大值就是1（6，-3，-2）
dp[3]要以7结尾，那么以7结尾的子序列最大和就是8（6，-3，-2，7）
求dp[i]有两种可能
第一种就是像上面的dp[3]一样，dp[2]求出来是1了，dp[2]加上array[3]比dp[2]大
把dp[2]加上array[3]赋给dp
第二种可能就是说如果dp[2]求出来是-100，dp[2]+array[3]是-93
这时候dp[2]反而拖垮了array[3]，array[3]就是最大子序列，把array[3]赋给dp

时间复杂度 $O (N)$
空间复杂度 $O (1)$

int main()
{
    size_t n;
    cin >> n;
    vector<int> v;
    v.resize(n);
    for (int i = 0; i < v.size(); i++) {
        cin >> v[i];
    }
    int dp = v[0];
    int maxsum = v[0];
    for (int i = 1; i < v.size(); i++)
    {
        dp = max(dp + v[i], v[i]);
        maxsum = max(dp, maxsum);
    }
    cout << maxsum;
    return 0;
}

3. 不要二

二货小易有一个W*H的网格盒子，网格的行编号为0_{H-1，网格的列编号为0}W-1。每个格子至多可以放一块蛋糕，任意两块蛋糕的欧几里得距离不能等于2。
对于两个格子坐标(x1,y1),(x2,y2)的欧几里得距离为:
( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) 的算术平方根
小易想知道最多可以放多少块蛋糕在网格盒子里。
输入描述
每组数组包含网格长宽W,H，用空格分割.(1 ≤ W、H ≤ 1000)
输出描述
输出一个最多可以放的蛋糕数
示例 1
输入
3 2
输出
4

思路1：
欧几里和距离就是最短直线距离
如果是求斜线距离涉及到勾股定理
比如：坐标(x2, y2)和(x1, y1)的距离
就是一条斜线距离
x1到x2的距离为1，y1到y2的距离也为1
1的平方加1的平方的算术平方根就是斜线距离
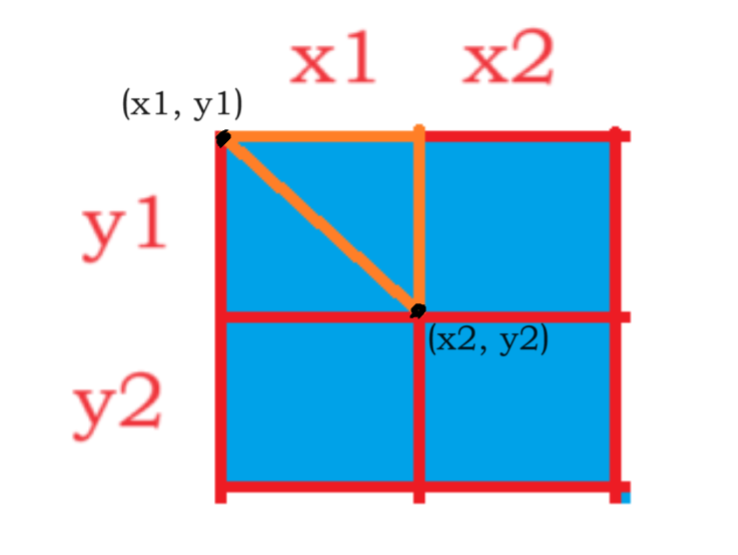
在这里插入图片描述
斜线距离是一定不为2的
所以只需要考虑横纵为2的距离不能放蛋糕
如图所示
横排第一和二个格子放蛋糕
第三和四就不能放蛋糕
竖排也是一样

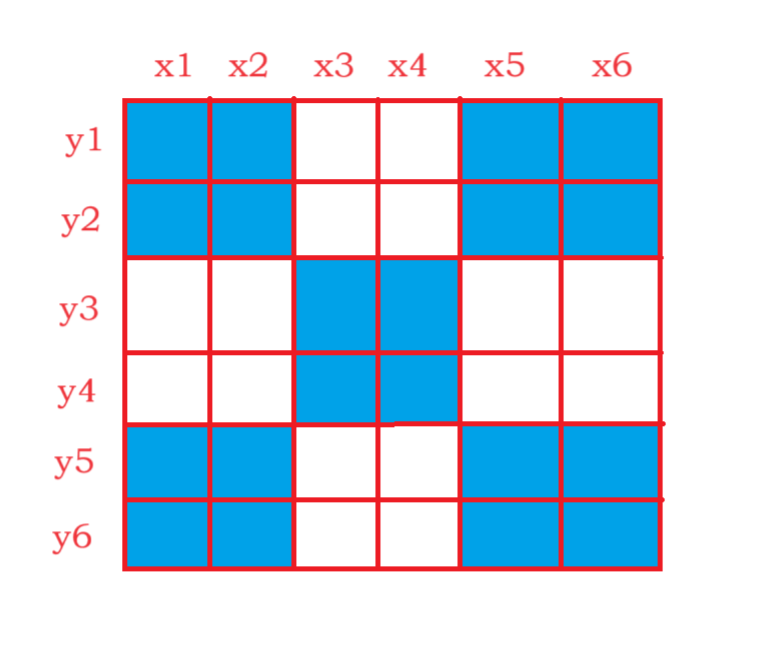
第一排前两个格子是一定能放蛋糕的
第二排也是，放蛋糕是占先手的
也就是说放蛋糕的数量一定大于等于总格子的一半
如果横纵乘积模4为0，放蛋糕的数量就是横纵乘积除2
如果横纵乘积模4不为0，则需要看横和纵分别能不能整除2
如果能：放蛋糕数量 = 横纵乘积 + 2
如果不能：放蛋糕数量 = 横纵乘积 + 1

int main() {
    int W, H;
    cin >> W >> H;
    cout << W*H/2 + (!(W*H%4) ? 0 : (W % 2 == 0 && H % 2 == 0 ? 2 : 1));

    return 0;
}

4. 把字符串转换成整数

将一个字符串转换成一个整数，要求不能使用字符串转换整数的库函数。数值为 0 或者字符串不是一个合法的数值则返回 0
数据范围：字符串长度满足
进阶：空间复杂度，时间复杂度
注意：
①字符串中可能出现任意符号，出现除 +/- 以外符号时直接输出 0
②字符串中可能出现 +/- 且仅可能出现在字符串首位。
示例 1
输入
“+2147483647”
输出
2147483647
示例 2
输入
“1a33”
输出
0

思路1：

首先判断第一个字符
然后遍历字符串转换成数字加到num

转换出的整数可能超出整型能存储的最大值
需要判断一下
代码1从字符串最后往前取字符
加到num里面，代码有些难理解

class Solution {
public:
    int StrToInt(string str) {
        long long num = 0; 
        int i = str.size() - 1;
        if ((str[0] < '0' || str[0] > '9') && (str[0] != '-' && str[0] != '+'))
            return 0;
        int power = 0;
        while (i >= 0)
        {
            if (str[i] >= '0' && str[i] <= '9')
                num += (str[i--] - '0') * pow(10, power++);
            else if (i == 0 && (str[i] == '-' || str[i] == '+'))
                break;
            else if (num > 0x7fffffff || str[i] < '0' || str[i] > '9') // 字符串转换出的整型可能超出了整形能存储的最大值,所以需要判断一下
                return 0;
        }
        if (str[0] == '-')
            return -num;
         return num;  
    }
};

代码2从字符串第一个字符往后取字符
加到num里面

class Solution {
public:
    int StrToInt(string str) {
        long long num = 0; 
        int i = 0;
        if (str[0] == '-' || str[0] == '+')
            i++;
        while (i < str.size()){
            if (str[i] >= '0' && str[i] <= '9')
                num = num * 10 + (str[i++] - '0');
            else if (num > 0x7fffffff || str[i] < '0' || str[i] > '9') // 字符串转换出的整型可能超出了整形能存储的最大值,所以需要判断一下
                return 0;
        }
        if (str[0] == '-')
            return -num;
         return num;  
    }
};