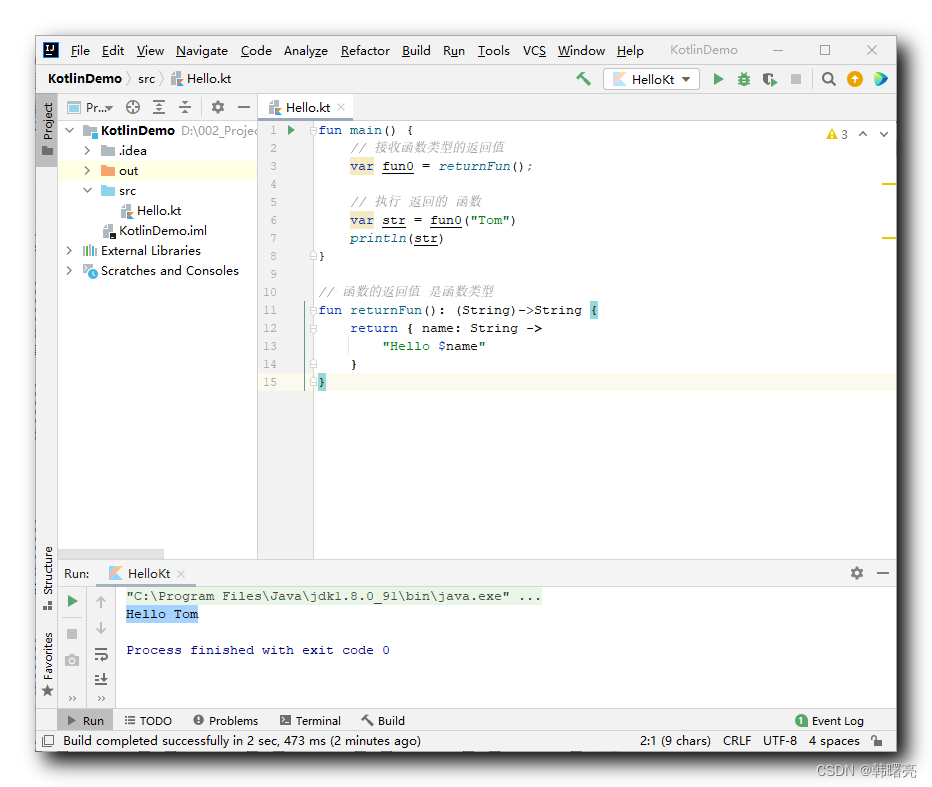
小蓝本 第一本 《因式分解技巧》 第八章 多项式的一次因式 笔记 (第八天)
- 前言
- 余数定理
- 有理根求法
- 第一步
- 第二步(可能有理根多的情况下,可以用)
- 第三步
- 快速识别特殊有理根
- 情况1
- 情况2
- 求解
- 注意
- 习题8
- 题目
- 题解
- 改错
前言
坚持的第8天,因为期末考试,小蓝本放海了n周,从今天开始继续
余数定理
用 f ( x ) 表示多项式 用f(x)表示多项式 用f(x)表示多项式 anxn + an-1xn-1 + …… + a1x + a0
若用一个一次多项式 x − c x-c x−c 作除式去除多项式 f ( x ) f(x) f(x),余式是一个数 r r r,商式为多项式 Q ( x ) Q(x) Q(x)
f ( x ) = ( x − c ) Q ( x ) + r f(x)=(x-c)Q(x)+r f(x)=(x−c)Q(x)+r
※ 重点来了,若使 x = c x=c x=c 会得 f ( c ) = r f(c)=r f(c)=r, ∴ x − c 除 f ( x ) 时,所得的余数为 f ( c ) x-c除f(x)时,所得的余数为f(c) x−c除f(x)时,所得的余数为f(c), f ( c ) = 0 f(c)=0 f(c)=0对因式分解结果是一个既约多项式有很大帮助。
当
f
(
c
)
=
0
f(c)=0
f(c)=0时, 称
c
为多项式
f
(
x
)
的根
c为多项式f(x)的根
c为多项式f(x)的根
综上可得到结论
∵
f
(
c
)
=
0
f(c)=0
f(c)=0
∴
x
−
c
是
f
(
x
)
的因式
x-c是f(x)的因式
x−c是f(x)的因式
或
∵
x
−
c
是
f
(
x
)
的因式
x-c是f(x)的因式
x−c是f(x)的因式
∴
f
(
c
)
=
0
f(c)=0
f(c)=0
有理根求法
说了这么多概念,还没提到有理根的求法。
若使 f ( c ) = 0 f(c)=0 f(c)=0且不知道任何有关结论,这无疑是大海捞针,下面提供3步确定有理根求法
第一步
假定 f ( x ) f(x) f(x)是整系数多项式(及所有项的系数均为整数), c = p / q ( p , q 为互质的整数) c=p/q(p,q为互质的整数) c=p/q(p,q为互质的整数)
∵
f
(
c
)
=
0
f(c)=0
f(c)=0
∴ an(p/q)n + an-1(p/q)n-1 + …… + a1(p/q) + a0 = 0
等式 2边同乘
q
n
q^n
qn
∴anpn + an-1pn-1q + …… + a1pqn-1 + a0qn = 0
∵等式右边分别被p和q整除
∴an被q整除,a0被p整除
综上 有理根 c = p / q c=p/q c=p/q的分子p是常数项a0的因数,分母q是首项系数an的因数
第二步(可能有理根多的情况下,可以用)
Q(x)是整系数多项式的证明过程(
f
(
x
)
也是整系数多项式
f(x)也是整系数多项式
f(x)也是整系数多项式)


判别法: f ( x ) f(x) f(x)是整系数多项式,经过第一步的处理,如果 q − p q-p q−p不是 f ( 1 ) f(1) f(1)的因数时,那么 p / q p/q p/q不是 f ( x ) f(x) f(x)的根
证明:
假设p/q是
f
(
x
)
f(x)
f(x)的根
f
(
x
)
=
(
q
x
−
p
)
Q
(
x
)
f(x)=(qx-p)Q(x)
f(x)=(qx−p)Q(x)
若x=1
f
(
1
)
=
(
q
−
p
)
Q
(
1
)
f(1)=(q-p)Q(1)
f(1)=(q−p)Q(1)
∵Q(x)是整系数多项式
∴Q(1)是整数(才有因数)
∴
q
−
p
q-p
q−p不是
f
(
1
)
f(1)
f(1)的因数时,
p
/
q
p/q
p/q不是
f
(
x
)
的根
f(x)的根
f(x)的根
第三步
若经过前2步仍旧有很多根的可能,直接一一代入
快速识别特殊有理根
情况1
∵
f
(
x
)
f(x)
f(x)的所有系数之和为0
∴
f
(
x
)
f(x)
f(x)的根为1
情况2
∵
f
(
x
)
f(x)
f(x)所有奇次项系数之和 = 所有偶次项系数之和
∴
f
(
x
)
f(x)
f(x)的根为-1
求解
主要运用到拆项和提公因式内容
https://cnbjhacker.blog.csdn.net/article/details/128226734 提公因式
https://cnbjhacker.blog.csdn.net/article/details/128272204 拆项
注意
当 c = p / q ( q > 1 ) c=p/q(q>1) c=p/q(q>1)(根为分数) x − p / q 推成 q x − p x-p/q 推成 qx-p x−p/q推成qx−p
习题8
题目

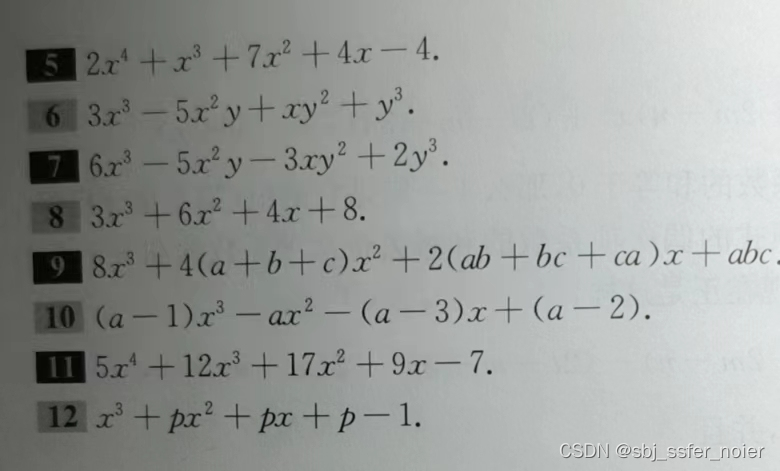
题解
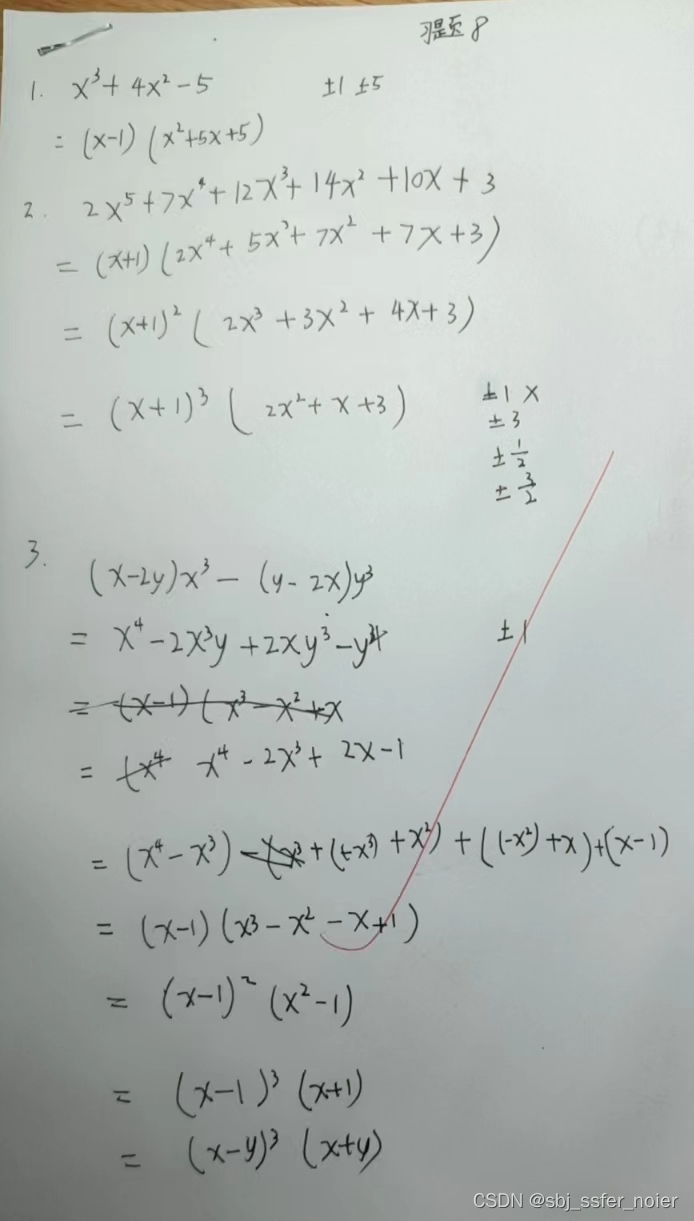
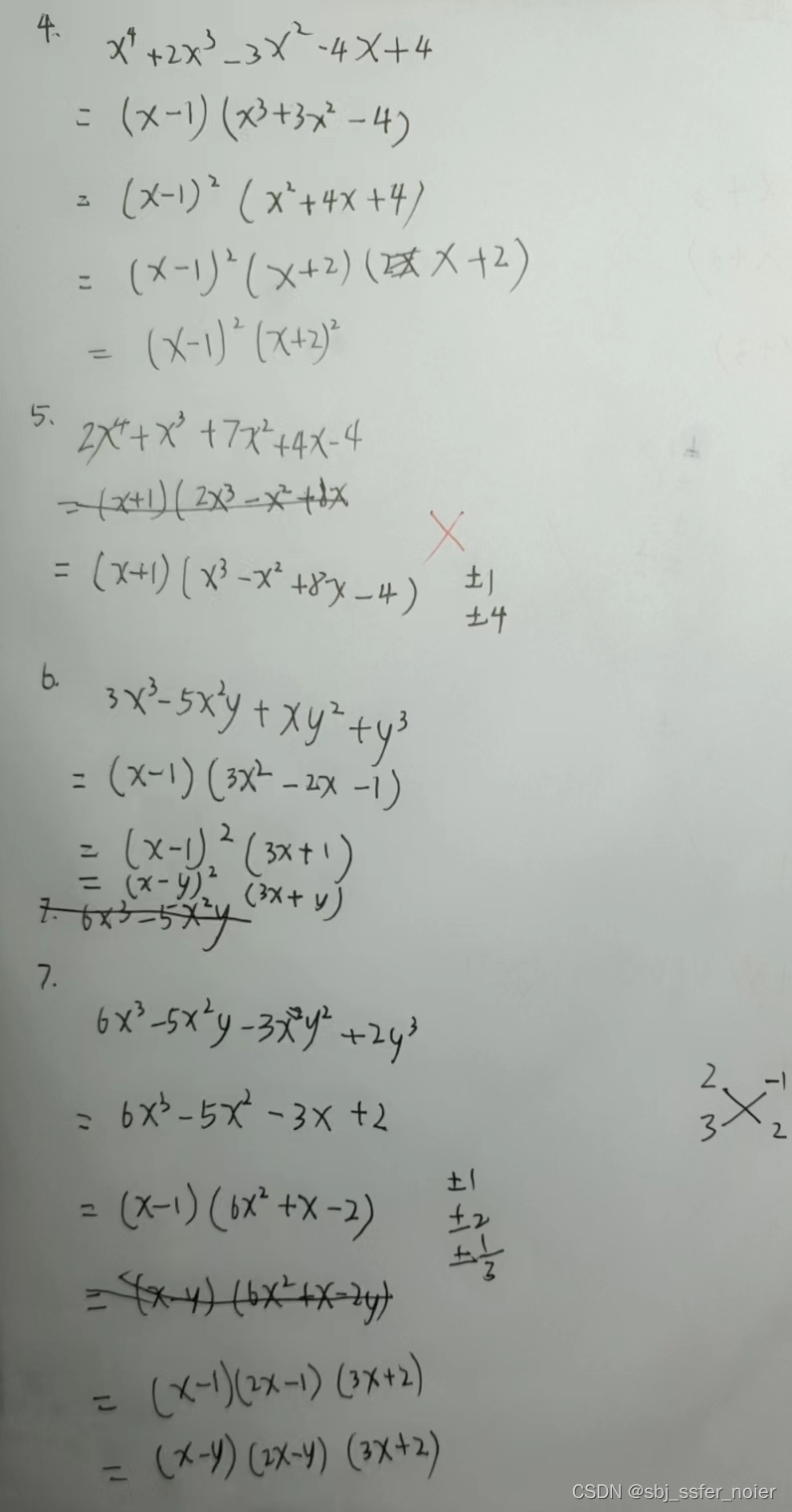

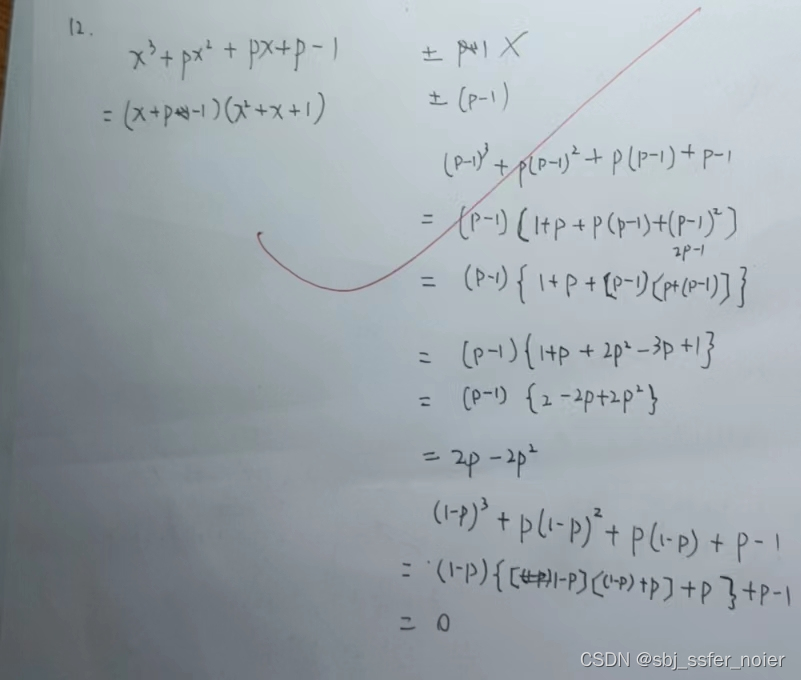
改错
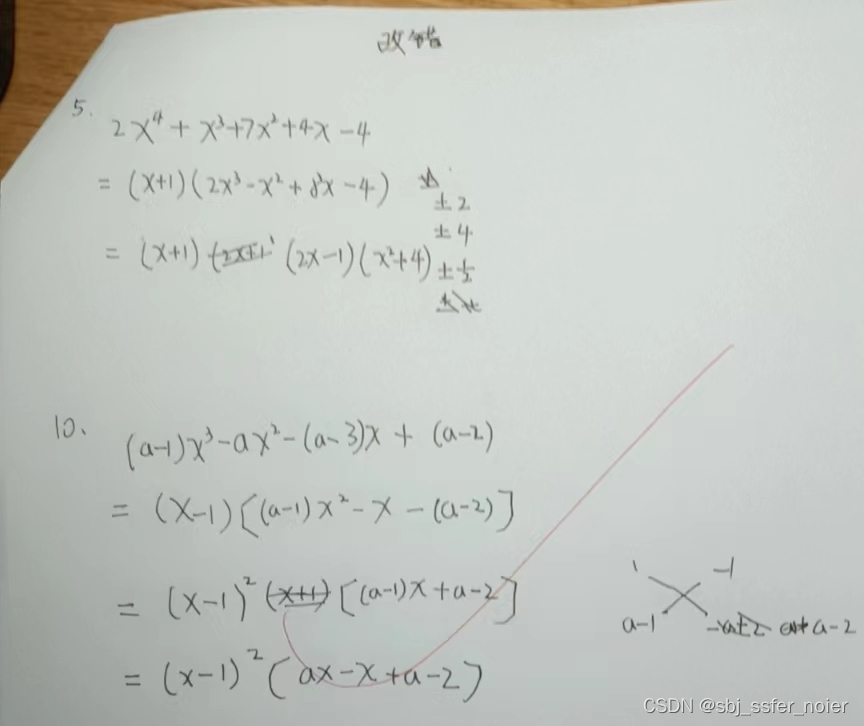



![JdbcUtils工具类的优化升级——通过配置文件连接mysql8.0,并对mysql8.0中的表进行[简单查询]操作](https://img-blog.csdnimg.cn/9bae8ccb7269403e9911afec07182d46.png)