二叉树18：从中序与后序遍历序列构造二叉树

主要是我自己刷题的一些记录过程。如果有错可以指出哦，大家一起进步。
转载代码随想录
原文链接：
代码随想录
leetcode链接：344. 反转字符串

题目：

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗二叉树。

示例：

示例 1:
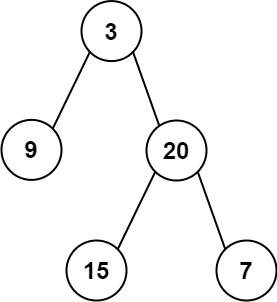
在这里插入图片描述

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示：

1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由 不同 的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历

思路：

其实这个题我看到是一点思路都没有。推荐你们看看卡哥的视频吧。我这边只是做个记录。

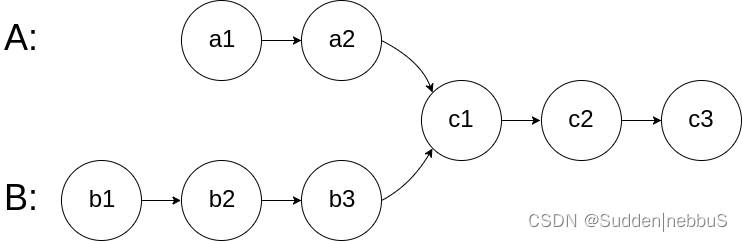
首先回忆一下如何根据两个顺序构造一个唯一的二叉树，相信理论知识大家应该都清楚，就是以后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。

如果让我们肉眼看两个序列，画一棵二叉树的话，应该分分钟都可以画出来。

流程如图：
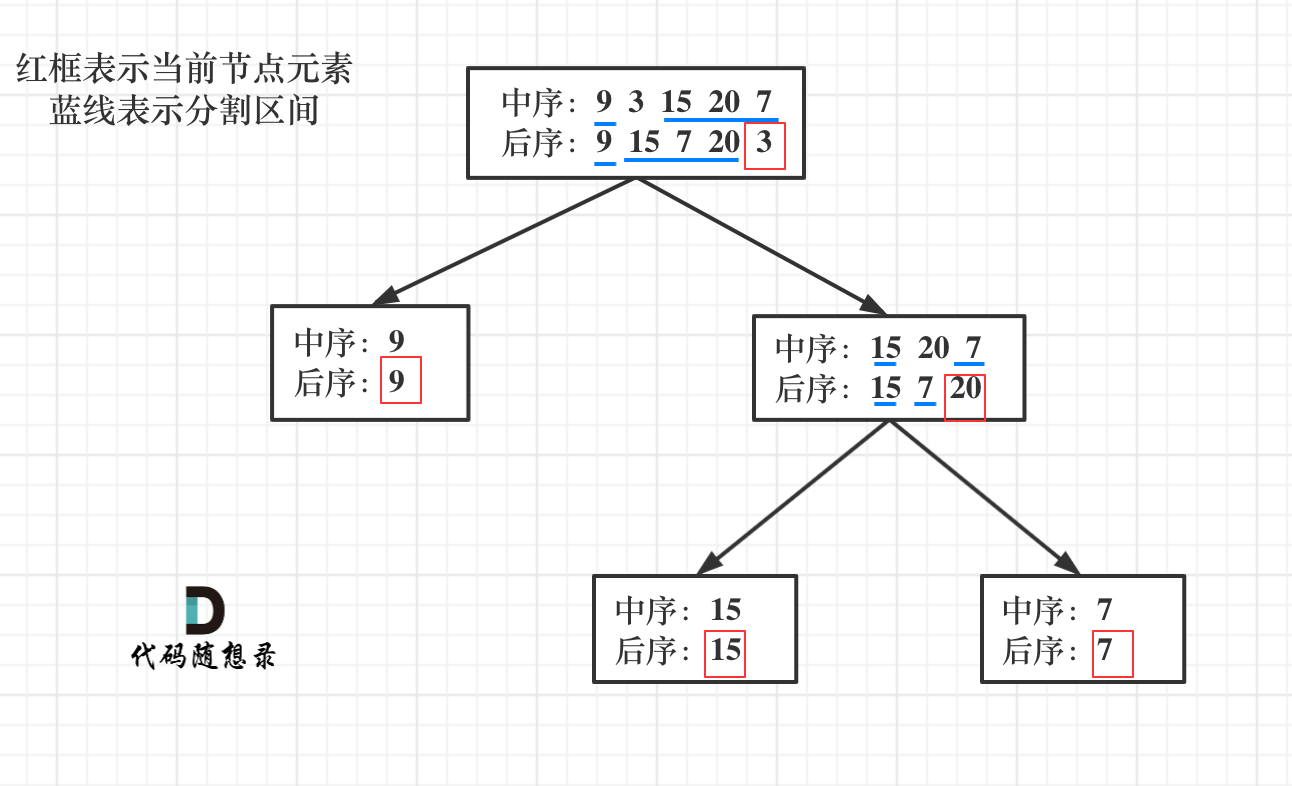在这里插入图片描述那么代码应该怎么写呢？

说到一层一层切割，就应该想到了递归。

来看一下一共分几步：

第一步：如果数组大小为零的话，说明是空节点了。
第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）
第五步：切割后序数组，切成后序左数组和后序右数组
第六步：递归处理左区间和右区间

不难写出如下代码：（先把框架写出来）

TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {

    // 第一步
    if (postorder.size() == 0) return NULL;

    // 第二步：后序遍历数组最后一个元素，就是当前的中间节点
    int rootValue = postorder[postorder.size() - 1];
    TreeNode* root = new TreeNode(rootValue);

    // 叶子节点
    if (postorder.size() == 1) return root;

    // 第三步：找切割点
    int delimiterIndex;
    for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
        if (inorder[delimiterIndex] == rootValue) break;
    }

    // 第四步：切割中序数组，得到 中序左数组和中序右数组
    // 第五步：切割后序数组，得到 后序左数组和后序右数组

    // 第六步
    root->left = traversal(中序左数组, 后序左数组);
    root->right = traversal(中序右数组, 后序右数组);

    return root;
}

难点大家应该发现了，就是如何切割，以及边界值找不好很容易乱套。

此时应该注意确定切割的标准，是左闭右开，还有左开右闭，还是左闭右闭，这个就是不变量，要在递归中保持这个不变量。

在切割的过程中会产生四个区间，把握不好不变量的话，一会左闭右开，一会左闭右闭，必然乱套！

可见循环不变量的重要性，在二分查找以及螺旋矩阵的求解中，坚持循环不变量非常重要，本题也是。

首先要切割中序数组，为什么先切割中序数组呢？

切割点在后序数组的最后一个元素，就是用这个元素来切割中序数组的，所以必要先切割中序数组。

中序数组相对比较好切，找到切割点（后序数组的最后一个元素）在中序数组的位置，然后切割，如下代码中我坚持左闭右开的原则：

// 找到中序遍历的切割点
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
    if (inorder[delimiterIndex] == rootValue) break;
}

// 左闭右开区间：[0, delimiterIndex)
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
// [delimiterIndex + 1, end)
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );

接下来就要切割后序数组了。

首先后序数组的最后一个元素指定不能要了，这是切割点也是当前二叉树中间节点的元素，已经用了。

后序数组的切割点怎么找？

后序数组没有明确的切割元素来进行左右切割，不像中序数组有明确的切割点，切割点左右分开就可以了。

此时有一个很重的点，就是中序数组大小一定是和后序数组的大小相同的（这是必然）。

中序数组我们都切成了左中序数组和右中序数组了，那么后序数组就可以按照左中序数组的大小来切割，切成左后序数组和右后序数组。

代码如下：

// postorder 舍弃末尾元素，因为这个元素就是中间节点，已经用过了
postorder.resize(postorder.size() - 1);

// 左闭右开，注意这里使用了左中序数组大小作为切割点：[0, leftInorder.size)
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
// [leftInorder.size(), end)
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());

此时，中序数组切成了左中序数组和右中序数组，后序数组切割成左后序数组和右后序数组。

接下来可以递归了，代码如下：

root->left = traversal(leftInorder, leftPostorder);
root->right = traversal(rightInorder, rightPostorder);

完整代码如下：
C++完整代码

class Solution {
private:
    TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
        if (postorder.size() == 0) return NULL;

        // 后序遍历数组最后一个元素，就是当前的中间节点
        int rootValue = postorder[postorder.size() - 1];
        TreeNode* root = new TreeNode(rootValue);

        // 叶子节点
        if (postorder.size() == 1) return root;

        // 找到中序遍历的切割点
        int delimiterIndex;
        for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }

        // 切割中序数组
        // 左闭右开区间：[0, delimiterIndex)
        vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
        // [delimiterIndex + 1, end)
        vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );

        // postorder 舍弃末尾元素
        postorder.resize(postorder.size() - 1);

        // 切割后序数组
        // 依然左闭右开，注意这里使用了左中序数组大小作为切割点
        // [0, leftInorder.size)
        vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
        // [leftInorder.size(), end)
        vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());

        root->left = traversal(leftInorder, leftPostorder);
        root->right = traversal(rightInorder, rightPostorder);

        return root;
    }
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if (inorder.size() == 0 || postorder.size() == 0) return NULL;
        return traversal(inorder, postorder);
    }
};

相信大家自己就算是思路清晰，代码写出来一定是各种问题，所以一定要加日志来调试，看看是不是按照自己思路来切割的，不要大脑模拟，那样越想越糊涂。
加了日志的代码如下：（加了日志的代码不要在leetcode上提交，容易超时）

class Solution {
private:
    TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
        if (postorder.size() == 0) return NULL;

        int rootValue = postorder[postorder.size() - 1];
        TreeNode* root = new TreeNode(rootValue);

        if (postorder.size() == 1) return root;

        int delimiterIndex;
        for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }

        vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
        vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );

        postorder.resize(postorder.size() - 1);

        vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
        vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());

        // 以下为日志
        cout << "----------" << endl;

        cout << "leftInorder :";
        for (int i : leftInorder) {
            cout << i << " ";
        }
        cout << endl;

        cout << "rightInorder :";
        for (int i : rightInorder) {
            cout << i << " ";
        }
        cout << endl;

        cout << "leftPostorder :";
        for (int i : leftPostorder) {
            cout << i << " ";
        }
        cout << endl;
         cout << "rightPostorder :";
        for (int i : rightPostorder) {
            cout << i << " ";
        }
        cout << endl;

        root->left = traversal(leftInorder, leftPostorder);
        root->right = traversal(rightInorder, rightPostorder);

        return root;
    }
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if (inorder.size() == 0 || postorder.size() == 0) return NULL;
        return traversal(inorder, postorder);
    }
};

此时应该发现了，如上的代码性能并不好，因为每层递归定义了新的vector（就是数组），既耗时又耗空间，但上面的代码是最好理解的，为了方便读者理解，所以用如上的代码来讲解。

下面给出用下标索引写出的代码版本：（思路是一样的，只不过不用重复定义vector了，每次用下标索引来分割）
C++优化版本

class Solution {
private:
    // 中序区间：[inorderBegin, inorderEnd)，后序区间[postorderBegin, postorderEnd)
    TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
        if (postorderBegin == postorderEnd) return NULL;

        int rootValue = postorder[postorderEnd - 1];
        TreeNode* root = new TreeNode(rootValue);

        if (postorderEnd - postorderBegin == 1) return root;

        int delimiterIndex;
        for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }
        // 切割中序数组
        // 左中序区间，左闭右开[leftInorderBegin, leftInorderEnd)
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = delimiterIndex;
        // 右中序区间，左闭右开[rightInorderBegin, rightInorderEnd)
        int rightInorderBegin = delimiterIndex + 1;
        int rightInorderEnd = inorderEnd;

        // 切割后序数组
        // 左后序区间，左闭右开[leftPostorderBegin, leftPostorderEnd)
        int leftPostorderBegin =  postorderBegin;
        int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
        // 右后序区间，左闭右开[rightPostorderBegin, rightPostorderEnd)
        int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
        int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素，已经作为节点了

        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  postorder, leftPostorderBegin, leftPostorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);

        return root;
    }
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if (inorder.size() == 0 || postorder.size() == 0) return NULL;
        // 左闭右开的原则
        return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
    }
};

那么这个版本写出来依然要打日志进行调试，打日志的版本如下：（该版本不要在leetcode上提交，容易超时）

class Solution {
private:
    TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
        if (postorderBegin == postorderEnd) return NULL;

        int rootValue = postorder[postorderEnd - 1];
        TreeNode* root = new TreeNode(rootValue);

        if (postorderEnd - postorderBegin == 1) return root;

        int delimiterIndex;
        for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }
        // 切割中序数组
        // 左中序区间，左闭右开[leftInorderBegin, leftInorderEnd)
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = delimiterIndex;
        // 右中序区间，左闭右开[rightInorderBegin, rightInorderEnd)
        int rightInorderBegin = delimiterIndex + 1;
        int rightInorderEnd = inorderEnd;

        // 切割后序数组
        // 左后序区间，左闭右开[leftPostorderBegin, leftPostorderEnd)
        int leftPostorderBegin =  postorderBegin;
        int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
        // 右后序区间，左闭右开[rightPostorderBegin, rightPostorderEnd)
        int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
        int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素，已经作为节点了

        cout << "----------" << endl;
        cout << "leftInorder :";
        for (int i = leftInorderBegin; i < leftInorderEnd; i++) {
            cout << inorder[i] << " ";
        }
        cout << endl;

        cout << "rightInorder :";
        for (int i = rightInorderBegin; i < rightInorderEnd; i++) {
            cout << inorder[i] << " ";
        }
        cout << endl;

        cout << "leftpostorder :";
        for (int i = leftPostorderBegin; i < leftPostorderEnd; i++) {
            cout << postorder[i] << " ";
        }
        cout << endl;

        cout << "rightpostorder :";
        for (int i = rightPostorderBegin; i < rightPostorderEnd; i++) {
            cout << postorder[i] << " ";
        }
        cout << endl;

        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  postorder, leftPostorderBegin, leftPostorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);

        return root;
    }
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if (inorder.size() == 0 || postorder.size() == 0) return NULL;
        return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
    }
};

力扣的代码

感觉官方题解和卡哥的优化代码差不多的思路。官方题解相对来说更简洁。

作者：力扣官方题解
链接：https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/solutions/426738/cong-zhong-xu-yu-hou-xu-bian-li-xu-lie-gou-zao-14/
来源：力扣（LeetCode）著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。


class Solution {
	int postIndex;
	unordered_map<int, int>indexMap;//存中序遍历的数组和下标的键值对。

public:
	TreeNode* helper(int inLeft, int inRight, vector<int>& inorder, vector<int>& postorder) {
		// 如果这里没有节点构造二叉树了，就结束
		if (inLeft > inRight) return nullptr;

		// 选择 postIndex 位置的元素作为当前子树根节点
		int root_val = postorder[postIndex];
		TreeNode* root = new TreeNode(root_val);

		// 根据 root 所在位置分成左右两棵子树
		int index = indexMap[root_val];//根节点的下标（中序遍历的）

		// 下标减一
		postIndex--;//指向分隔开的 右子树的根节点的下标（后序遍历的）

		// 构造右子树
		root->right = helper(index + 1, inRight, inorder, postorder);  //左闭右闭
		root->left = helper(inLeft, index - 1, inorder, postorder);    //左闭右闭
		return root;
	}

	TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
		// 从后序遍历的最后一个元素开始
		postIndex = postorder.size() - 1;

		// 建立（元素，下标）键值对的哈希表
		int idx{ 0 };
		for (const auto& val : inorder) {
			indexMap[val] = idx++;
		}

		return helper(0, postIndex, inorder, postorder);
	}
};