【面试题】

一个社交APP, 它的新增用户次日留存、7日留存、30日留存分别是52%、25%、14%。

请模拟出来，每天如果日新增6万用户，那么第30天，它的日活数会达到多少？请使用Excel进行分析。

【分析思路】

第1日(次日)留存用户数=第1日新增用户数*次日留存率

第2日活跃用户数=第2日新增用户数+第1日留存用户数

第3日活跃用户数=第3日新增用户数+第2日留存用户数（第2日新增用户数*第2日留存率）+第1日留存用户数

...

第30日活跃用户数=第30日新增用户数+第29日留存用户数+第28日留存用户数+...+第1日留存用户数

也就是，

第30日活跃用户数=1-29日每天的留存用户数（第1日留存用户数+第2日留存用户数+...+第29日留存用户数）+第30日新增用户数

现在只需要计算出1-29日每天的留存用户数就可以了，而第N日的留存用户数=第N日新增用户数（6万）*第N日留存率。所以现在的问题是需要知道每天的留存率是多少。

那么，问题就来了。题目只有3个留存率（新增用户次日留存、7日留存、30日留存分别是52%、25%、14%）。

如何根据已有的几个留存率去预测剩下那些天的留存率呢？

很简单，用excel 1分钟就能搞定。

1.用现有的数据做散点图

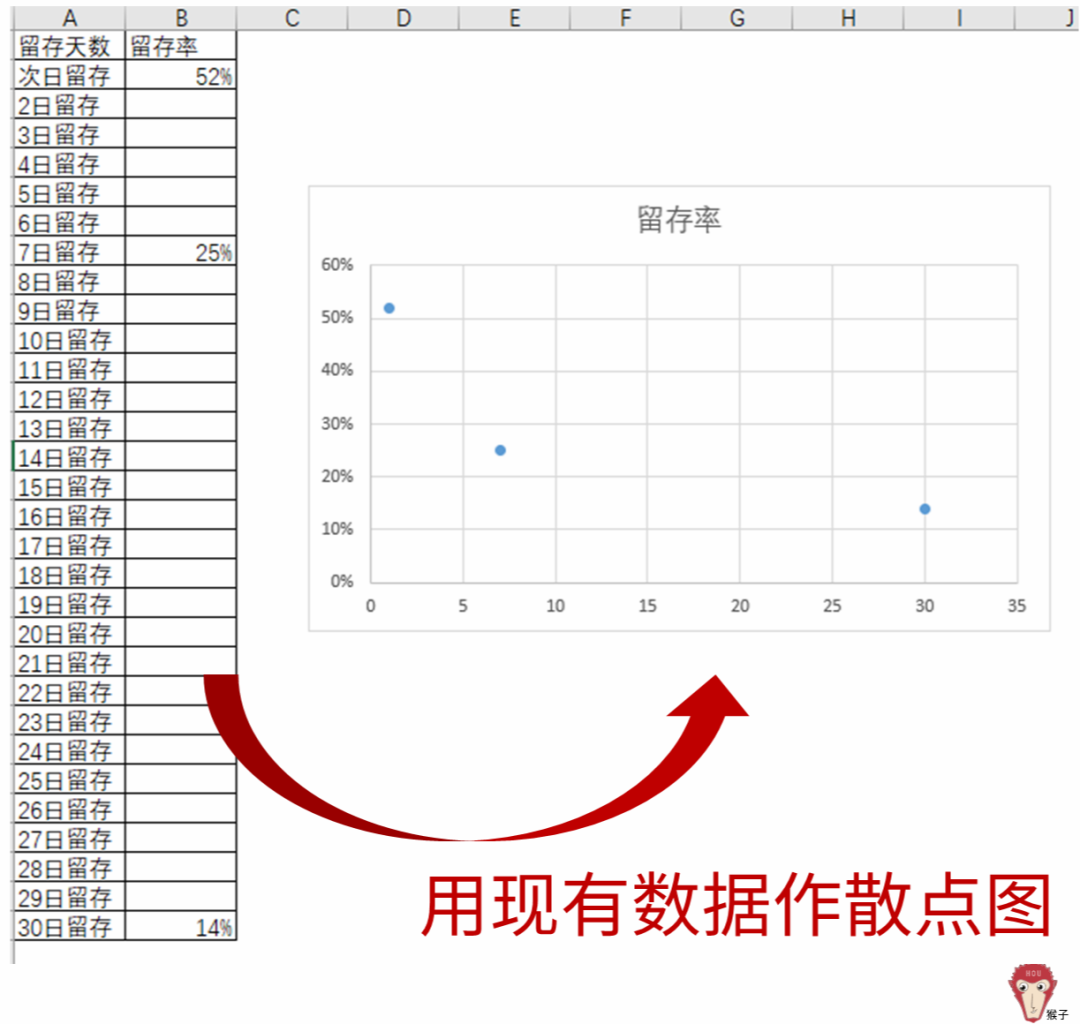
2.对散点图添加趋势线

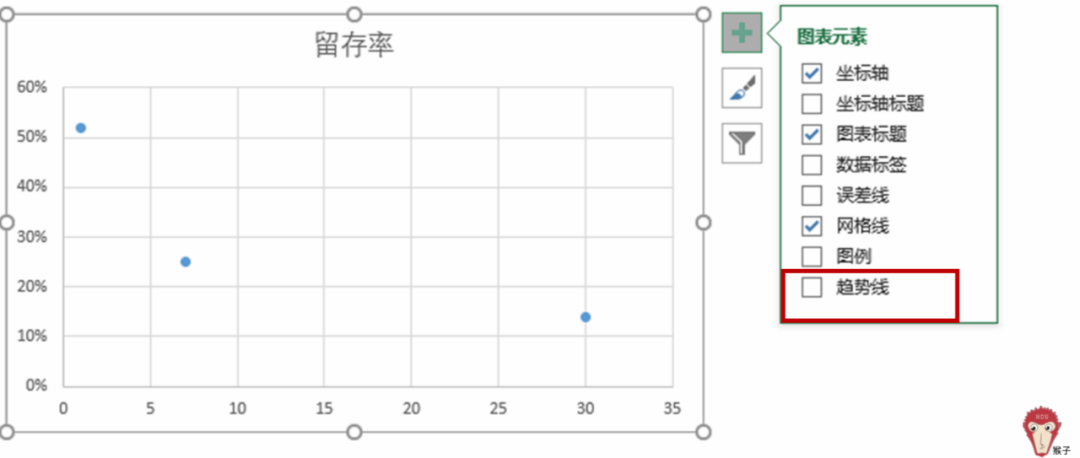
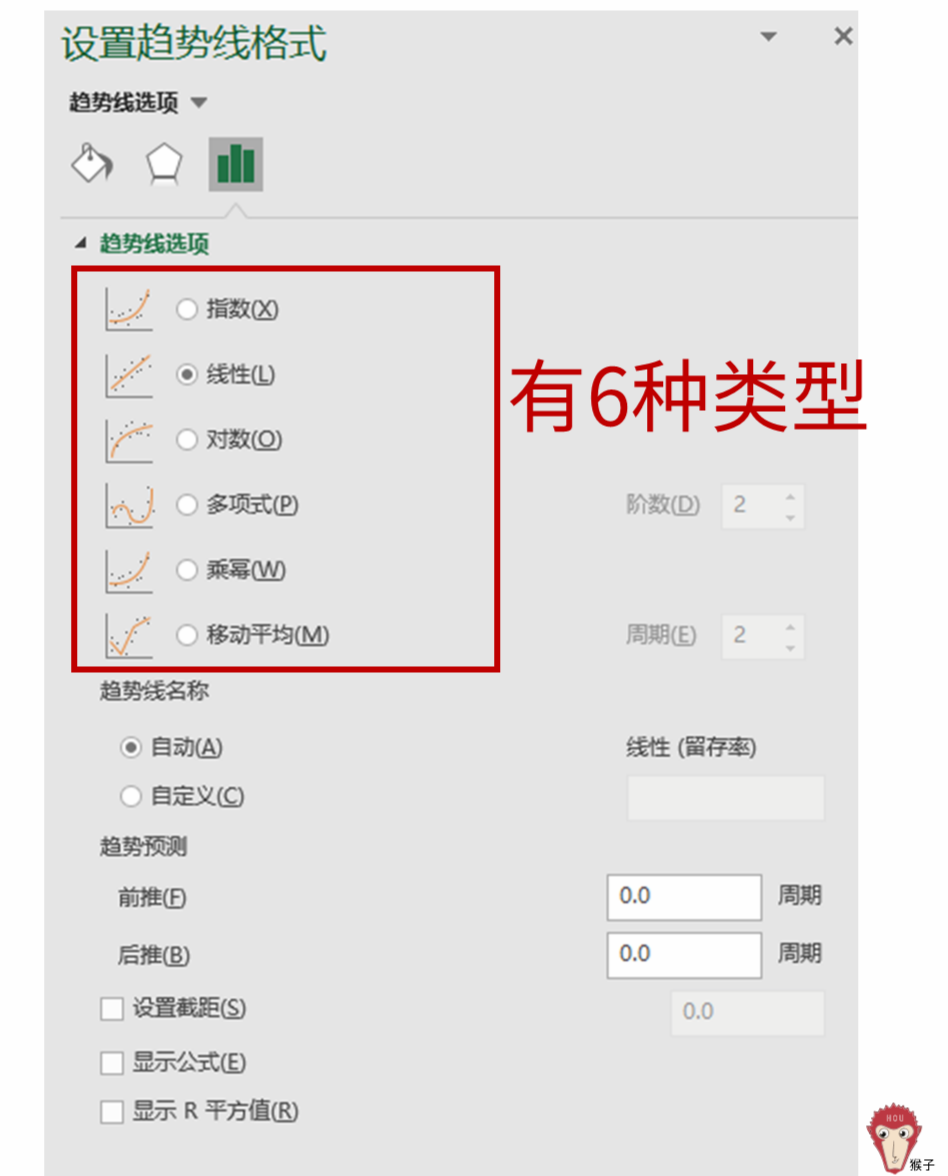
趋势线有以下几种类型，应该添加哪一类型的趋势线呢？

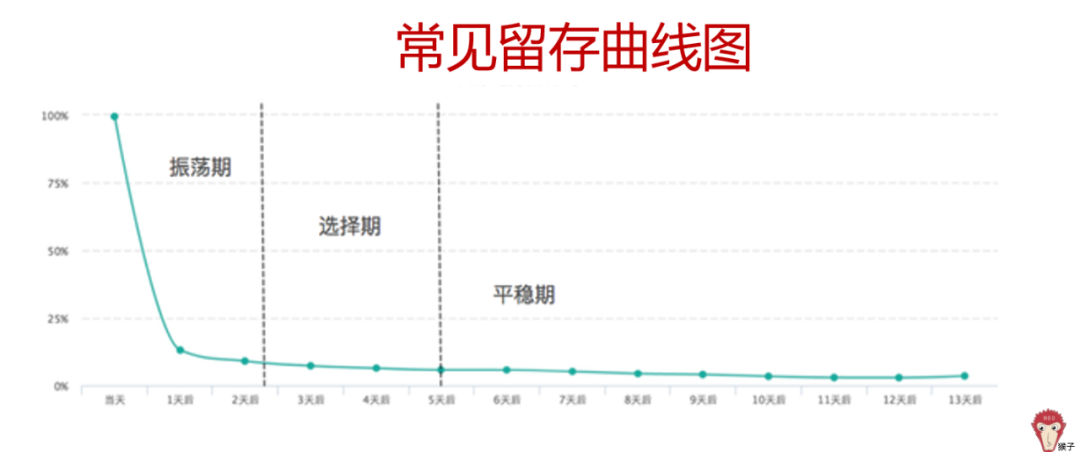
一般来说，正常的留存曲线是一开始快速下降，然后开始缓慢下降，最后逐步平稳的曲线。

所以，留存曲线的形状会类似于下图：初始在震荡期快速下降；选择期开始缓慢下降；过了选择期就是平稳期，留存率会进入一个相对稳定的阶段。

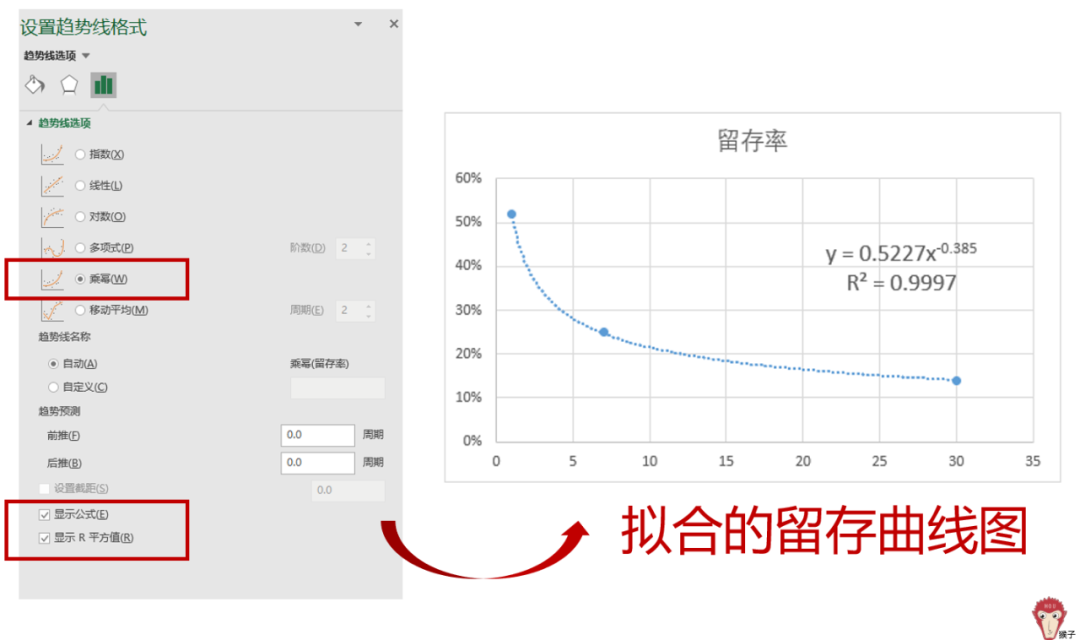
这种留存曲线的形状和乘幂函数十分接近，所以，在这里我们用乘幂函数来对留存曲线进行拟合。同时勾选“显示公式”和“显示R平方值”。最终得到了如下曲线，函数公式为y = 0.5227x^-0.385，R² = 0.9997，可以看到拟合后的幂函数的形状和上图的留存曲线的形状几乎一样。

拓展：

你肯定想知道这个趋势线的可靠性有多大？

这就涉及到趋势线的 R 平方值。R 平方值是介于 0 和 1 之间的数值。当趋势线的 R 平方值为 1 或者接近 1 时，趋势线最可靠。如案例演示中，R的平方值达到了0.9997，因此可以说这条趋势线可靠性非常大。

要获得最精确的预测，为数据选择最合适的趋势线非常重要。

那么，什么情况下选用什么样的趋势线呢？

指数：指数趋势线适用于速度增加越来越快的数据。

线性：线性趋势线是适用于简单线性数据集合的最佳拟合直线。如果数据点的构成的趋势接近于一条直线，则数据应该接近于线性。线性趋势线通常表示事件以恒定的比率增加或减少。

对数：如果数据一开始的增加或减小的速度很快，但又迅速趋于平稳，那么对数趋势线则是最佳的拟合曲线。

多项式:多项式趋势线是数据波动较大时使用的曲线。

乘幂：乘幂趋势线是一种适用于以特定速度增加的曲线。但是如果数据中有零或负数，则无法创建乘幂趋势线。

移动平均：移动平均趋势线用于平滑处理数据中的微小波动，从而更加清晰地显示了数据的变化的趋势。（在股票、基金、汇率等技术分析中常用）

3.计算第n天留存率

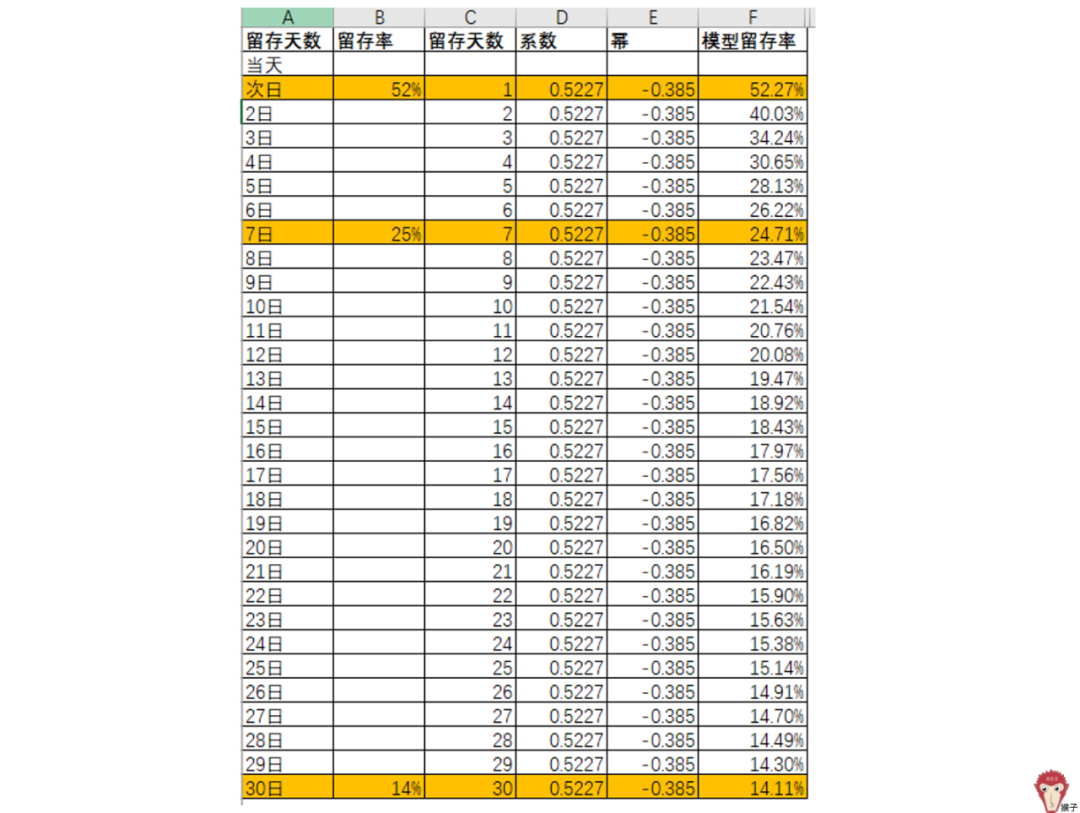
拟合出留存曲线后， 我们就可以根据拟合的函数公式（y = 0.5227x^-0.385）去计算次日到30日的留存率。

也就是把x=1,x=2…x=30,分别代入函数公式，这里可以借助Excel的power幂函数，求出结果。如下图，可以看到按照模型函数公式计算出来的留存率，即模型留存率与给定的留存率几乎完全一致（黄色的行）。

4.计算30天后日活数

通过上面的步骤，我们已经得到了每天的留存率。接下来我们就可以计算第30天的日活用户数有多少。

第1日(次日)留存用户数=第1日新增用户数*次日留存率

第2日活跃用户数=第2日新增用户数+第1日留存用户数

第3日活跃用户数=第3日新增用户数+第2日留存用户数（第2日新增用户数*第2日留存率）+第1日留存用户数

...

第30日活跃用户数=第30日新增用户数+第29日留存用户数+第28日留存用户数+...+第1日留存用户数

也就是，

第30日活跃用户数=1-29日每天的留存用户数（第1日留存用户数+第2日留存用户数+...+第29日留存用户数）+第30日新增用户数

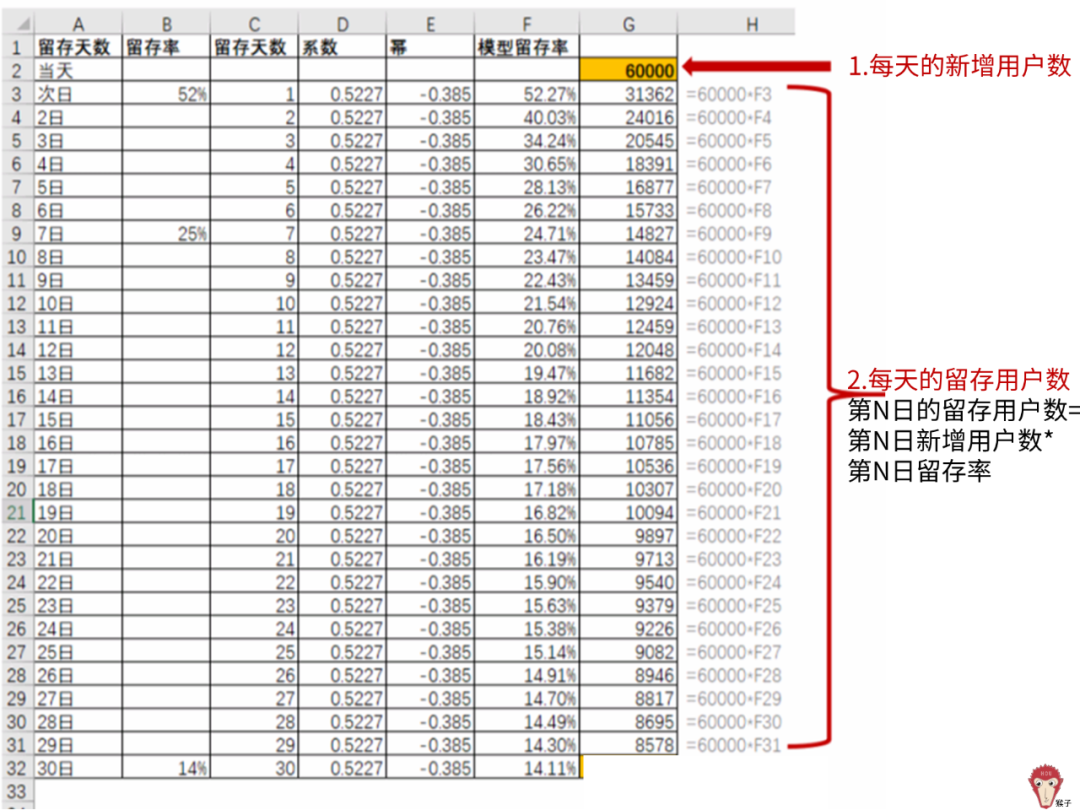
（1）在下图Excel步骤1的地方是题目的设定，每天固定新增用户数为6万

在下图步骤2的地方算出1-29日每天的留存用户数，也就是第N日新增用户数（6万）*第N日留存率（F列对应的留存率）。

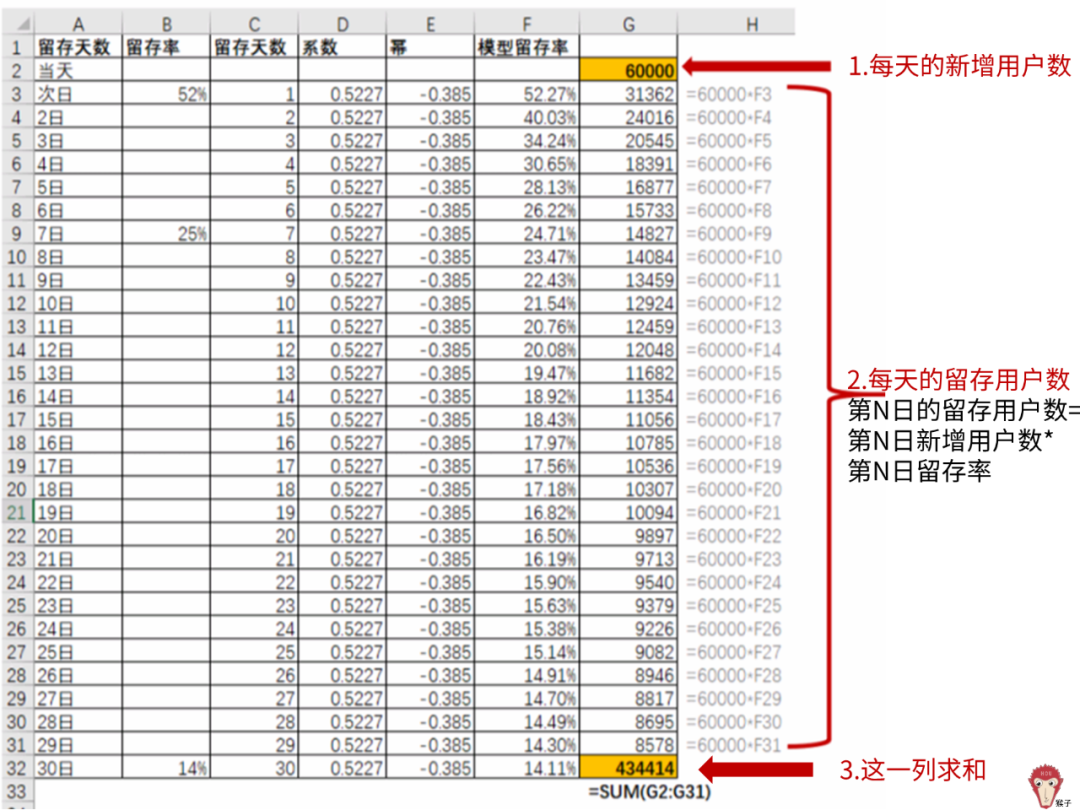
（3）下图步骤3将这一列的值求和，就是第30日活跃用户数=1日-29日每天的留存用户数+第30日新增用户数。

5.总结

Excel里进行预测分析的2种办法：

1）时间序列数据如何预测？用预测工作表

2）其他数据如何预测？先画散点图，然后添加趋势线和公式

快来学职场晋级技巧：如何做出老板喜欢的图表！点击看视频教学：‍‍‍‍‍‍‍‍‍‍‍‍

 ⬇️点击「阅读原文」

 免费报名 数据分析训练营