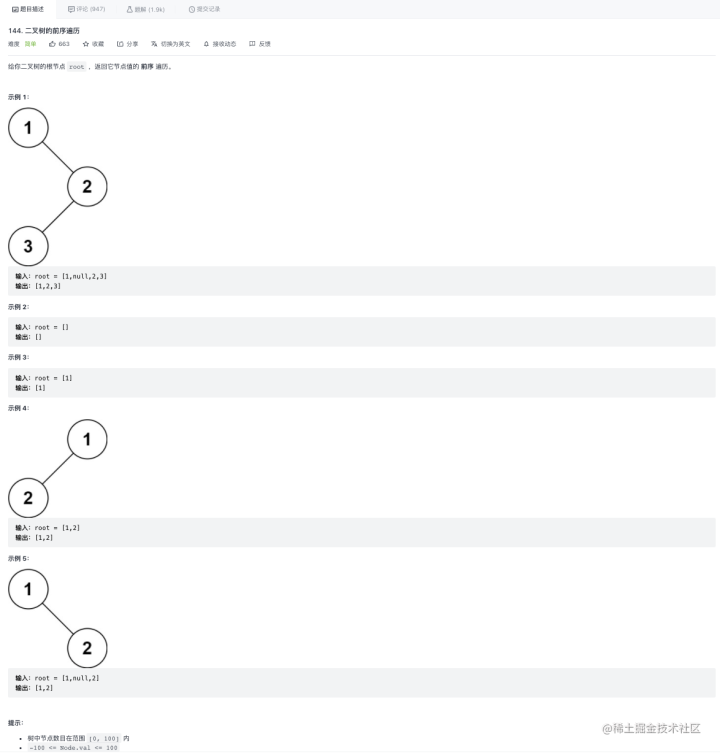
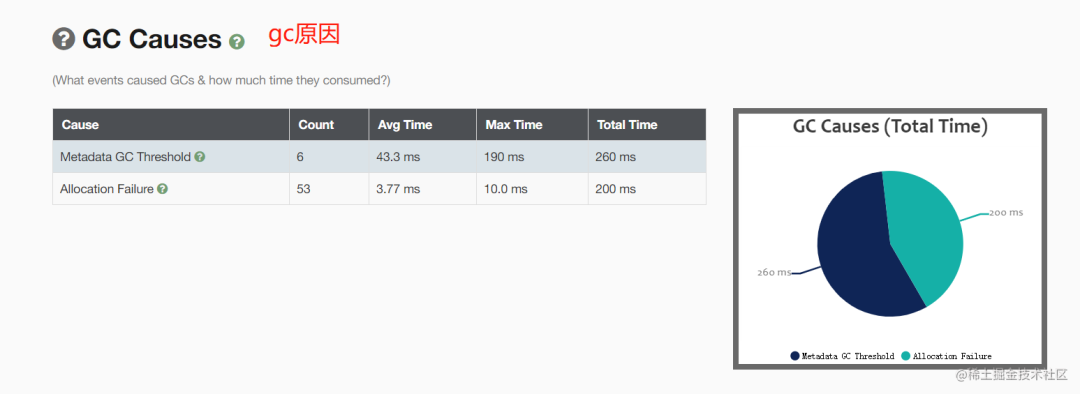
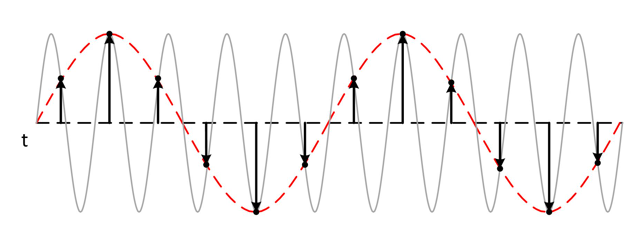
【问题】
Is there a way to use the $map operator in a regular Mongo document query (or aggregate \$match which I believe is the same thing).
What I’m trying to do is thus: Given an set of sets, return the document if any of the sets is a subset of a parameter.
Example:
Let’s say I have three documents:
{x : [ [“A”,“B”] ] }
{x : [ [“A”, “D”] ] }
{x : [ [“A”,“B”], [“A”,“D”] ] }
and I have an array
auths = [“A”,“B”,“C”]I want to run a query where I get back the first and third documents because both contain the set [“A”,“B”] which is a subset of auths, but not the second document because its only set contains D which is not in the set of auths
If I were doing this in a $redact pipeline I could do this with something along the lines of:
{“$anyElementTrue” : {
“$map” : {
“input”: “$x”,
“as”: “s”,
“in”: {“$setIsSubset”: [“$$s”, auths] }
}
}}but when I try to run this as a query I get
BadValue unknown top level operator: $anyElementTrue
【回答】
直接使用 Mongodb 的 API 应该可以实现这个需求,但会比较繁琐,也可以考虑用 SPL 解决:
A | |
1 | =mongo_open(“mongo://localhost:27017/local?user=test&password=test”) |
2 | =mongo_shell(A1,”test36.find()”) |
3 | =[“a”,“b”,“c”] |
4 | =A2.select(.au.pselect(A3.pos())>0) |
5 | >mongo_close(A1) |
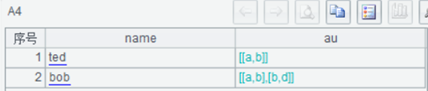
A2:
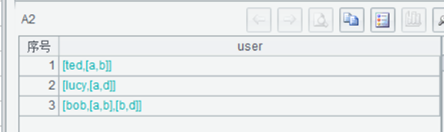
A3:对照序列
A4:对照 A2 每条记录的 au 是不是 A3 的子集,如果是就查出来






![洛谷千题详解 | P1031 [NOIP2002 提高组] 均分纸牌【C/C++、pascal、Java语言】](https://img-blog.csdnimg.cn/a3112a19885547179130c9ee445fc4d4.png)