1. 剪绳子

原题链接：
剑指 Offer 14- I. 剪绳子 - 力扣（LeetCode）https://leetcode.cn/problems/jian-sheng-zi-lcof/

1.1 题目描述

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

1.2 基础知识

1.2.1 动态规划

如果题目中是求一个问题的最优解（通常是最大值和最小值），而且该问题能够分解成若干个子问题，并且子问题之间还有重叠的更小的子问题，就可以考虑用动态规划来解决这个问题。

应用动态规划求解问题的特点1：能够把大问题分解成小问题并且分解后的小问题也存在最优解。

例如在本题中，我们不妨把长度为n的绳子剪成若干段后得到的乘积的最大值定义为函数f(n)。假设我们第一次剪在长度为i的位置，于是绳子变成了i和n-i两段。我们想要求到该题的最优解f(n)，那么同样要用最优化的方法把长度为i和n-i的两段剪成若干段，使得他们各自剪出的每段绳子的长度乘积最大。

于是我们便得到了应用动态规划求解问题的特点2：整体问题的最优解是依赖于各个子问题的最优解。

应用动态规划求解问题的特点3：我们把大问题分解成若干个小问题，这些小问题之间还有互相重叠的更小的子问题。假设绳子的初始长度为10，我们可以把绳子剪成4和6的两段，也就是f(4)和f(6)都是f(10)的子问题。接下来分别求解这两个子问题.我们把长度为4 的绳子剪成长度均为2的两段，即f(2)是f(4)的子问题。相似地，我们可以把长度为6的绳子剪成长度分别为2和4的两段，即f(2)和f(4)都是f(6)的子问题。于是我们便可以发现f(2)是f(4)和f(6)公共的子问题。

由于子问题在分解大问题的过程中重复出现，为了避免重复求解子问题，我们采用从下往上的顺序先计算小问题的最优解并储存下来，再以此为基础求取大问题的最优解。从上往下分析问题，从下往上求解问题，这便是应用动态规划求解问题的特点4。我们通常把已经解决的子问题的最优解存储在一维或二维数组中，并且把子问题的最优解组合起来逐步解决大问题。

在运用动态规划的时候，我们每一步都可能面临若干个选择。例如在求解本题时，剪第一刀有n-1个选择。由于我们不知道剪在哪个位置才是最优解，只能把所有能剪的位置（1到n-1）尝试一遍。

1.2.2 贪婪算法

贪婪算法与动态规划不同。我们应用贪婪算法解决问题时，每一步都可以做一个贪婪的选择，基于这个选择我们能够确定最优解。对于本题这个贪婪的选择就是3（解题时证明），当绳子的长度大于等于4时，则每次剪出一段长度为3 的绳子，以此类推，直到剩余绳子长度小于3 。为什么这样的贪婪选择能够的到最优解？这便需要数学的方式来证明贪婪选择是正确的。

1.3 思路一：动态规划

对于长度为n的绳子，同样假设绳子剪成若干段后得到的乘积的最大值定义为函数f(n)，我们在其长度为i（1<i<n）的地方剪第一刀时，得到长度为i和长度为n-i的两段绳子。对于长度为n-i的绳子我们有两种选择：

选择一：对长度为n-i的绳子不继续往下剪，于是得到长度乘积：i * (n - i)。

选择二：对长度为n-i的绳子继续往下剪，于是得到长度乘积：i * f(n - i)。

接下来便可得到f(n) = max[ i * (n - i), i * f(n - i) ]，i = 1, 2, 3, ....... , n - 1。

同样地我们不知道那里才是最优解，所以需要将i = 1，到i = n - 1 都尝试一遍。

该解题方法时间复杂度O(N*N)，空间复杂度O(N)。

int cuttingRope(int n){
    //开辟空间存储结果
    int* ret = (int*)calloc(sizeof(int), n+1);
    int i,j;
    //题目要求至少剪一次所以从长度为2开始
    for(i=2;i<=n;i++)
    {
        int max = 0;
        //这里的i对应思路中的n，自下向上求解问题，从子问题的求解过程中逐步解决长度为n的结果
        for(j=1;j<i;j++)
        {
            //不清楚哪一次求得最优解，所以要将上一次的结果参与最大值的选择。
            max = fmax(max,fmax(j*(i-j),j*ret[i-j]));
        }
        //求得最优解之后将结果保存到一维数组
        ret[i] = max;
    }
    return ret[n];
}

1.4 思路二：贪婪算法

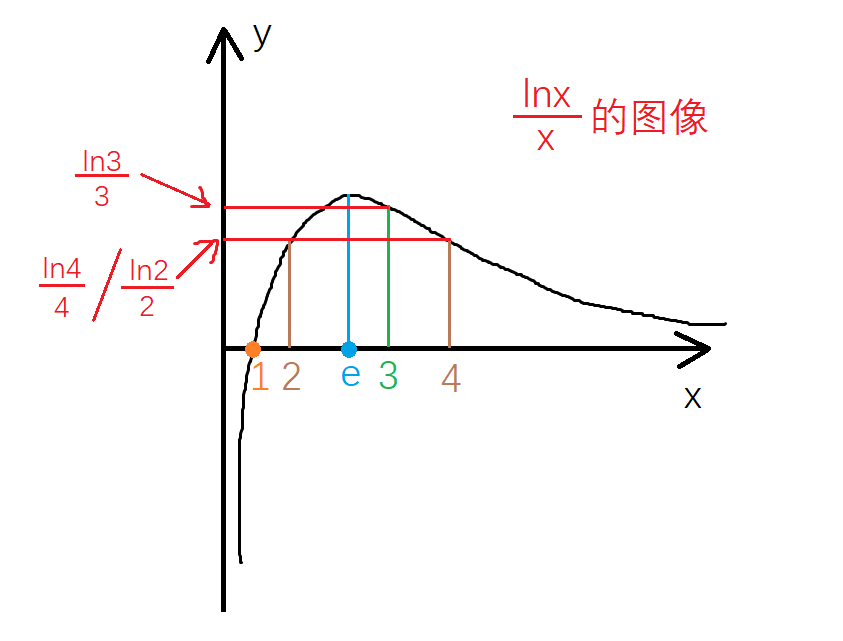
因为我们的贪婪选择是3，而题目要求至少剪一次，故当n<=3时不可用该方法计算，直接返回即可：

n = 3，最优解：2

n = 2，最优解：1

n = 1，最优解：0

该解题方法时间复杂度O(1)，空间复杂度O(1)。

int cuttingRope(int n){
    if(n<=3)
    {
        return n-1;
    }
    int times = n / 3;
    int mod = n % 3;
    if(mod == 0)
    {
        return (int)pow(3,times);
    }
    else if(mod == 1)
    {
        return (int)pow(3,times-1)*2*2;
    }
    else
    {
        return (int)pow(3,times)*2;
    }

}

1.5 思路一的优化

有了贪婪算法，我们就可以对思路一进行优化啦，将绳子剪成3段是贪婪选择，所以当我们用此公式来计算最优解时f(n) = max[ i * (n - i), i * f(n - i) ]，i = 1, 2, 3, ....... , n - 1。i >=4 就不需要计算啦，因为贪婪选择是3嘛，至于i = 1时,就更好想了，肯定不是最优解。

所以公式可以进行化简：f(n) = max{ max[ 2* (n - 2), 2 * f(n - 2) ], max[ 3 * (n - 3), 3 * f(n - 3) ] }。

该解题方法的时间复杂度为O(N)，空间复杂度为O(n)。

int cuttingRope(int n)
{
    int* ret = (int*)calloc(sizeof(int), n+1);
    ret[2] = 1;
    int i=0;
    for(i=3;i<=n;i++)
    {
        int max = fmax(fmax(2*(i-2), 2*ret[i-2]), fmax(3*(i-3),3*ret[i-3]));
        ret[i]=max;
    }
    return ret[n];
}