文章目录
- 无约束优化:Hessian-Free Optimization 拟牛顿类算法(BFGS,L-BFGS)
- 为什么要用拟牛顿算法
- 割线方程
- 严格凸且光滑函数的BFGS算法
- 非凸但光滑函数的BFGS算法
- L-BFGS算法
- 非凸非光滑函数的BFGS算法
- 参考文献
无约束优化:Hessian-Free Optimization 拟牛顿类算法(BFGS,L-BFGS)
为什么要用拟牛顿算法
前情提要:
无约束优化:线搜索最速下降
无约束优化:修正阻尼牛顿法
牛顿类算法需要计算Hessian矩阵或者通过一些修正方法计算类Hessian矩阵并将其储存,然后求解Hessian矩阵的逆或者解线性方程组 M d = − ∇ f ( x ) M d=-\nabla f(\boldsymbol{x}) Md=−∇f(x)确定搜索方向。然而对于大规模问题,计算Hessian矩阵或者类Hessian矩阵的代价很大,而且还需要计算一个大规模Hessian矩阵的逆或者求解大规模线性方程组,这样计算量大,程序的时间复杂度高。
对于非凸问题,修正阻尼牛顿法虽然可以构造严格正定且条件数低的类Hessian矩阵 M M M保证牛顿法搜索方向的有效性,但存在矩阵计算量大、存储麻烦、求解大规模线性方程组慢的问题。
拟牛顿类算法可以解决上述问题,它能够在每一步以较小的计算代价生成近似Hessian矩阵(或者Hessian矩阵的逆)的正定对称阵,在拟牛顿的条件下优化目标函数并具有超线性收敛性质(super-linear performance),不同的构造方法就产生了不同的拟牛顿法。简单来说,拟牛顿类算法就是一种既想利用函数高阶信息,又不想计算Hessian矩阵的Hessian-Free优化方法。
割线方程
已知牛顿法本质上是对目标函数
f
(
x
)
f(x)
f(x)在迭代点
x
k
x_k
xk处做二阶近似求解得到。假设
f
(
x
)
f(x)
f(x)二阶连续可微,对
∇
f
(
x
)
\nabla f(\boldsymbol{x})
∇f(x)在点
x
k
+
1
x^{k+1}
xk+1处一阶泰勒近似,得
∇
f
(
x
)
=
∇
f
(
x
k
+
1
)
+
∇
2
f
(
x
k
+
1
)
(
x
−
x
k
+
1
)
+
O
(
∥
x
−
x
k
+
1
∥
2
)
\nabla f(x)=\nabla f\left(x^{k+1}\right)+\nabla^2 f\left(x^{k+1}\right)\left(x-x^{k+1}\right)+\mathcal{O}\left(\left\|x-x^{k+1}\right\|^2\right)
∇f(x)=∇f(xk+1)+∇2f(xk+1)(x−xk+1)+O(
x−xk+1
2)
令
x
=
x
k
x=x^k
x=xk,且
Δ
x
=
x
k
+
1
−
x
k
\Delta x=x^{k+1}-x^k
Δx=xk+1−xk为点差,
Δ
g
=
∇
f
(
x
k
+
1
)
−
∇
f
(
x
k
)
\Delta g=\nabla f\left(x^{k+1}\right)-\nabla f\left(x^k\right)
Δg=∇f(xk+1)−∇f(xk)为梯度差,得
∇
2
f
(
x
k
+
1
)
Δ
x
+
O
(
∥
Δ
x
∥
2
)
=
Δ
g
\nabla^2 f\left(x^{k+1}\right) \Delta x+\mathcal{O}\left(\left\|\Delta x\right\|^2\right)=\Delta g
∇2f(xk+1)Δx+O(∥Δx∥2)=Δg
现忽略高阶项
O
(
∥
Δ
x
∥
2
)
\mathcal{O}\left(\left\|\Delta x\right\|^2\right)
O(∥Δx∥2),只希望近似Hessian矩阵的
H
k
+
1
H^{k+1}
Hk+1满足方程
H
k
+
1
Δ
x
=
Δ
g
H^{k+1} \Delta x=\Delta g
Hk+1Δx=Δg
或其逆矩阵
B
k
+
1
B^{k+1}
Bk+1满足
B
k
+
1
Δ
g
=
Δ
x
B^{k+1} \Delta g=\Delta x
Bk+1Δg=Δx
上述两个方程即称为割线方程。
实际应用中基于 B k B^{k} Bk的拟牛顿法更加实用,因为根据 B k B^k Bk计算下降方向 d k d^k dk不需要求解线性方程组,只需要做矩阵相乘运算即可,对于大规模问题可以极大简化计算量。下面的问题就是如何找到满足割线条件的近似矩阵 B k B^k Bk并进行迭代更新。
严格凸且光滑函数的BFGS算法
BFGS算法推导过程可参考:牛顿法与拟牛顿法学习笔记(四)BFGS 算法,逻辑回归模型及LBFGS的Sherman Morrison(SM) 公式推导
对于严格凸且光滑的函数,采用如下BFGS算法。核心的BFGS更新公式为
B
k
+
1
=
(
I
−
Δ
x
Δ
g
T
Δ
g
T
Δ
x
)
B
k
(
I
−
Δ
g
Δ
x
T
Δ
g
T
Δ
x
)
+
Δ
x
Δ
x
T
Δ
g
T
Δ
x
B^{k+1}=\left(I-\frac{\Delta x \Delta g^T}{\Delta g^T \Delta x}\right) B^k\left(I-\frac{\Delta g \Delta x^T}{\Delta g^T \Delta x}\right)+\frac{\Delta x \Delta x^T}{\Delta g^T \Delta x}
Bk+1=(I−ΔgTΔxΔxΔgT)Bk(I−ΔgTΔxΔgΔxT)+ΔgTΔxΔxΔxT
其中,
B
0
=
I
,
Δ
x
=
x
k
+
1
−
x
k
,
Δ
g
=
∇
f
(
x
k
+
1
)
−
∇
f
(
x
k
)
B^0=I, \Delta x=x^{k+1}-x^k, \Delta g=\nabla f\left(x^{k+1}\right)-\nabla f\left(x^k\right)
B0=I,Δx=xk+1−xk,Δg=∇f(xk+1)−∇f(xk)
从该更新公式可以看出:
- 完全不需要得到函数二阶信息;
- 不需要求解线性方程组,只需要矩阵相乘 B ∗ Δ g = Δ x B^{*} \Delta g=\Delta x B∗Δg=Δx, B ∗ B^* B∗是 H − 1 H^{-1} H−1的最佳估计;
- 对于严格凸且光滑函数而言,该更新公式可严格保证 B k + 1 B^{k+1} Bk+1在迭代更新过程中保持对称正定,下面详述证明过程;
- 在一定程度上降低了存储复杂度。

证:对于严格凸且光滑函数而言,该更新公式可严格保证 B k + 1 B^{k+1} Bk+1在迭代更新过程中保持对称正定
证明:由凸函数的二阶条件可知,若
f
(
x
)
f(x)
f(x)严格凸,表明梯度函数
∇
f
(
x
)
\nabla f(\boldsymbol{x})
∇f(x)单调递增,
⟨
x
k
+
1
−
x
k
,
∇
f
(
x
k
+
1
)
−
∇
f
(
x
k
)
⟩
>
0
\langle x^{k+1}-x^k,\nabla f(\boldsymbol{x^{k+1}})-\nabla f(\boldsymbol{x^k}) \rangle >0
⟨xk+1−xk,∇f(xk+1)−∇f(xk)⟩>0,即存在如下条件
Δ
g
T
Δ
x
>
0
\Delta g^T \Delta x>0
ΔgTΔx>0
将该条件称为曲率条件,下面推导满足曲率条件即可保证BFGS更新过程中的正定性。



因此,对于严格凸且光滑的函数而言,BFGS算法流程如上图所示。
非凸但光滑函数的BFGS算法
毋容置疑,要求函数严格凸且光滑的BFGS算法局限性很大,该方法只是用来引入BFGS更新公式和分析其迭代过程中的重要性质,实际问题基本不用。下面分析非凸但光滑函数的BFGS算法。
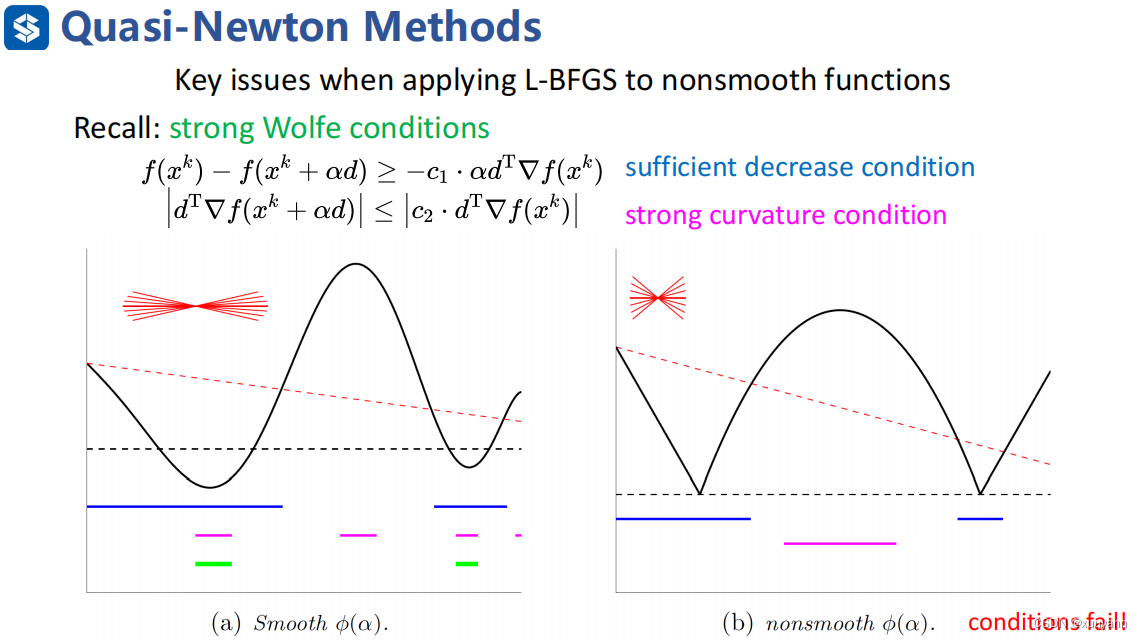
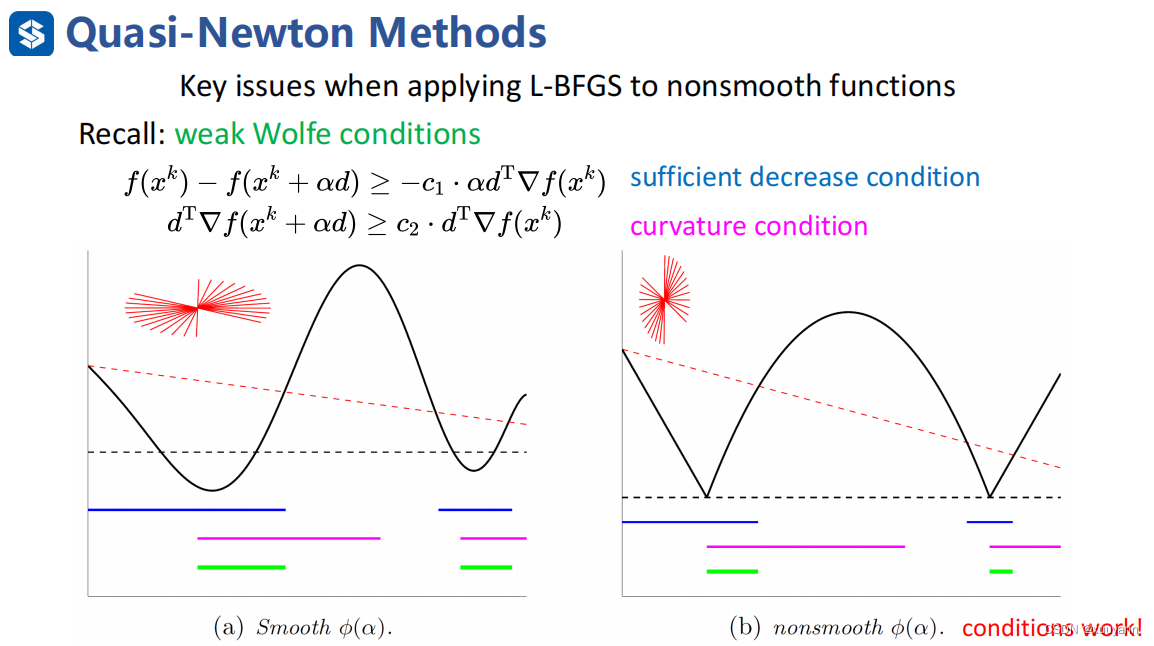
对于非凸但光滑函数,采用Wolfe准则计算步长进行线搜索即可保证满足曲率条件 Δ g T Δ x > 0 \Delta g^T \Delta x>0 ΔgTΔx>0。有两种Wolfe条件,一种是weak Wolfe条件,另一种为strong Wolfe条件,如下图所示,详细解释可见博客:无约束优化:线搜索最速下降。strong Wolfe就是在weak Wolfe的基础上对第二个条件加了绝对值,减少了一部分迭代范围,可起到一定的震荡抑制作用。
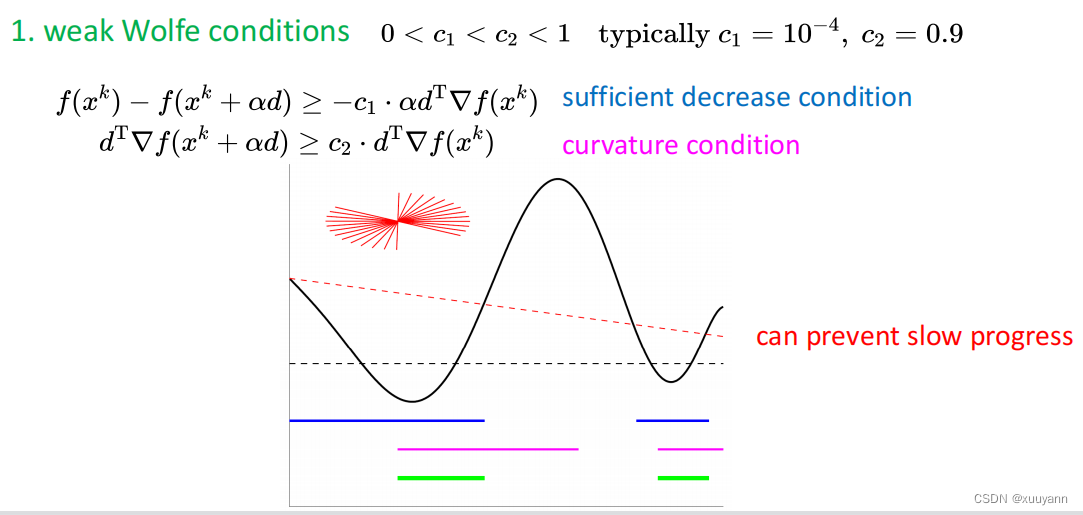
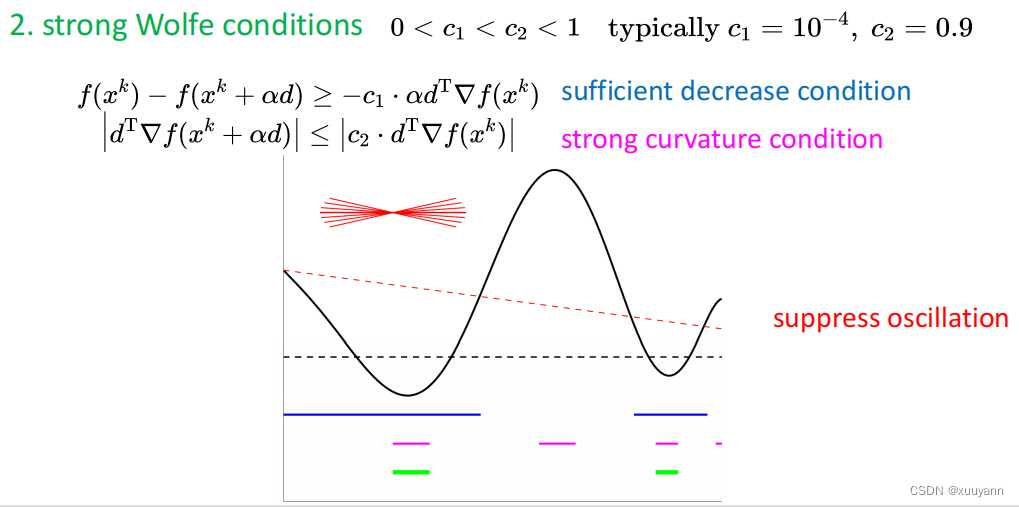
为什么说"对于非凸但光滑函数,采用Wolfe准则计算步长进行线搜索即可保证满足曲率条件 Δ g T Δ x > 0 \Delta g^T \Delta x>0 ΔgTΔx>0"?
根据weak Wolfe第二个条件有
d
T
∇
f
(
x
k
+
α
d
)
≥
c
2
⋅
d
T
∇
f
(
x
k
)
d^{\mathrm{T}} \nabla f\left(x^k+\alpha d\right) \geq c_2 \cdot d^{\mathrm{T}} \nabla f\left(x^k\right)
dT∇f(xk+αd)≥c2⋅dT∇f(xk),两边同时减去
d
T
∇
f
(
x
k
)
d^{\mathrm{T}} \nabla f\left(x^k\right)
dT∇f(xk),
d
=
Δ
x
=
x
k
+
1
−
x
k
d=\Delta x = x^{k+1}-x^k
d=Δx=xk+1−xk,有
Δ
g
T
Δ
x
⩾
(
c
2
−
1
)
∇
f
(
x
k
)
T
Δ
x
>
0
\Delta g^{\mathrm{T}} \Delta x \geqslant\left(c_2-1\right) \nabla f\left(x^k\right)^{\mathrm{T}} \Delta x>0
ΔgTΔx⩾(c2−1)∇f(xk)TΔx>0
这是因为
c
2
<
1
c_2<1
c2<1以及
Δ
x
\Delta x
Δx是下降方向,
∇
f
(
x
k
)
T
Δ
x
<
0
\nabla f\left(x^k\right)^{\mathrm{T}} \Delta x <0
∇f(xk)TΔx<0。满足strong Wolfe条件肯定满足weak Wolfe条件,因此存在如下逻辑关系:

Wofle条件并不能保证BFGS算法的全局收敛性,Cautious update(Li and Fukushima 2001)可以解决这个问题。该条件的加持,可以严格保证Wolfe+BFGS在任意非凸但光滑函数上能稳定收敛,但一般在工程上可以不加该条件,因为对于一般的工程问题Wolfe+BFGS都还是可以收敛的,几乎没有不能收敛的情况。该条件也很简单,就是在BFGS更新公式前做个条件判断,如下图所示。

综上所述,Wolfe准则保证满足曲率条件,从而使得BFGS更新严格正定,Cautious update保证BFGS的全局收敛性。因此,对于非凸但光滑函数,BFGS算法流程如下所示。

L-BFGS算法
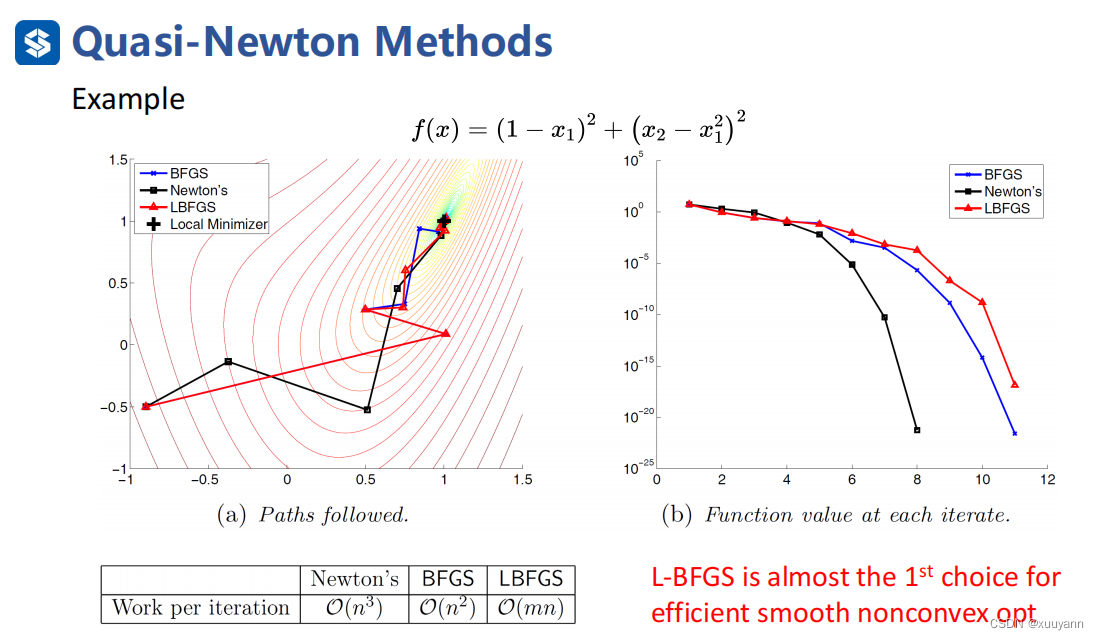
上述拟牛顿法虽然克服了计算Hessian矩阵的困难,但 B k B^k Bk是稠密矩阵,存储该类型矩阵需要消耗 O ( n 2 ) \mathcal{O}\left(n^2\right) O(n2)的内存,这还是不能适用于大规模问题。有限内存BFGS方法(L-BFGS)可以解决这一问题,可将时间复杂度降到 O ( m n ) \mathcal{O}\left(mn\right) O(mn),虽然迭代步长会增加,但单位步长的时间复杂度比牛顿法和原BFGS降低很多,程序运行的总时长会降低很多,因此对于光滑非凸函数而言,L-BFGS算法是首选优化算法。下面ppt中的 H k H^k Hk和 B k B^k Bk反过来了,理解起来没影响。






由下图可知,时间复杂度降到 O ( m n ) \mathcal{O}\left(mn\right) O(mn)。
可以结合matlab程序一起理解:L-BFGS 解优化问题
function [x, f, g, Out]= fminLBFGS_Loop(x, fun, opts, varargin)
%%%
% 从输入的结构体 |opts| 中读取参数或采取默认参数。
%
% * |opts.xtol| :主循环针对优化变量的停机判断依据
% * |opts.gtol| :主循环针对梯度范数的停机判断依据
% * |opts.ftol| :主循环针对函数值的停机判断依据
% * |opts.rho1| :线搜索标准 c1
% * |opts.rho2| :线搜索标准 c2
% * |opts.m| :L-BFGS 的内存对存储数
% * |opts.maxit| :主循环的最大迭代次数
% * |opts.storeitr| :标记是否记录每一步迭代的 x
% * |opts.record| :标记是否需要迭代信息的输出
% * |opts.itPrint| :每隔几步输出一次迭代信息
if ~isfield(opts, 'xtol'); opts.xtol = 1e-6; end
if ~isfield(opts, 'gtol'); opts.gtol = 1e-6; end
if ~isfield(opts, 'ftol'); opts.ftol = 1e-16; end
if ~isfield(opts, 'rho1'); opts.rho1 = 1e-4; end
if ~isfield(opts, 'rho2'); opts.rho2 = 0.9; end
if ~isfield(opts, 'm'); opts.m = 5; end
if ~isfield(opts, 'maxit'); opts.maxit = 1000; end
if ~isfield(opts, 'storeitr'); opts.storeitr = 0; end
if ~isfield(opts, 'record'); opts.record = 0; end
if ~isfield(opts,'itPrint'); opts.itPrint = 1; end
%%%
% 参数复制。
xtol = opts.xtol;
ftol = opts.ftol;
gtol = opts.gtol;
maxit = opts.maxit;
storeitr = opts.storeitr;
parsls.ftol = opts.rho1;
parsls.gtol = opts.rho2;
m = opts.m;
record = opts.record;
itPrint = opts.itPrint;
%%%
% 初始化和迭代准备,计算初始点处的信息。初始化迭代信息。
[f, g] = feval(fun, x , varargin{:});
nrmx = norm(x);
Out.f = f; Out.nfe = 1; Out.nrmG = [];
%%%
% 在 |storeitr| 不为 0 时,记录每一步迭代的 $x$。
if storeitr
Out.xitr = x;
end
%%%
% |SK| , |YK| 用于存储 L-BFGS 算法中最近的 m步的s( x 的变化量)和 y
% (梯度 g 的变化量)。
n = length(x);
SK = zeros(n,m);
YK = zeros(n,m);
istore = 0; pos = 0; status = 0; perm = [];
%%%
% 为打印每一步的迭代信息设定格式。
if record == 1
if ispc; str1 = ' %10s'; str2 = ' %6s';
else str1 = ' %10s'; str2 = ' %6s'; end
stra = ['%5s',str2,str2,str1, str2, str2,'\n'];
str_head = sprintf(stra, ...
'iter', 'stp', 'obj', 'diffx', 'nrmG', 'task');
str_num = ['%4d %+2.1e %+2.1e %+2.1e %+2.1e %2d\n'];
end
%% 迭代主循环
% 迭代最大步数 |maxit| 。当未达到收敛条件时,记录为超过最大迭代步数退出。
Out.msg = 'MaxIter';
for iter = 1:maxit
%%%
% 记录上一步迭代的结果。
xp = x; nrmxp = nrmx;
fp = f; gp = g;
%%%
% L-BFGS 双循环方法寻找下降方向。在第一次迭代时采用负梯度方向,之后便使用 L-BFGS 方法来
% 估计 d=-Hg。
if istore == 0
d = -g;
else
d = LBFGS_Hg_Loop(-g);
end
%%%
% 沿 L-BFGS 方法得到的下降方向做线搜索。调用函数 |ls_csrch| 进行线搜索,其参考了
% MINPACK-2 中的线搜索函数。
%
% 首先初始化线搜索标记 |workls.task| 为 1, |deriv| 为目标函数沿当前下降方向的方向导数。
% 通过线搜索寻找合适的步长 $\alpha_k$,使得以下条件满足:
%
% $$ \begin{array}{rl}
% f(x^k+\alpha_k d^k)&\hspace{-0.5em}\le
% f(x^k)+\rho_1\cdot\alpha_kg(x^k), \\
% |g(x^k+\alpha_kd^k)|&\hspace{-0.5em}\le \rho_2\cdot |g(x^k)|.
% \end{array} $$
%
% |ls_csrch| 每次调用只执行线搜索的一步,并用 |workls.task| 指示下一步应当执行的操作。
% 此处 |workls.task==2| 意味着需要重新计算当前点函数值和梯度等。具体的步长寻找过程比较复杂,可以参考相应文件。
%
% 直到满足线搜索条件时,退出线搜索循环,得到更新之后的 $x$。
workls.task =1;
deriv = d'*g;
normd = norm(d);
stp = 1;
while 1
[stp, f, deriv, parsls, workls] = ....
ls_csrch(stp, f, deriv , parsls , workls);
if (workls.task == 2)
x = xp + stp*d;
[f, g] = feval(fun, x, varargin{:});
Out.nfe = Out.nfe + 1;
deriv = g'*d;
else
break
end
end
%%%
% 对于线搜索得到的步长 $\alpha_k$,令 $s^k=x^{k+1}-x^k=\alpha_kd^k$,
% 则 $\|s^k\|_2=\alpha_k\|d^k\|_2$。计算 $\|s^k\|_2/\max(1,\|x^k\|_2)$
% 并将其作为判断收敛的标准。
nrms = stp*normd;
diffX = nrms/max(nrmxp,1);
%%%
% 更新 $\|x^{k+1}\|_2$, $\|g^{k+1}\|_2$,记录一步迭代信息。
nrmG = norm(g);
Out.nrmg = nrmG;
Out.f = [Out.f; f];
Out.nrmG = [Out.nrmG; nrmG];
if storeitr
Out.xitr = [Out.xitr, x];
end
nrmx = norm(x);
%%%
% 停机准则, |diffX| 表示相邻迭代步 $x$ 的相对变化, |nrmG| 表示当前 $x$ 处的梯度范数, $\displaystyle\frac{|f(x^{k+1})-f(x^k)|}{1+|f(x^k)|}$
% 用以表示函数值的相对变化。当前两者均小于阈值,或者第三者小于阈值时,认为达到停机标准,退出当前循环。
cstop = ((diffX < xtol) && (nrmG < gtol) )|| (abs(fp-f)/(abs(fp)+1)) < ftol;
%%%
% 当需要详细输出时,在(1)开始迭代时(2)达到收敛时(3)达到最大迭代次数或退出迭代时(4)每若干步,打印详细结果。
if (record == 1) && (cstop || iter == 1 || iter==maxit || mod(iter,itPrint)==0)
if iter == 1 || mod(iter,20*itPrint) == 0 && iter~=maxit && ~cstop
fprintf('\n%s', str_head);
end
fprintf(str_num, ...
iter, stp, f, diffX, nrmG, workls.task);
end
%%%
% 当达到收敛条件时,停止迭代,记为达到收敛。
if cstop
Out.msg = 'Converge';
break;
end
%%%
% 计算 $s^k=x^{k+1}-x^{k}$, $y^k=g^{k+1}-g^{k}$。
% 当得到的 $\|y^k\|$ 不小于阈值时,保存当前的 $s^k, y^k$,否则略去。利用 |pos|
% 记录当前存储位置,然后覆盖该位置上原来的信息。
ygk = g-gp; s = x-xp;
if ygk'*ygk>1e-20
istore = istore + 1;
pos = mod(istore, m); if pos == 0; pos = m; end
YK(:,pos) = ygk; SK(:,pos) = s; rho(pos) = 1/(ygk'*s);
%%%
% 用于提供给 L-BFGS 双循环递归算法,以指明双循环的循环次数。当已有的记录超过 $m$ 时,
% 则循环 $m$ 次。否则,循环次数等于当前的记录个数。 |perm| 按照顺序记录存储位置。
if istore <= m; status = istore; perm = [perm, pos];
else status = m; perm = [perm(2:m), perm(1)]; end
end
end
%%%
% 当从上述循环中退出时,记录输出。
Out.iter = iter;
Out.nge = Out.nfe;
%% L-BFGS 双循环递归算法
% 利用双循环递归算法,返回下一步的搜索方向即 $-Hg$。
% 初始化 $q$ 为初始方向,在 L-BFGS 主算法中,这一方向为负梯度方向。
function y = LBFGS_Hg_Loop(dv)
q = dv; alpha = zeros(status,1);
%%%
% 第一个循环, |status| 步迭代。( |status| 的计算见上,当迭代步足够大时为 $m$ )
% |perm| 按照顺序记录了存储位置。从中提取出位置 $k$ 的格式为:
% $\alpha_i=\rho_i(s^i)^\top q^{i+1}$ ,
% $q^{i}=q^{i+1}-\alpha_i y^i$。其中 $i$ 从 $k-1$ 减小到 $k-m$。
for di = status:-1:1
k = perm(di);
alpha(di) = (q'*SK(:,k)) * rho(k);
q = q - alpha(di)*YK(:,k);
end
%%%
% $r^{k-m}=\hat{H}^{k-m}q^{k-m}.$
y = q/(rho(pos)* (ygk'*ygk));
%%%
% 第二个循环,迭代格式 $\beta_{i}=\rho_i(y^i)^\top r^i$,
% $r^{i+1}=r^i+(\alpha_i-\beta_i)s^i$。代码中的 |y| 对应于迭代格式中的 $r$,当两次循环结束时,以返回的 |y| 的值作为下降方向。
for di = 1:status
k = perm(di);
beta = rho(k)* (y'* YK(:,k));
y = y + SK(:,k)*(alpha(di)-beta);
end
end
end
非凸非光滑函数的BFGS算法
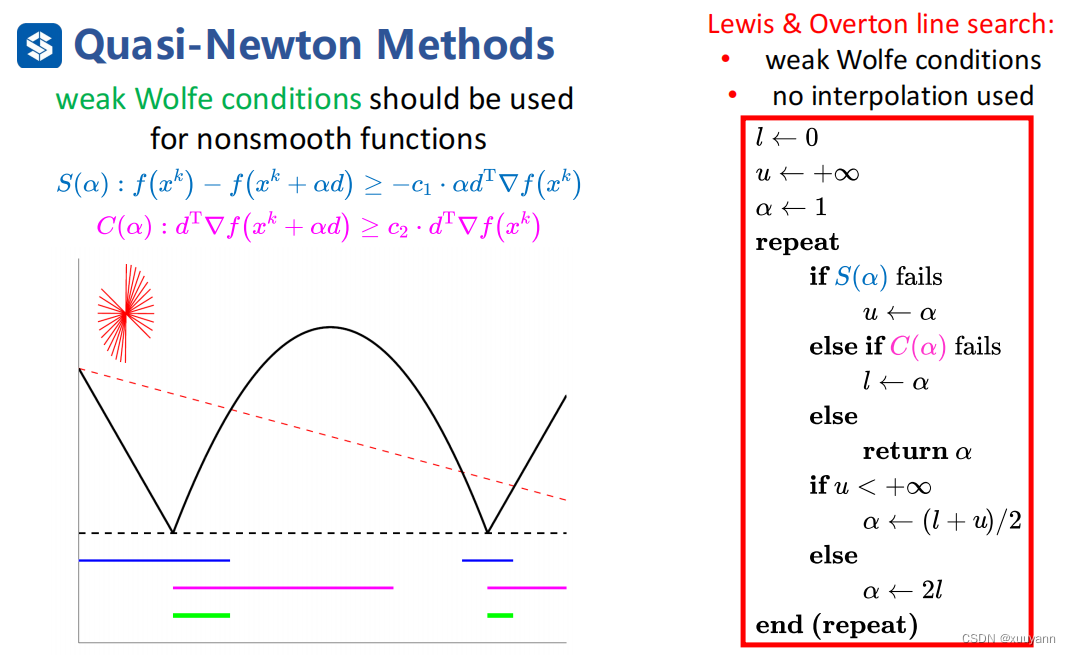
那么更一般化,对于非凸且非光滑函数而言,L-BFGS能适用吗?答案是可以,但线搜索策略只能使用weak Wolfe条件,不能使用strong Wolfe条件,另外在weak Wolfe条件基础上使用Lewis-Overton line search(一个高效率且鲁棒性强的线搜索策略)。
如下图所示,若函数是光滑的,满足strong Wolfe中第一个条件的是左图中蓝色线对应的函数部分,满足第二个条件的是粉色线对应部分,故同时满足strong Wolfe条件的是两者重叠的绿线对应部分。但是对于非凸且非光滑函数而言,找不到满足strong Wolfe第二个条件对应的函数部分,约束太强以至于存在失败可能,weak Wolfe条件则不会出现这个问题。因此,对于非光滑函数而言,在线搜索策略中采用weak Wolfe条件,同时为了避免函数拟合,在weak Wolfe条件基础上使用Lewis-Overton line search。
综上所述,对于非凸非光滑函数而言,weak Wolfe+Lewis-Overton line search+基于Cautious update的L-BFGS算法可以解决该类型的优化问题,算法流程如下所示:


参考文献
机器人中的数值优化
最优化:建模、算法与理论/最优化计算方法
牛顿法与拟牛顿法学习笔记(一)牛顿法
逻辑回归模型及LBFGS的Sherman Morrison(SM) 公式推导
Lewis, A.S., Overton, M.L. Nonsmooth optimization via quasi-Newton methods. Math. Program. 141, 135–163 (2013). https://doi.org/10.1007/s10107-012-0514-2
Li D H, Fukushima M. On the global convergence of the BFGS method for nonconvex unconstrained optimization problems[J]. SIAM Journal on Optimization, 2001, 11(4): 1054-1064.