在经过了2021年元宇宙概念落地和普及后，2022年成为元宇宙相关产业井喷式发展的一年。元宇宙产业委在2022年多项成果荣登行业影响力榜单。

     2021-2022元宇宙科技传播图书影响力榜发布，元宇宙产业委好书上榜

      2022年9月，两办印发《关于新时代进一步加强科学技术普及工作的意见》，为了响应文件中提出的“构建政府、社会、市场等协同推进的社会化科普发展格局”“推进科普智库建设”“实施国际科学传播行动”号召，12月30日，中国科技新闻学会元宇宙科技传播专委会和中国互联网新闻中心(中国网)联合主办“2022元宇宙科技传播论坛”暨“元宇宙科技传播智库”成立仪式。

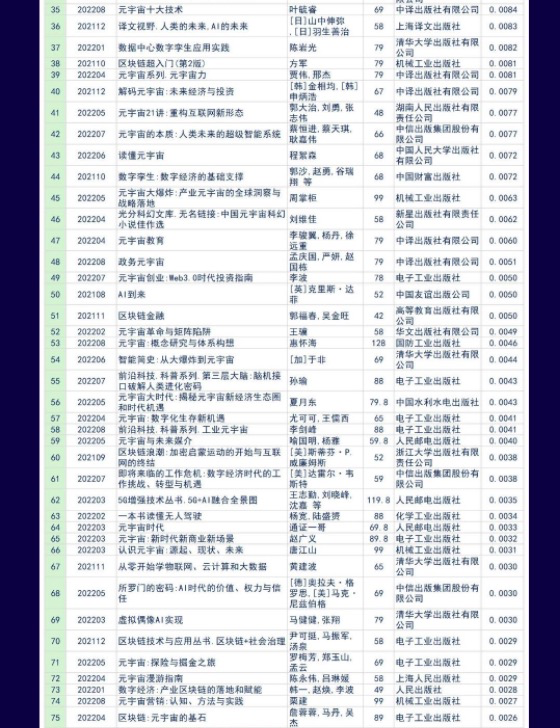
论坛现场主办方发布了《2022中国元宇宙科技传播白皮书》，并联合北京开卷发布了“2021-2022元宇宙科技传播图书影响力榜”。其中，元宇宙产业委策划出版的图书《元宇宙》、《元宇宙十大技术》荣登《2021-2022元宇宙科技传播图书影响力榜》榜单。

《元宇宙》 

《元宇宙十大技术》

在此次论坛上，由CICG元宇宙国际传播实验室负责人、元宇宙产业委常务委员赵萱主持，清华大学新闻与传播学院副院长张铮、元宇宙系列畅销书作者邢杰、元宇宙产业委联席秘书长叶毓睿、北京国家数字出版基地研究院首席研究员、元宇宙产业委副主任委员苏彤等专家学者还围绕“挖掘新动力，构建新文明”的主题进行了对话。

论坛上，专家学者们围绕“挖掘新动力，构建新文明”的主题进行了对话

中国科技新闻学会元宇宙科技传播专委会总协调人、奥运品牌专家杨曦沦提出两大倡议：一是将每年的12月30日设定为“中国元宇宙品牌日”，集中展现元宇宙的年度创见与创新成果；二是从明年开始汇聚各方力量，将元宇宙科技传播论坛打造为元宇宙领域的奥运会——“元奥会”，通过链接全球科技与智慧，创造人类新繁荣。

行而不辍，未来可期。与会代表相信，2023年必将成为“元宇宙实践之年”。

2022中国元宇宙大事件100在京发布 元宇宙产业委三大事件上榜

在由中国科技新闻学会元宇宙科技传播专委会与中国网等机构联合主办的2022元宇宙科技传播论坛上，作为元宇宙科技传播智库的共同发起方，《中国科技信息》杂志社与北京信息产业协会元宇宙专家委员会联合发布了《2022中国元宇宙大事件100》。

《中国科技信息》杂志社社长杨曦沦代表“2022中国元宇宙大事件100”编委会对榜单进行了解读。杨曦沦介绍说，如果2021被称之为元宇宙元年，2022就是中国元宇宙“千帆竞发，百舸争流”的一年。“2022中国元宇宙大事件100”榜单作为元宇宙科技传播智库推出的一项重要成果，旨在通过观察梳理2022中国元宇宙领域内不同相关方的行为及结果，帮助业界在新经济环境中对中国元宇宙的生态及发展有一个多维度的认知，为2023年优化中国元宇宙发展生态提供一个动态观察与研判体系。

千帆竞发 百舸争流

2022年中国元宇宙大事件100 

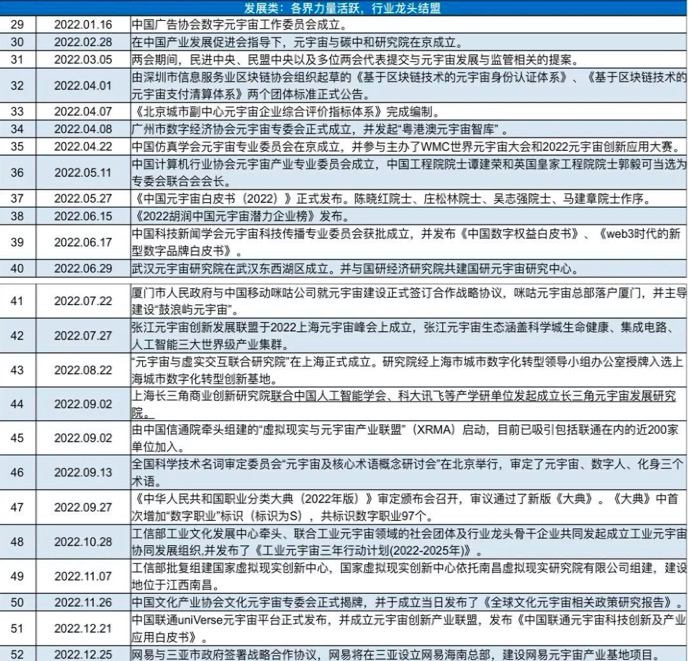
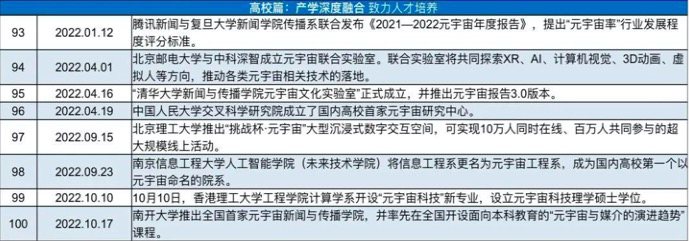
在这100大元宇宙事件当中，元宇宙产业委主办的元宇宙共识大会、钱学森诞辰111周年系列纪念活动、全球元宇宙大会赫然在列。

元宇宙共识大会

 钱学森诞辰111周年系列纪念活动

全球元宇宙大会

回顾2022，随着元宇宙概念的继续火热，元宇宙相关产业培育在全国范围内呈现良好的发展势头，VR、AR、区块链、AI等众多技术不断成熟，元宇宙与零售、文娱、旅游、社交、健身、教育、医疗、办公、军事等领域“梦幻联动”，走入我们生活的方方面面。可以预计，2023年将成为信息技术与数字经济为新经济的增长引擎的“元宇宙实践之年”，元宇宙场景应用将成为元宇宙科技关注的重点领域。