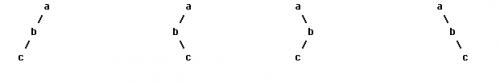题目描述
我们都很熟悉二叉树的前序、中序、后序遍历,在数据结构中常提出这样的问题:已知一棵二叉树的前序和中序遍历,求它的后序遍历,相应的,已知一棵二叉树的后序遍历和中序遍历序列你也能求出它的前序遍历。然而给定一棵二叉树的前序和后序遍历,你却不能确定其中序遍历序列,考虑如下图中的几棵二叉树:
所有这些二叉树都有着相同的前序遍历和后序遍历,但中序遍历却不相同。
输入格式
输A数据共两行,第一行表示该二叉树的前序遍历结果s1,第二行表示该二叉树的后序遍历结果s2。
输出格式
输出可能的中序遍历序列的总数,结果不超过长整型数。
输入输出样例
输入 #1复制
abc cba输出 #1复制
4说明/提示
无提示
1.我们可以了解到当一个节点只有单个的左孩子和右孩子的时候,前序遍历和后序遍历是一样的。
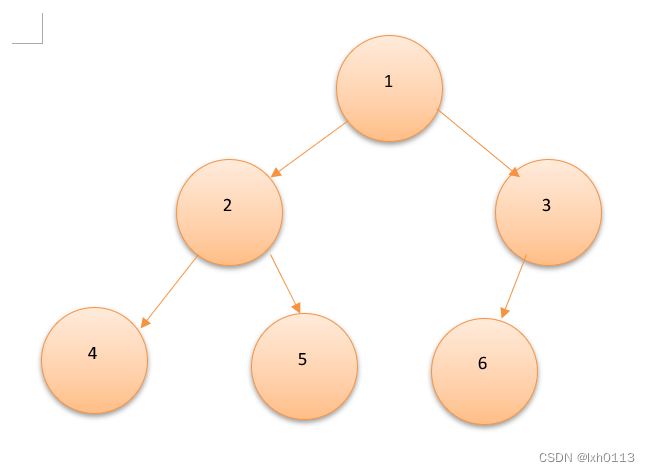
因为只有单个节点的话先序和后序是分不清中序的,因为先序遍历是 根左右,而后序是左右根,当只有单个节点就会变成 :
先序是:根左(或者右)1->2->4->5->3->6
后序是:左(或者右)根 4->5->2->6->3->1
如果有其他的节点,因为先序和后序左右子树是恰恰相反的,是可以确定的,所以只有当只有单个节点的时候,才会右多种可能性。下面打一个比方:
(1)在这里,我们可以先确定根,继而是左子树我们看的第一个出现在先序的不是左子树就会使右子树的根,如果是右子树的根那么出现在导数第二个的应该是2,而不是3,所以2会是左子树,那么我们可以知道3肯定是右子树。
(2)我们已经确立2是左子树,2是根,那么接下来在先序遍历顺序中,我们可以知道4和5是属于左子树的,因为到了3,3已经是右子树的根,先序遍历的特点是根左右,所以4 5 是它的下属节点,而我们结合后序遍历看,先是 4 再是 5 ,因为后序遍历是 左右根,所以4 5 是 2 的左右孩子,而不是4 和 5 当中还能有下属节点,如果 5 是 4 的节点那么先序就不会是 4->5 ,4 是 5的节点就更不可能了。
(3)我们已经确定了左子树,我们继而看右子树。我们知道 3 是右子树根节点。还剩下 6 这一个数字了,我们是无法确定 6 这个节点是左孩子还是右孩子的。所以他会有俩个可能性。
那么如何变成代码?
我们遍历先序数组str1,和遍历后序数组str2

如果str1[i]==str2[j],就说明找到了一个节点相等,str1[i+1]==str2[j-1],这个是说明满足当前相等的节点只有一个节点的情况。因为先序遍历是 根左(右)而后序遍历是左(右)根,所以记录下来有几个这样的节点。
最后输出1<<c即可,为什么不使用pow,因为pow返回值是double,并不是很适合。你也可以在记录的同时,去*2是可以的。
C语言代码如下:
#include<stdio.h>
#include<string.h>
int main()
{
char str1[300],str2[300];
int i,j;
long long s=1,c=0;
scanf("%s%s",str1,str2);
for(i=0;i<strlen(str1);i++)
{
for(j=1;j<strlen(str2);j++)
{
if(str1[i]==str2[j]&&str1[i+1]==str2[j-1])
c++;
}
}
printf("%lld\n",s<<c);
}C++代码如下:
#include <iostream>
#include <bits/stdc++.h>
#include <cstring>
using namespace std;
int main()
{
char str1[300], str2[300];
int i, j;
long long s = 1;
cin >> str1 >> str2;
for (i = 0; i < strlen(str1)-1; i++)
{
for (j = 1; j < strlen(str2); j++)
{
if (str1[i] == str2[j] && str1[i + 1] == str2[j - 1])
s*=2;
}
}
cout << s << endl;
return 0;
}