之前调试kenel ，如果kenenl崩溃会，通过内核system.map定位log_buf变量地址，给cpu复位，在u-boot中读取对应的物理地址，即可知道最终内核崩溃最后打出的消息。

我在使用 5.4.154这个内核版本，中没有log_buf这个变量，经过分析 kernel/printk.c文件，我尝试打出这个日志文件，printk.c中部分源码如下：

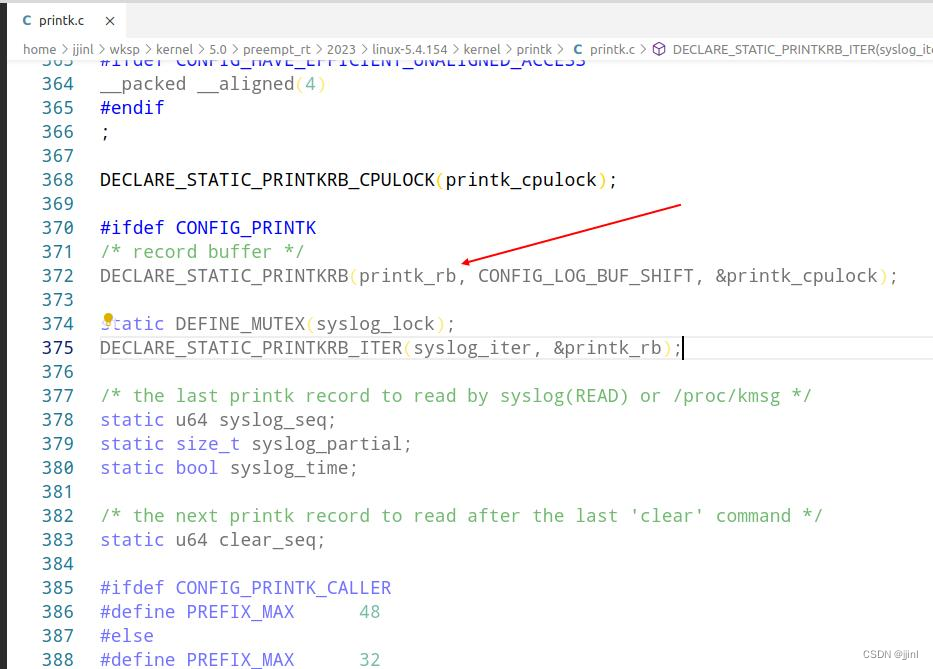
 其中在372行定义

DECLARE_STATIC_PRINTKRB(printk_rb, CONFIG_LOG_BUF_SHIFT, &printk_cpulock);

我查了这个宏定义在 include/linux/printk_ringbuffer.h这个头文件中，这个宏定义如下

#define DECLARE_STATIC_PRINTKRB(name, szbits, cpulockptr)		\
static char _##name##_buffer[1 << (szbits)]				\
	__aligned(__alignof__(long));					\
static DECLARE_WAIT_QUEUE_HEAD(_##name##_wait);				\
static void _##name##_wake_work_func(struct irq_work *irq_work)		\
{									\
	wake_up_interruptible_all(&_##name##_wait);			\
}									\
static struct irq_work _##name##_wake_work = {				\
	.func = _##name##_wake_work_func,				\
	.flags = IRQ_WORK_LAZY,						\
};									\
static struct printk_ringbuffer name = {				\
	.buffer = &_##name##_buffer[0],					\
	.size_bits = szbits,						\
	.seq = 0,							\
	.lost = ATOMIC_LONG_INIT(0),					\
	.tail = ATOMIC_LONG_INIT(-111 * sizeof(long)),			\
	.head = ATOMIC_LONG_INIT(-111 * sizeof(long)),			\
	.reserve = ATOMIC_LONG_INIT(-111 * sizeof(long)),		\
	.cpulock = cpulockptr,						\
	.ctx = ATOMIC_INIT(0),						\
	.wq = &_##name##_wait,						\
	.wq_counter = ATOMIC_LONG_INIT(0),				\
	.wq_work = &_##name##_wake_work,				\
}

把这行代码进行宏展开

DECLARE_STATIC_PRINTKRB(printk_rb, CONFIG_LOG_BUF_SHIFT, &printk_cpulock);

等价与

#define DECLARE_STATIC_PRINTKRB( szbits, cpulockptr)
//只替换name

static char _printk_rb_buffer[1 << (szbits)] __aligned(__alignof__(long));
static DECLARE_WAIT_QUEUE_HEAD(_printk_rb_wait);

static void _printk_rb_wake_work_func(struct irq_work *irq_work)
{
	wake_up_interruptible_all(&_printk_rb_wait);
}

static struct irq_work _printk_rb_wake_work = {
	.func = _printk_rb_wake_work_func,
	.flags = IRQ_WORK_LAZY,	
};	

static struct printk_ringbuffer printk_rb = {
	.buffer = &_printk_rb_buffer[0],
	.size_bits = szbits,				
	.seq = 0,					
	.lost = ATOMIC_LONG_INIT(0),		
	.tail = ATOMIC_LONG_INIT(-111 * sizeof(long)),
	.head = ATOMIC_LONG_INIT(-111 * sizeof(long)),
	.reserve = ATOMIC_LONG_INIT(-111 * sizeof(long)),
	.cpulock = cpulockptr,				
	.ctx = ATOMIC_INIT(0),					
	.wq = &_printk_rb_wait,					
	.wq_counter = ATOMIC_LONG_INIT(0),		
	.wq_work = &_printk_rb_wake_work,		
}

可以看到上面宏定义 _printk_rb_buffer的数组，做缓冲区，我们只需要读取这个数据就可以，

在system.map中搜索_printk_rb_buffer中搜索如下图：

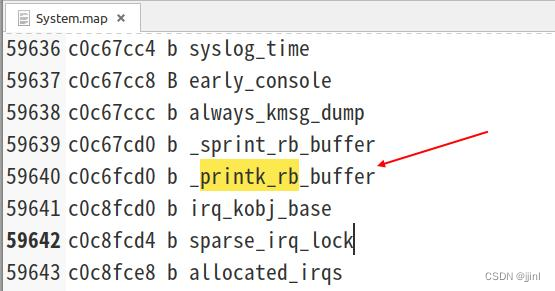
 由于ZYNQ的DDR是从0x0开始，根据system.map中的值0xc0c6fcd0,减去0xc0000000，在u-boot中通过md读取0x00c6fcd0就可以。

我使用的是ZYNQ平台，通过vivado的sdk工具，读取

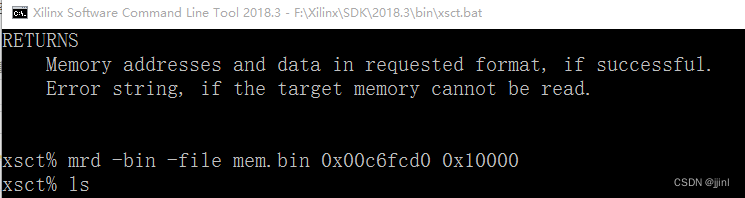
 通过二进制工具打开，效果如下图

 

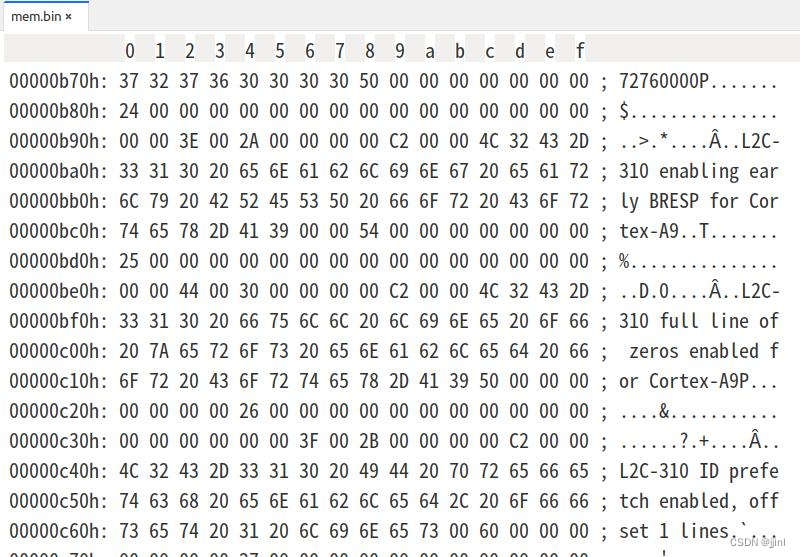
这个缓冲区数据有格式，没有仔细研究，将就能看。

本文章做个笔记，下次调试再翻看。