集合与容器：List、HashMap（II）

news2025/4/5 8:10:09

一、ArrayList

是集合框架中最核心的动态数组实现，高频使用的容器之一。

1. 核心数据结构

基于数组实现，维护elementData数组存储元素：

transient修饰的elementData不会被默认序列化（通过自定义序列化逻辑优化存储）

2. 动态扩容机制

当添加元素时发现容量不足，触发 grow(int minCapacity) 扩容：

核心逻辑：

① 扩容倍率：新容量 = 旧容量 * 1.5 （位运算 oldCapacity >> 1 代替除法优化性能）
② 数组拷贝：Arrays.copyOf() 底层使用System.arraycopy()，为本地方法（效率高）

3. 添加元素流程

以add(E e)为例：

容量检查：若当前数组已满，触发扩容后再插入
尾部插入：时间复杂度O(1)

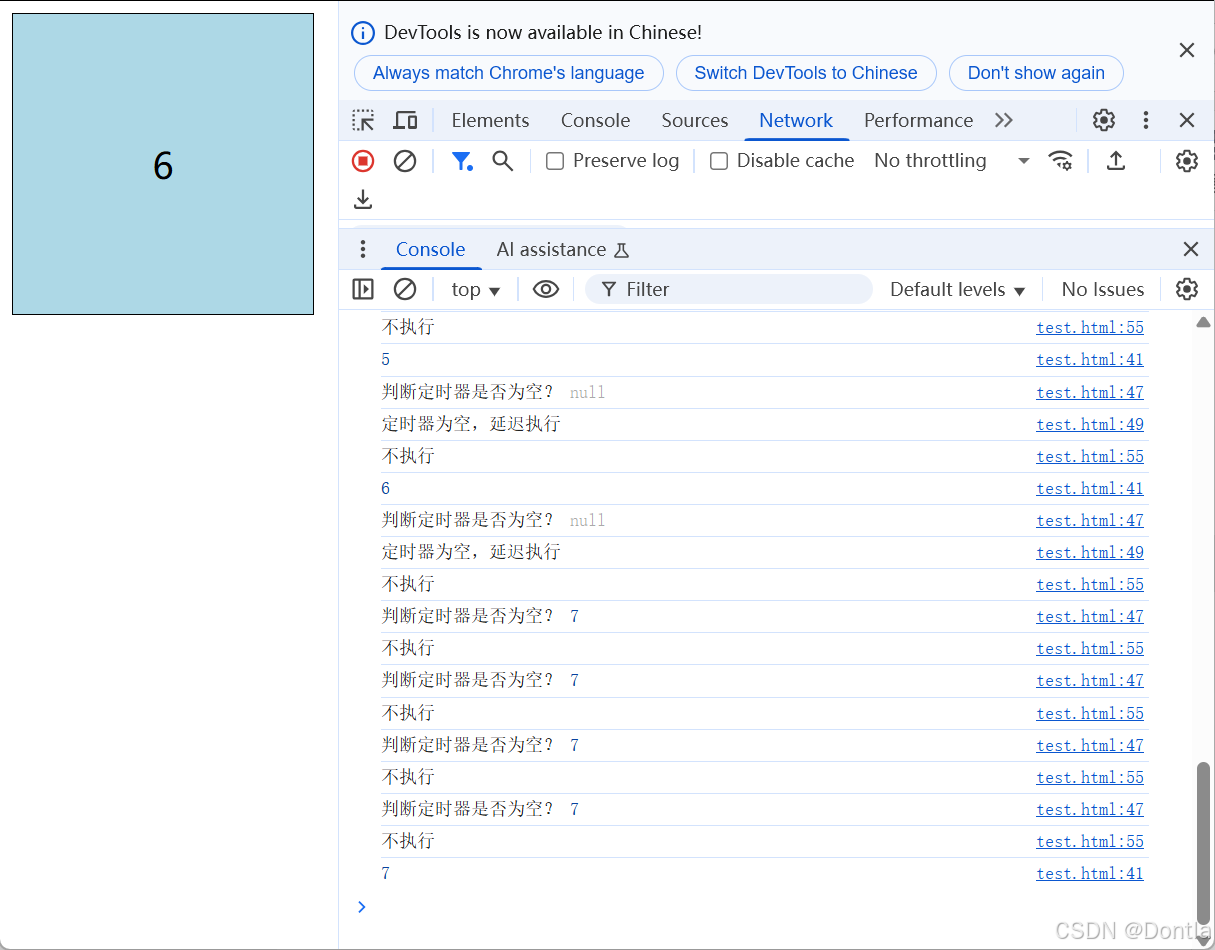
arrayList.add(a)：

场景1：第一次添加元素（空数组扩容）

触发条件：默认构造的ArrayList首次调用add()。（初始elementData为空数组）

流程：

minCapacity = size + 1 = 1
判断当前容量 elementData.length = 0，需要扩容
计算新容量 newCapacity = max(10, 1) = 10
新数组elementData = new Object[10]，将元素插入首位。

场景2：末尾插入且容量充足

ensureCapacityInternal(size + 1) --> 无需扩容
elementData[size++] = e --> 直接插入末尾，无需移动元素，O(1)时间复杂度

场景3：触发扩容（容量不足）

例：数组已满（size == elementData.length）时添加新元素。

扩容步骤：

oldCapacity = 10；
计算增长量 oldCapacity >> 1 = 5 --> newCapacity = 15；
Arrays.copyOf(elementData, 15) --> 快速本地方法拷贝数组；
扩容代价：数组拷贝O(n)，需要在插入时尽量避免频繁扩容；

安全检查方法：hugeCapacity(minCapacity)

hugeCapacity的决策逻辑分为：

case1：minCapacity 正常（非负且 <=MAX_ARRAY_SIZE）

返回 MAX_ARRAY_SIZE （即Integer.MAX_VALUE - 8）。

case2：minCapacity > MAX_ARRAY_SIZE

直接返回Integer.MAX_VALUE（允许尝试分配更大的容量，但可能导致OOM）。

异常处理：minCapacity < 0（溢出导致）

抛出OutOfMemoryError （申请容量已超过Integer.MAX_VALUE，无法满足）

场景4：中间插入（需移动元素-add(int index, E e)）

例如：list.add(2, "hello"); // 在索引2处插入元素

流程：

检查索引合法性（index >= 0 && index <= size）
检查容量 --> 不够则扩容
计算需要移动的元素数量：numMoved = size - index = 3.
调用System.arraycopy(elementData, 2, elememtData, 3, numMoved)，将原数据从索引2开始的元素后移1位。
elementData[2] = "hello".
时间复杂度：平均O(n)

核心方法：

4. 删除元素流程

核心点：

移动代价：平均时间复杂度O(n)，末尾删除为O(1)
GC处理：手动赋值null避免内存泄漏

5. modCount作用

迭代器通过modCount追踪结构性修改：

结构性修改：

任何导致size变化或元素位置变化的操作（增、删、排序等）
多线程问题：未同步时快速失败机制能检测部分并发问题

6. 线程安全性

非线程安全：ArrayList的设计不保证多线程环境下的安全

替代方案：

Collections.synchronizedList(new ArrayList<>()) 同步包装类
CopyOnWriteArrayList写时复制容器（适合读多写少场景）

7. 性能优化技巧

（1）初始化时指定容量

ArrayList<String> list = new ArrayList<>(1000);  // 直接指定初始容量

（2）批量操作优先：避免循环内多次扩容

list.addAll(Arrays.asList("A","B","C"));   // 批量添加减少扩容次数

（3）谨慎使用contains/remove(Object)：时间复杂度O(n)，高频操作可改用HashSet

二、LinkedList

是一个基于双向链表实现的集合类，经常被拿来和ArrayList做比较。

LinkedList仅仅在头尾插入或者删除元素的时候时间复杂度近似O(1)，其他情况增删元素的平均时间复杂度都是O(n)。

LinkedList 中的元素是通过Node定义的：

1. 初始化

LinkedList中有一个无参构造函数和一个有参构造函数。

2. 获取元素

LinkedList获取元素相关的方法有三个：

（1）getFirst()

（2）getLast()

（3）get(int index)

核心在于node(int index)方法：

get(int index) 和 remove(int index) 等方法内部都调用了该方法来获取对应的节点。

该方法通过比较索引值与链表size的一半大小来确定从链表头还是尾开始遍历。如果索引值小于size的一半，就从链表头开始遍历，反之从链表尾开始遍历。这样可以在较短的时间内找到目标节点，充分利用了双向链表的特性来提高效率。

3. 插入元素

add() 方法有两个版本：

add(E e)：用于在LinkedList的尾部插入元素，即将新元素作为链表的最后一个元素，时间复杂度为O(1)。
add(int index, E element)：用于在指定位置插入元素，这种插入方式需要先移动到指定位置，再修改指定节点的指针完成插入/删除，因此需要移动平均n/4个元素，时间复杂度为O(n)。