1 前言

在数据结构中学过哈希概念以及哈希在内存中的应用，在实际的应用问题中哈希技术也应用十分广泛如在推荐系统以及图神经网络技术中，所以在此总结一下哈希的相关概念以及minHash以及其实际应用，其中多有参考别的文献内容，相关参考一并列在参考文献中。

2 哈希函数的定义

Hash（哈希），又称“散列”。散列（hash）英文原意是“混杂”、“拼凑”、“重新表述”的意思。在某种程度上，散列是与排序相反的一种操作，排序是将集合中的元素按照某种方式比如字典顺序排列在一起，而散列通过计算哈希值，打破元素之间原有的关系，使集合中的元素按照散列函数的分类进行排列。也可以说：Hash函数是一个把大范围的数据映射到小范围的函数。比方说，商店里有三件商品，价格分别为 $99 、 199$ 和 $299$ 。我们是否需要开一个 $300$ 维的数组 $H$ 来存储这三件商品，使得 $H (99) = 0 商品$ ， $H (199) = 1 商品$ ， $H (299) = 2 商品$ 。答案是否定的，由于十位和个位都是 $9$ ，因此我们可以只关注百位 $(0, 1, 2)$ 。于是我们只需要一个三维的数组 $B$ 使得 $B (0) = 0 商品$ ， $B (1) = 1 商品$ ， $B (2) = 2 商品$ 。在这个例子中，将三位数 $x yz$ 映射为 $x$ 就是一个哈希函数。
下面再举一个内存中应用哈希的例子，内存中通常使用数组或者链表来存储元素，一旦存储的内容数量特别多，需要占用很大的空间，而且在查找某个元素是否存在的过程中，数组和链表都需要挨个循环比较，而通过哈希计算，可以大大减少比较次数。
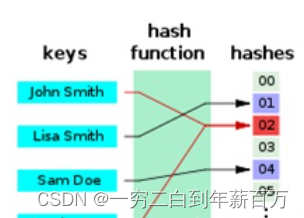
在这里插入图片描述

举个栗子：
现在有 4 个数 {2,5,9,13}，需要查找 13 是否存在。
1.使用数组存储，需要新建个数组 new int[]{2,5,9,13}，然后需要写个循环遍历查找：
这样需要遍历 4 次才能找到，时间复杂度为 O(n)。（当然也可以优化用二分查找等吗，但是复杂度仍然大于O(1)）

 int[] numbers = new int[]{2,5,9,13};
    for (int i = 0; i < numbers.length; i++) {
        if (numbers[i] == 13){
            System.out.println("find it!");
            return;
        }
    }

2.而假如存储时先使用哈希函数进行计算，这里我随便用个函数：

H[key] = key % 3;
四个数 {2,5,9,13} 对应的哈希值为：

 H[2] = 2 % 3 = 2;
 H[5] = 5 % 3 = 2;
 H[9] = 9 % 3 = 0;
 H[13] = 13 % 3 = 1;

然后把它们存储到对应的位置。
当要查找 13 时，只要先使用哈希函数计算它的位置，然后去那个位置查看是否存在就好了，本例中只需查找一次，时间复杂度为 O(1)。

常见的哈希函数构造方法可以见参考文献【2】。除此之外，从举的例子可以看出，选用哈希函数计算哈希值时，可能不同的 key 会得到相同的结果，一个地址怎么存放多个数据呢？这就是冲突。常用的主要有解决冲突的方法也可见参考文献【2】。

3 miniHash函数

miniHash原理：MinHash是基于Jaccard Index相似度（海量数据不可行）的算法,一种降维的方法。
minHash的基本原理:在A∪B这个大的随机域里，选中的元素落在A∩B这个区域的概率，这个概率就等于Jaccard的相似度。

问题引入：在数据挖掘中，一个最基本的问题就是比较两个集合的相似度。通常通过遍历这两个集合中的所有元素，统计这两个集合中相同元素的个数，来表示集合的相似度；这一步也可以看成特征向量间相似度的计算（欧氏距离，余弦相似度）。当这两个集合里的元素数量异常大（特征空间维数很大），同时又有很多个集合需要判断两两间的相似度时，传统方法会变得十分耗时，最小哈希（minHash）可以用来解决该问题。

这里需要注意一个问题：minHash与传统的hash的区别？在文本相似性度量的问题下，我们来看待这个问题，在文本度量的情况下hash就是将不同长度规则的文本转化成相同长度的字符串，用这些相同长度的字符串来表示原文本。但是传统hash存在一个问题是，相同内容的文本会生成相同的hash，但是相似的文本（可能就是一个字的差别）生成的hash会有很大的不同。但是我们在做文本相似度时，希望对相似的文本生成相似的hash，这样我们只需要计算一个个特定长度的hash值之间相似度，就可以近似得到原文本之间的相似度了，显然传统的hash算法是做不到这一点的。

4 miniHash的例子

假设现在有4个集合，分别为 $S_1, S_2, S_3, S_4$ ；其中， $S_1=\{a,d\}, S_2=\{c\}, S3=\{b,d,e\}, S_4=\{a,c,d\}$ ，所以全集 $U=\{a,b,c,d,e\}$ 。我们可以构造如下 $0 - 1$ 矩阵:
在这里插入图片描述
为了得到各集合的最小哈希值，首先对矩阵进行随机行打乱，则某集合（某一列）的最小哈希值就等于打乱后的这一列第一个值为1的行所在的行号。举一个例子：定义一个最小哈希函数 $h$ ，用于模拟对矩阵进行随机行打乱，打乱后的 $0 - 1$ 矩阵为:
在这里插入图片描述
如图所示， $h(S_1)=2, h(S_2)=4, h(S_3)=0, h(S_4)=2$
在经过随机行打乱后，两个集合的最小哈希值相等的概率等于这两个集合的Jaccard相似度，证明如下：

现仅考虑集合 $S_1$ 和 $S_2$ ，那么这两列所在的行有下面3种类型：
1、 $S_1$ 和 $S_2$ 的值都为 $1$ ，记为 $X$
2、只有一个值为 $1$ ，另一个值为 $0$ ，记为 $Y$
3、 $S 1$ 和 $S 2$ 的值都为 $0$ ，记为 $Z$

$S_1$ 和 $S_2$ 交集的元素个数为 $x$ ，并集的元素个数为 $x + y$ ，所以 $sim(S_1,S_2) = Jaccard(S_1,S_2) = x/(x+y)$ 。接下来计算 $h(S_1)=h(S_2)$ 的概率，经过随机行打乱后，从上往下扫描，在碰到 $Y$ 行之前碰到 $X$ 行的概率为 $x / (x + y)$ ，即 $h(S_1)=h(S_2)$ 的概率为 $x / (x + y)$ 。