目录

1.调用math库函数中的pow函数实现n的k次方

2.创造pow函数实现n的k次方

3.递归实现n的k次方（含图解）

1.调用math库函数中的pow函数实现n的k次方

        pow函数的功能：计算n的k次幂

        pow格式：pow(n,k)

#include <stdio.h>

#include <math.h>//头文件

int main()
{
	int n = 0;
	int k = 0;
	scanf("%d %d", &n, &k);

	int ret = pow(n, k);//运用pow函数

	printf("%d\n", ret);
	return 0;
}

2.创造pow函数实现n的k次方

注意要分三种情况，分别是：

                                        k = 0

                                        k < 0

                                        k > 0

        因为当k<0时，得到的是小数。所以注意要使用浮点数类型

float POW(int n,int k)
{
	float sum = n;
	if (k == 0)
	{
		return 1;
	}
	else if (k > 0)
	{
		for (int i = 1; i < k; i++)
		{
			sum *= n;
		}
		return sum;
	}
	else
	{
		k = -k;
		for (int i = 1; i < k; i++)
		{
			sum *= n;
		}
		return 1.0 / sum;
	}
	
}
int main()
{
	int n = 0;
	int k = 0;
	scanf("%d %d", &n, &k);

	float ret = POW(n, k);

	printf("%f \n", ret);
	return 0;
}

3.递归实现n的k次方（含图解）

        代码下方有图解

float POW(int n, int k)
{
	if (k == 0)
	{
		return 1;
	}
	else if (k > 0)
	{
		return n * POW(n, k - 1);
	}
	else//k<0的情况
	{
		return 1.0 / POW(n, -k);
	}
}
int main()
{
	int n = 0;
	int k = 0;
	scanf("%d %d", &n, &k);

	float ret = POW(n, k);

	printf("%f\n", ret);
	return 0;
}

        n = 2，k = 3的图解为：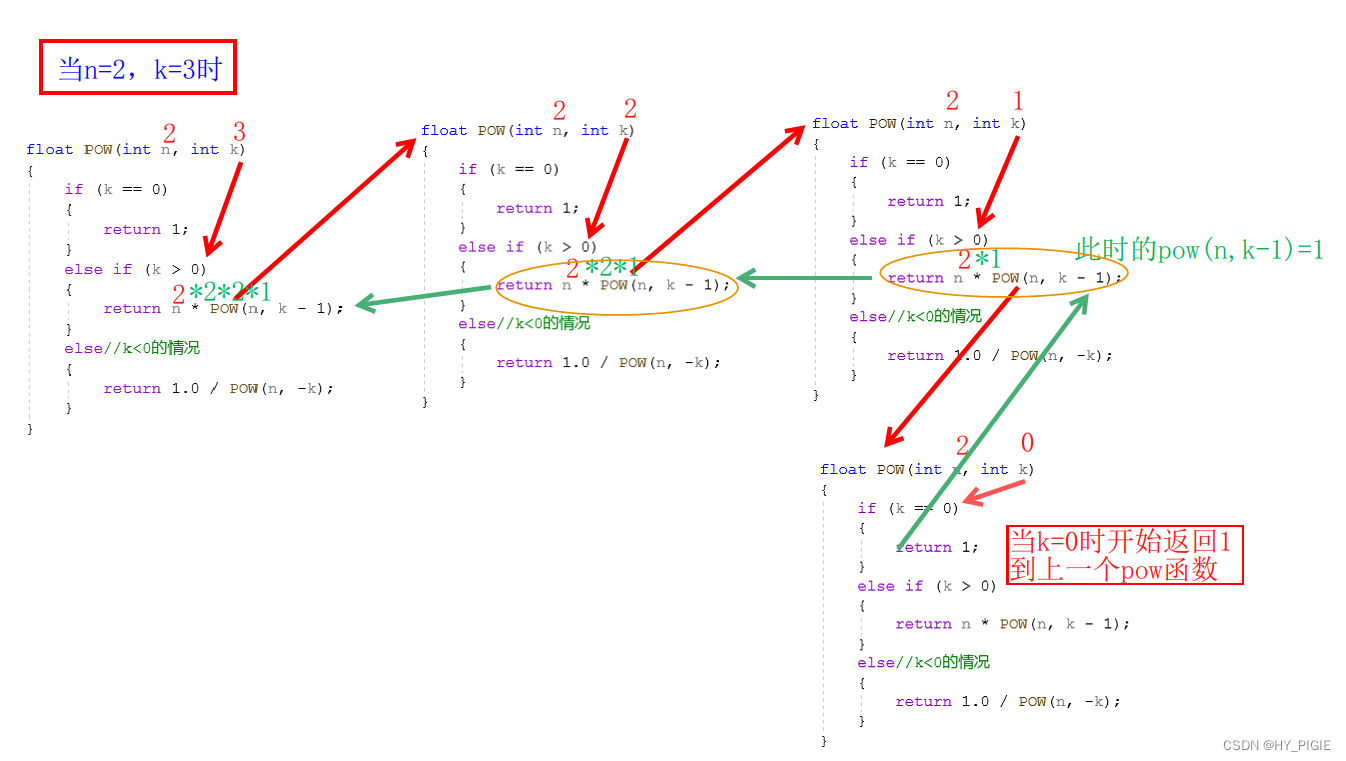

         当k<0时和k>0的递归方法大差不差，只是多了一步先将k转换成正数再放到pow函数中