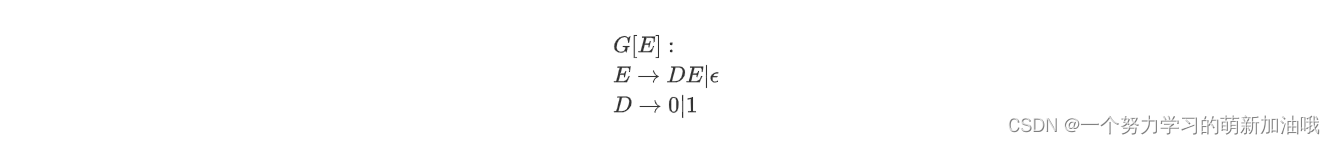【信息论与编码 沈连丰】第五章:离散信道及其信道编码
- 第五章 离散信道及其信道编码
- 5.1 信道的分类及其描述
- 5.2 无扰离散信道的传输特性
- 5.3 有扰离散信道的传输特性
- 5.4 译码准则
- 5.5 有扰离散信道的信道编码定理
- 5.6 信道编码定理的应用
第五章 离散信道及其信道编码
5.1 信道的分类及其描述
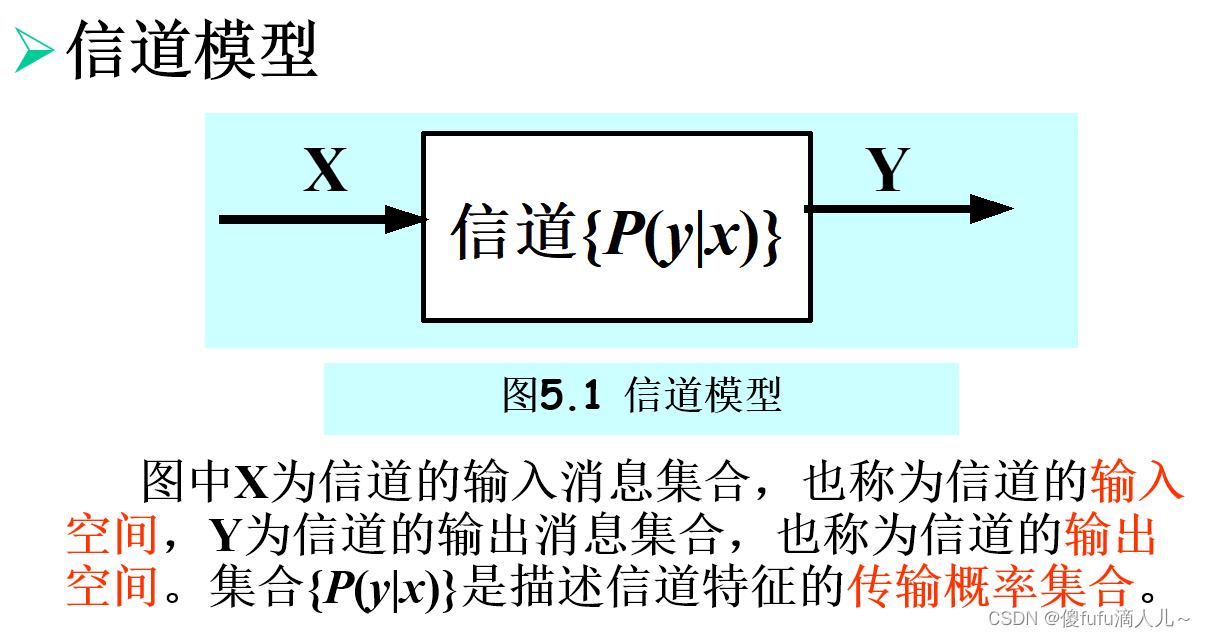
- 信道模型:
- 信道分类:



5.2 无扰离散信道的传输特性
- 信息传输速率:(注意区分信源编码器的信息传输速率和消息在信道中的信息传输速率)


- 信道容量:

- 均匀编码信道的信道容量:



5.3 有扰离散信道的传输特性
-
有扰离散信道的数学模型:
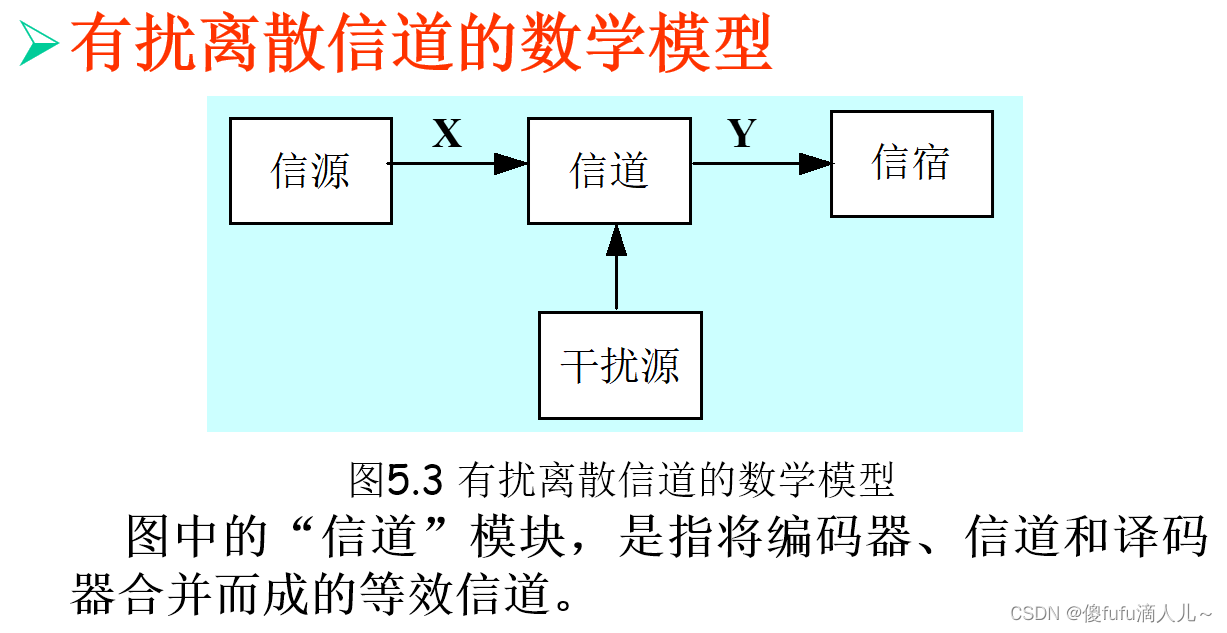
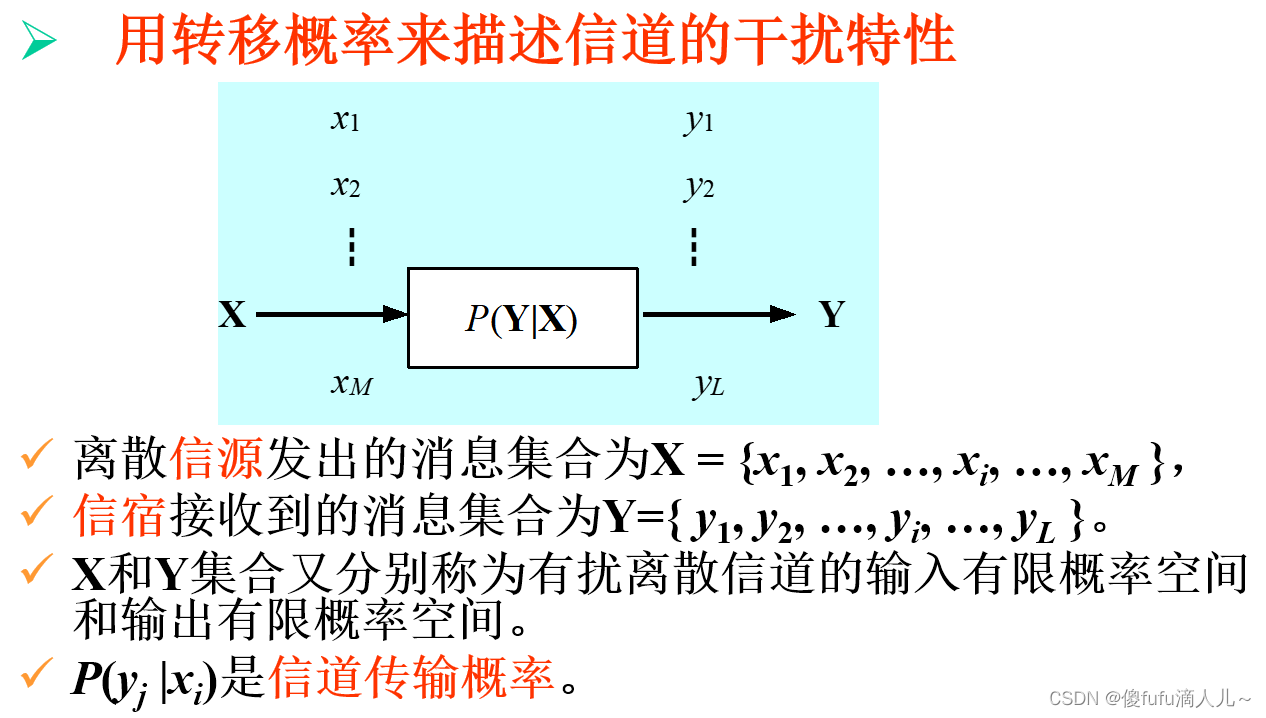
-
二进制对称信道:
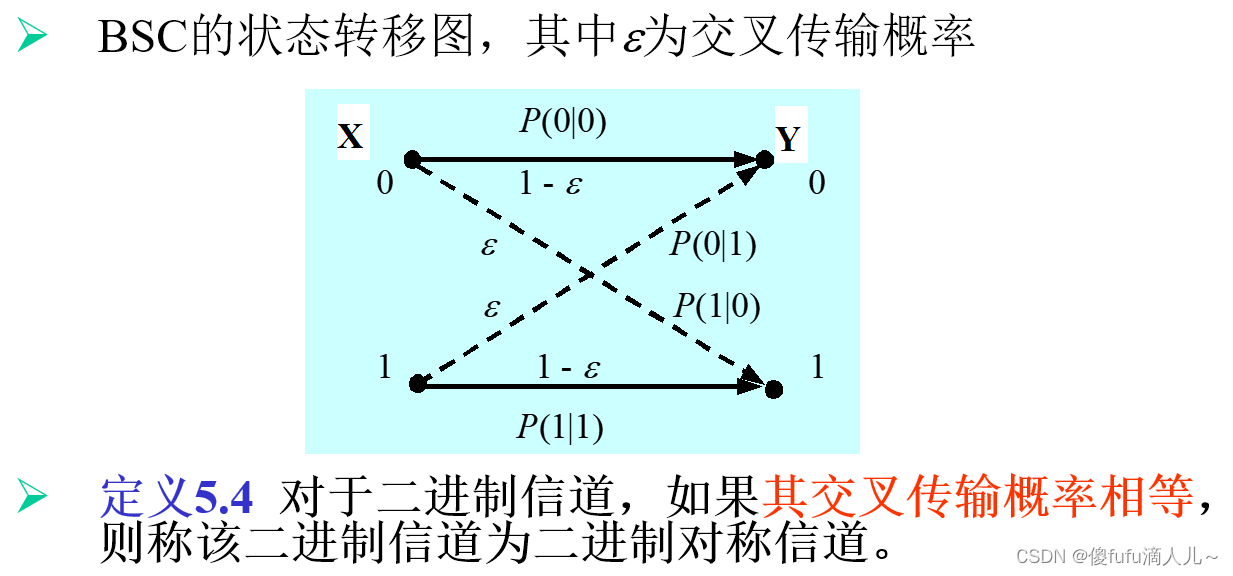

-
二进制删除信道:
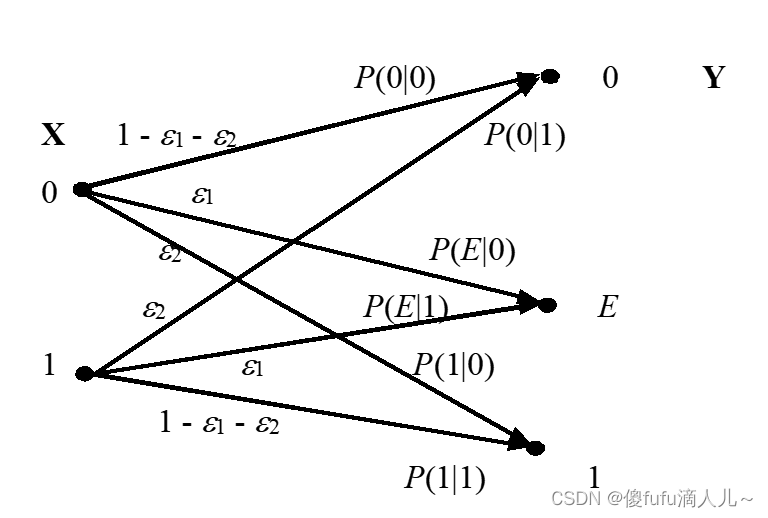

-
信息传输速率和平均互信息量的关系:


- 准对称信道:

- 准对称信道的信道容量:



- 串联信道:

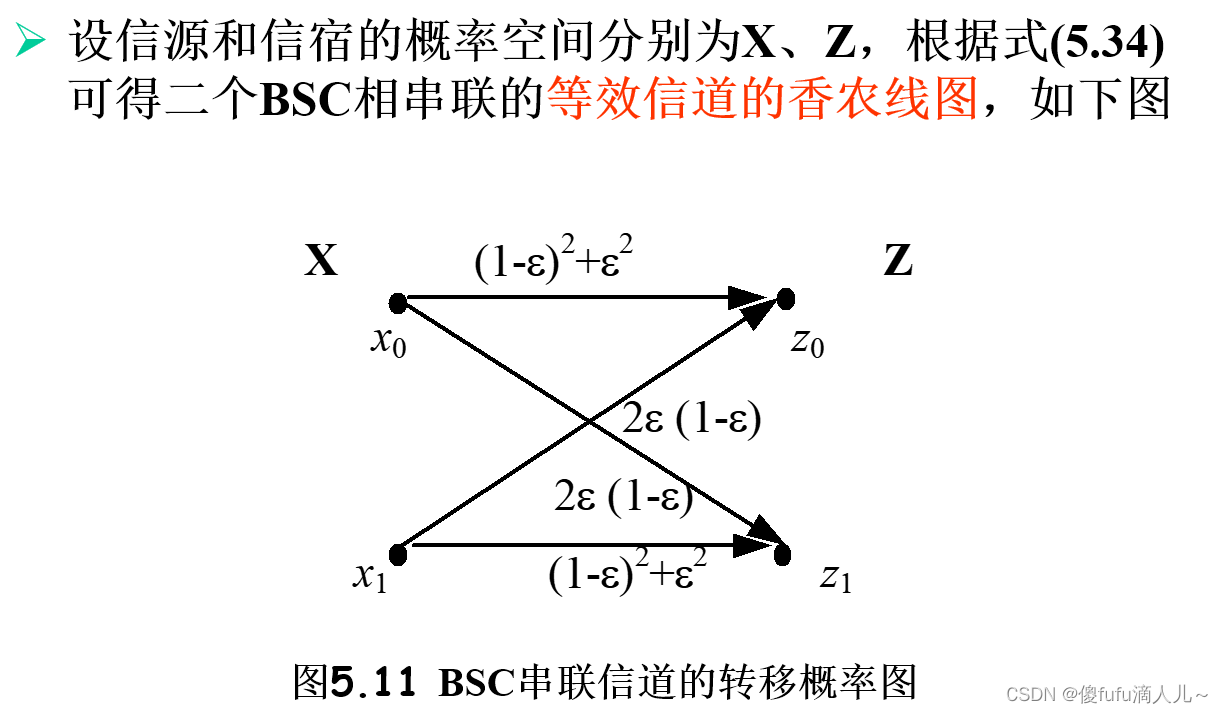


- 并联信道:
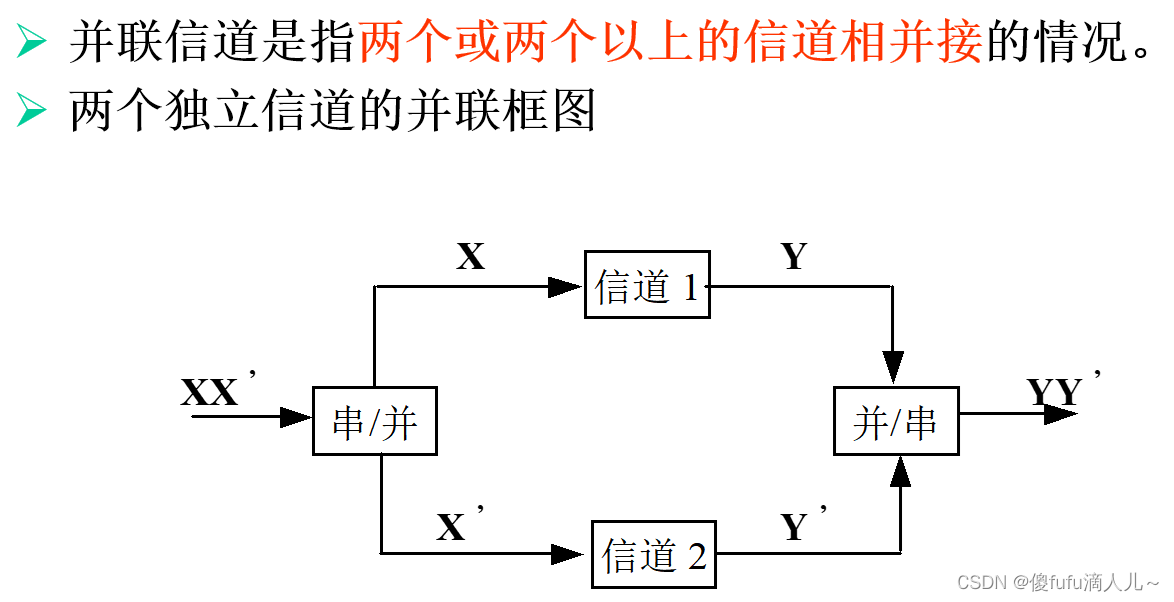


5.4 译码准则
- 译码准则:

- 最小错误概率准则:

例子:
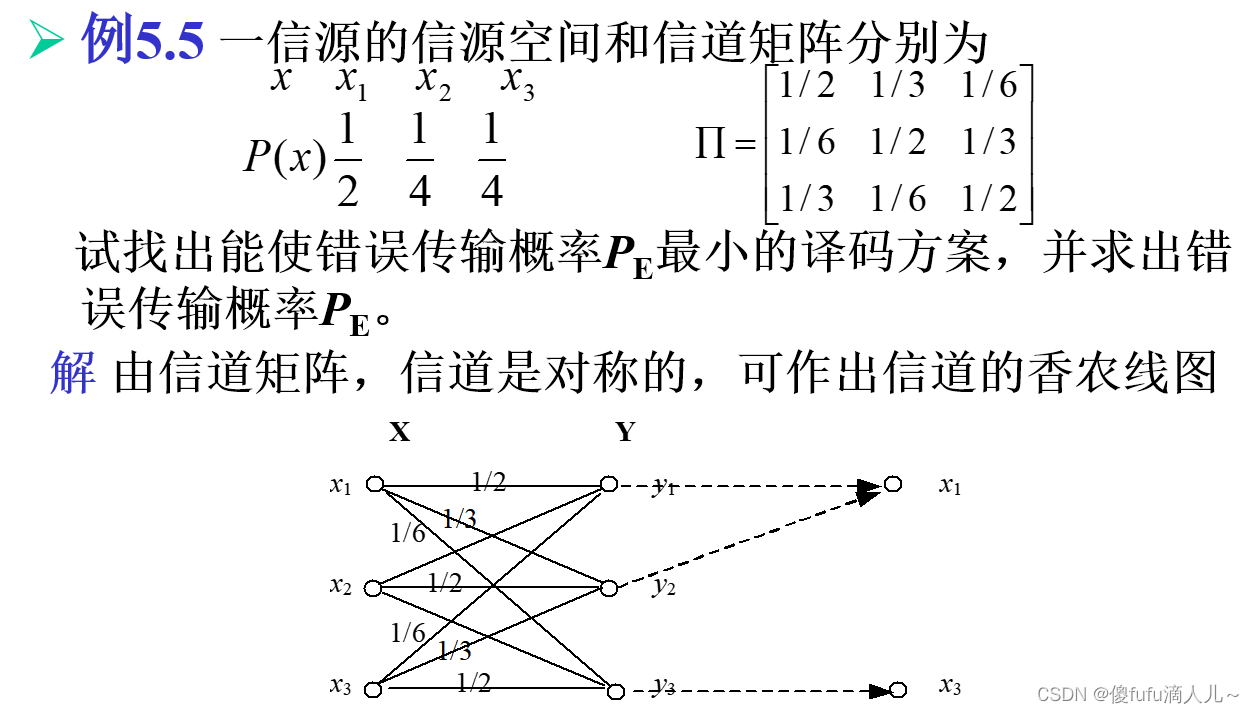


- 最大似然译码准则:


5.5 有扰离散信道的信道编码定理
- 汉明距离:


- 最大似然译码准则与汉明距离:

- 香农第二定理:


-
费诺不等式:

-
香农第二定理也是一个存在性定理,从理论上证明,平均错误译码概率趋近0、信道信息传输速率R无限趋近于信道容量的抗干扰信道编码是存在的。
5.6 信道编码定理的应用
- 减少误码率的措施: