视频教程：https://www.bilibili.com/video/BV12s411g7gU?p=155

向量

一个数字列表，表示各个维度上的有向位移；同时也是一个有大小有方向的物理量，大小及向量的模长，而方向即空间中向量的指向，可以表示物体的位置和方向

向量的形式

 

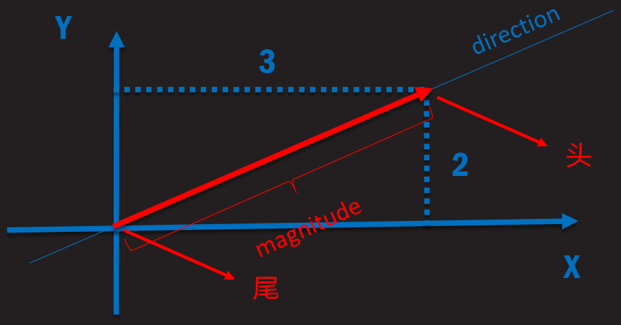
向量的大小(模)

向量各分量平方和的平方根 

  

API : 

Vector3.magnitude：模长

Vector3..sqrMagnitude：模长的平方

向量的方向 

 获取向量方向也称“标准化向量”，或“归一化向量”，即该向量的单位向量（大小为1的向量）。

几何意义︰将该向量拉长或者缩短，使模长等于1

  

API：

Vector3.normalized：获取该向量的单位向量

Vector3 vector2=vector1.normalized;//vector2为vector1的单位向量

Vector3.Normalize：将该向量自身设置为单位向量

vector1.Normalize();//将vector1自身设置为单位向量

private void Update()
{
    Demo01();
    Demo02();
}

//模长
private void Demo01()
{
    Vector3 pos = this.transform.position;

    float m01 = Mathf.Sqrt(Mathf.Pow(pos.x, 2) + Mathf.Pow(pos.y, 2) + Mathf.Pow(pos.z, 2));
    float m02 = pos.sqrMagnitude;
    float m03 = Vector3.Distance(Vector3.zero, pos);

    Debug.LogFormat("{0}--{1}--{2}", m01, m02, m03);
    
    Debug.DrawLine(Vector3.zero, pos);
}

//方向
private void Demo02()
{
    Vector3 pos = this.transform.position;
    Vector3 n01 = pos / pos.magnitude;
    Vector3 n02 = pos.normalized;

    Debug.DrawLine(Vector3.zero, n02, Color.red);
}

 

向量的运算

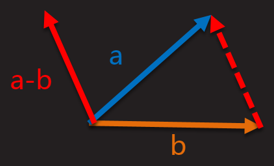
向量相减：等于各分量相加减，应用于计算两点间的距离和相对方向

 

几何意义：向量a与向量b相减，结果理解为以b的终点为始点，以a的终点为终点的向量。方向由b指向a

 

向量相加：等于各分量相加和，应用于物体移动 

 

几何意义：向量a与向量b相加，平移使b的始点与a的终点重合，结果为以a的始点为始点，以b的终点为终点的向量

向量与标量的乘除 

乘法：该向量的各分量与标量相乘；k[xy,z]= [xk,yk,zk]

除法：该向量的各分量与标量相除；[x,y,z]/k = [x/k,y/k,z/k]

几何意义：缩放向量长度  

public Transform t1, t2, t3;

private void Update()
{
    Demo03();
}

//向量运算
private void Demo03()
{
    //t1相对于t2的位置
    //其大小为两点间距离
    Vector3 relativeDirection = t1.position - t2.position;

    //t3沿relativeDirection方向移动
    if (Input.GetKeyDown(KeyCode.A))
    //获取方向向量，避免两物体间距离对速度造成影响
    //t3.Translate(relativeDirection.normalized * 0.5f);
    t3.position+=relativeDirection.normalized;

    Debug.DrawLine(Vector3.zero, relativeDirection);
}

 

三角函数

角的度量方式

PI=180度 1弧度=180度/PI 1角度=PI/180度

角度-->弧度：弧度=角度数*PI/180 

API：弧度=角度数*Mathf.Deg2Rad

弧度-->角度：角度=弧度数*180/PI

API：角度=弧度数*Mathf.Rad2Deg

private void Demo01()
{
    //角度-->弧度：弧度=角度数*PI/180
    float d1 = 60;
    float r1 = d1 * Mathf.PI / 180;
    float r2 = d1 * Mathf.Deg2Rad;
    print("角度-->弧度：" + d1 + "-->" + r1 + "/" + r2);
}

private void Demo02()
{
    //弧度-->角度：角度=弧度数*180/PI
    float r1 = 3;
    float d1 = r1 * 180 / Mathf.PI;
    float d2 = r1 * Mathf.Rad2Deg;
    print("弧度-->角度：" + r1 + "-->" + d1 + "/" + d2);
}

三角函数 

建立了直角三角形中角与边长比值的关系

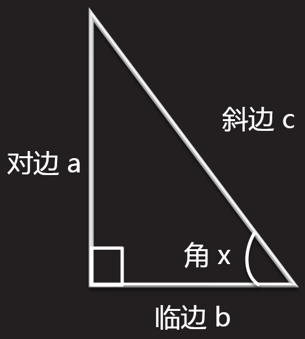
正弦：sin x = a / c

余弦：cos x = b / c

正切：tan x = a / b 

API（以弧度为单位）：

正弦：Mathf.Sin

余弦：Mathf.Cos

正切：Mathf.Tan

反三角函数

反正弦，反余弦，反正切等函数的总称；可用于根据两边长，计算角度

反正弦：arcsin a / c = x

反余弦：arccos b / c = x

反正切：arctan a / b = x;

API（以弧度为单位）：

反正弦：Mathf.Asin

反余弦：Mathf.Acos

反正切：Mathf.Atan

private void Demo03()
{
    //已知角度x，边长b，求边长a
    float x = 50, b = 20;
    float a = Mathf.Tan(x * Mathf.Deg2Rad);

    //已知边长a，边长b，求角度angle
    float angle = Mathf.Atan(a / b) * Mathf.Rad2Deg;

    print(angle);
}

private void Demo04()
{
    //将自身坐标系转换到世界坐标系中
    //Vector3 worldPos = transform.TransformPoint(0, 0, 10);

    //计算物体前方30度，10m远的坐标
    float x = Mathf.Sin(30 * Mathf.Deg2Rad) * 10;
    float z = Mathf.Cos(30 * Mathf.Deg2Rad) * 10;
    Vector3 worldPos = transform.TransformPoint(x, 0, z);
    print(worldPos);
}

Transform.TransformPoint(Vector3 position)：将position从本地空间变换到世界空间