原题链接：Problem - D - Codeforces

题面： 

大概意思就是给你一个数组a和数组b，你自己设计一个数组c，Koxia可以从a[i]、b[i]和c[i]中选一个，而Mahiru只能从另外两个里选一个，问你有多少个数组c一定能使Mahiru选择的数字形成一个1~n的排列。

 思路：

首先我们需要知道，a[i]、b[i]和c[i]中一定要有两个是相同的，并且Koxia必须选择那个和另外两个不同的数（或者三个数都相同了）。这是为什么呢？因为若a[i]、b[i]和c[i]都是不相同的，那么Mahiru的选择的数就不是固定的了，这样就肯定形成不了排列。所以我们要让Mahiru的选择固定下来。

为了使得Mahiru的选择固定下来，三个数中则至少有两个数是一样的，这样子Koxia就可以选择那个不同的数，使得Mahiru的选择固定了。而若a[i]和b[i]原本就一样的话，c[i]可以选任何值，对方案的贡献值为*n，若不一样的话，则c[i]只能等于a[i]或者b[i]。对方案的贡献值可能为*2。为什么是可能呢？因为有时候并不是两个选择都能有相应的答案。

我们在点a[i]与点b[i]之间连一条边，若d能是一个排列，则每个结点都能被恰好被指一次，每个边只能指向一个节点。

以题目中的样例来打个比喻：

3

1 2 2

1 3 3

可以画成下面这样的图

 对于结点2、3，我们有两种选法使得每个结点都能被恰好被指一次

 

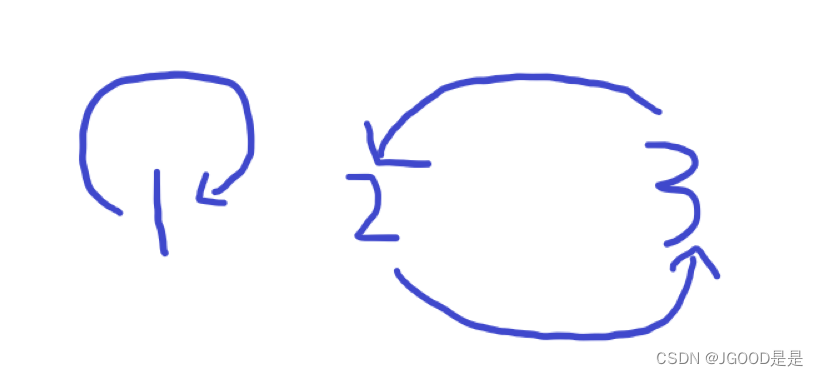
所以对于结点2、3我们有两种选法，而且结点1是一个自环，c[1]在1~3中都可以选，所以对于样例一，我们总共有3*2=6种选法。

而样例中的：

5

3 3 1 3 4

4 5 2 5 5

可以这样画：

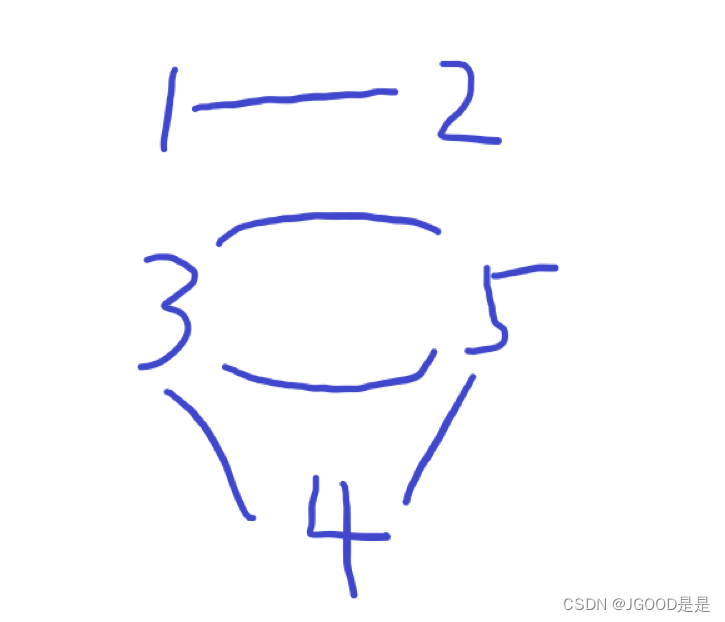
它肯定没有解，这是为什么呢？因为1和2都不可能都选到。相信有一部分同学已经看出来了，若有解，则每个连通块都必须有一个环，也就是每个联通块不能有两个及以上的环（因为若一个连通块形成不了环了，那必然会有某个连通块会多出环来）。

最后在有解的情况下，若结点a[i]=b[i]，则方案数*n，因为c[i]无论怎么选都不会使得本来有解的情况变成无解，所c[i]可以在1~n中任选。若结点a[i]!=b[i]，则看a[i]和b[i]是否在一个环中，若在一个环中，就说明我们可以在这个环中逆时针选一次，顺时针选一次，方案数*2。若无环则方案数不变。

using mint = simpler::modint<998244353>;
int find(int x) {
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void solve() {
	mint ans = 1;
	int n;
	cin >> n;
	FOR(1, n) fa[i] = i, cnt[i] = 0;
	FOR(1, n) cin >> a[i];
	FOR(1, n) cin >> b[i];
	FOR(1, n) {
		int fx = find(a[i]), fy = find(b[i]);
		if (a[i] == b[i]) ans *= n, cnt[fy]++;//若形成自环则方案数*n
		else if (fx == fy) ans *= 2, cnt[fy]++;//若形成环了则方案数*2 
		else  fa[fx] = fy, cnt[fy] += cnt[fx];//若无环则方案数不变 
		if (cnt[fy] > 1) {//判断是否形成了两个及以上的环
			cout << 0 << endl;
			return;
		}
	}
	cout << ans << endl;
}