2022年数维杯数学建模

A题 银行效率评价与破产成因分析

原题再现：

  银行在国家经济社会发展过程中扮演者重要的决策，银行的破产会对企业和个人造成众多不利的影响。相比国内的银行，国际银行的倒闭频次更高，因此国际银行倒闭原因的分析与预测受到众多管理者与学术研究者的广泛关注。附件 1中提供了波兰 2017 年至 2021 年的现存或倒闭银行的 64 项指标数据，各项数据指标具有对应的解释。请你结合这些数据完成以下五项任务：
  任务 1：请你从这 64 项数据中整理出适合的投入产出数据，并对各银行的效率展开对应评价，同时提供银行倒闭效率的分界线；
  任务 2：请利用该 64 项指标对银行倒闭的原因进行挖掘，并提供最为重要的5 项指标数据及其对应的权重；
  任务 3：对任务 1 和任务 2 中的银行倒闭分析结果展开比对分析，同时提出一个精确的倒闭风险预测模型；
  任务 4：你能否从 2021 年银行数据中筛选出最具代表意义的 20 家现存银行和 20 家倒闭银行，并利用这些银行数据对其它银行倒闭风险进行预测；
  任务 5：你能否通过相关理论分析出 2017 年至 2021 年的银行数据中哪些数据可能来自同一家银行，并结合同一家银行的时间序列数据预测哪些银行呈现出了倒闭的趋势。

整体求解过程概述(摘要)

  随着全球经济一体化趋势加剧，金融业所面临的挑战越发明显。许多银行由于不良贷款、坏账等情况激增，导致银行负债乃至破产，为此对其他国家的银行进行效率评价及破产分析，从而避免我国国民经济遭到损失显得至关重要。本文建立5个数学模型进行深入分析研究。
  针对问题 1，首先对附件的数据进行预处理，剔除缺失值占比高的银行数据。而问题1属于提取数据问题，为了整理出合适的投入产出数据，我们建立基于主成分分析法和聚类分析法的银行效率评价模型，利用碎石图、因子荷载象限二维分布图和热力图进行分析，得到 13 个主要指标，并进行银行效率评价，然后利用聚类分析，将 13 个指标的中心值的连线作为银行倒闭效率的分界线。
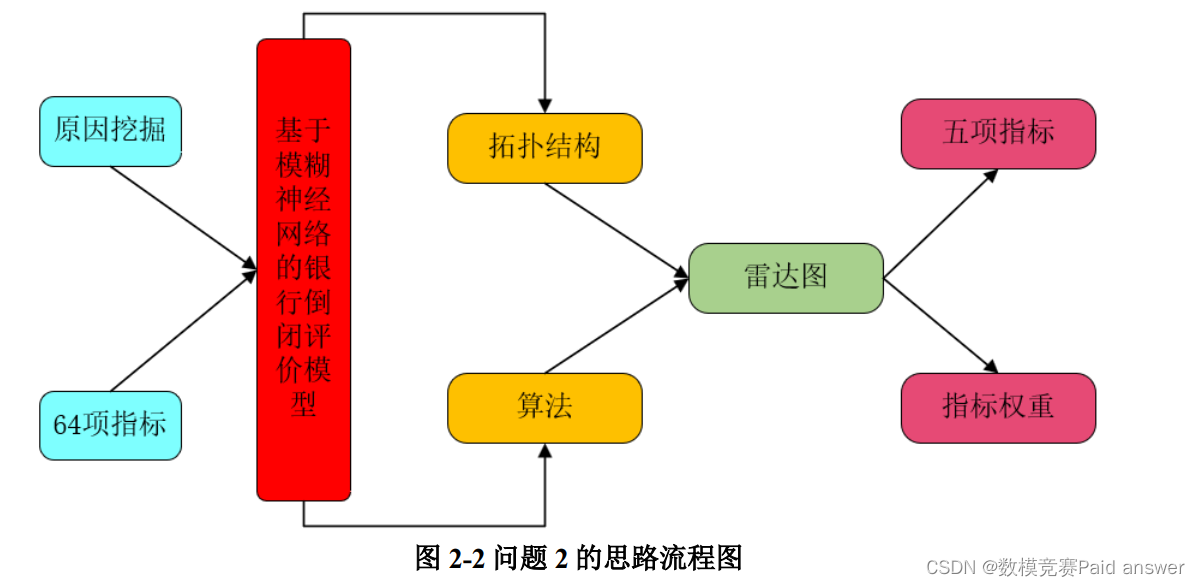
  针对问题 2，是关于数据指标提取问题，为得到最重要的 5 项指标，我们建立基于模糊神经网络的银行倒闭分析模型，结合模糊神经网络拓扑结构图与相关算法进行银行银行倒闭指标的挖掘，根据雷达图找出权重最大的 5 项指标为 X19、X34、X48、X26 和 X44，其权重值依次为 0.0661、0.0424、0.0339、0.0322 、0.0280。
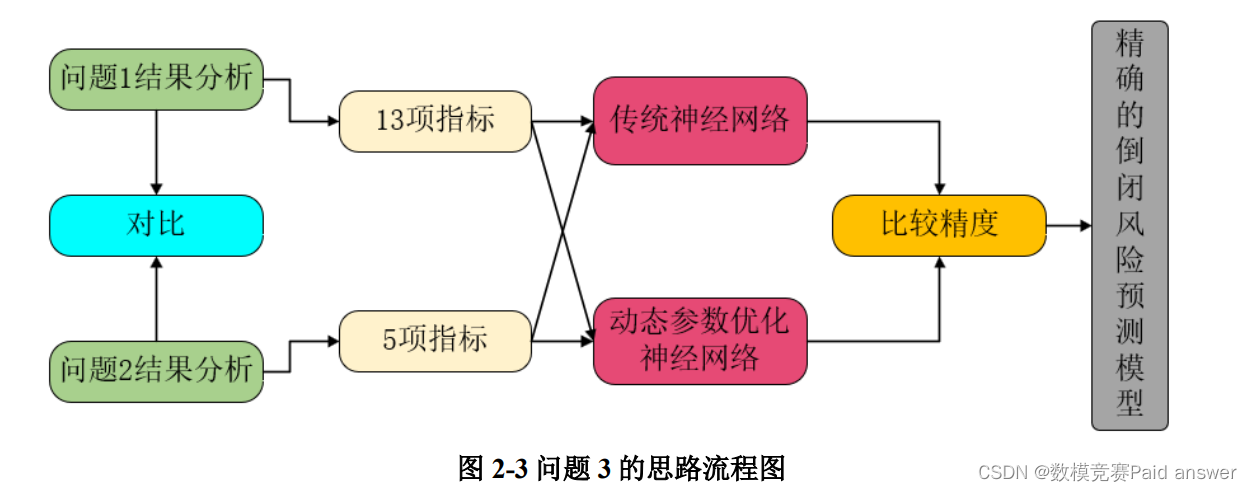
  针对问题 3，首先我们对问题 1 和问题 2 的结果进行对比分析，然后根据 18 个重要指标，建立基于动态参数优化神经网络的银行倒闭风险预测模型，在将传统神经网络和动态参数优化的神经网络精度进行对比后，发现后者预测银行倒闭风险更加准确。
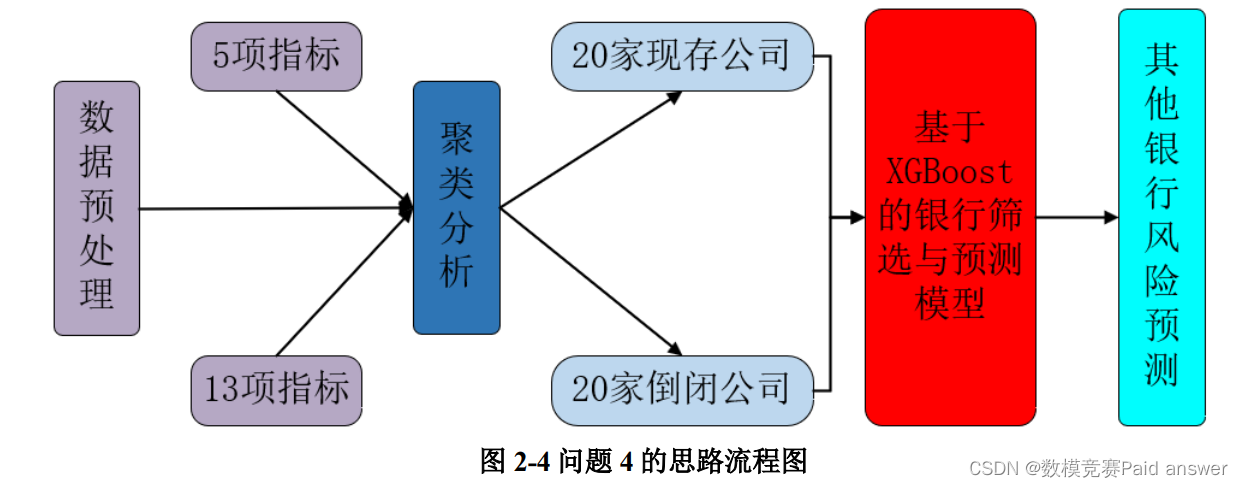
  针对问题 4，是关于数据筛选和预测类问题，为筛选出最具代表意义的 20 家现存银行和 20 家倒闭银行，我们建立基于 XGBoost 的银行筛选与预测模型，在结合聚类分析的方法和问题 1、2 和 3 的结论进行筛选后，通过 SPSSPRO 对其他银行倒闭风险进行了预测。
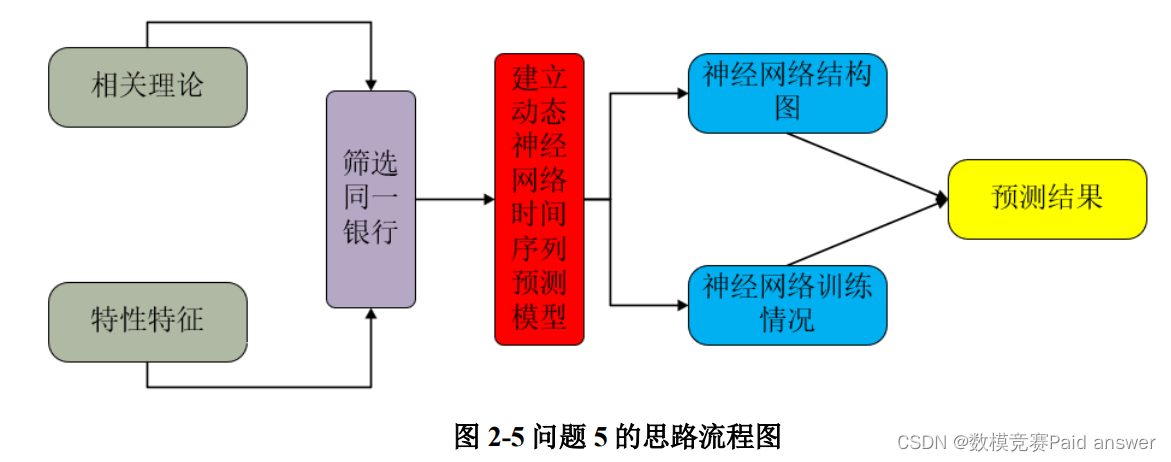
  针对问题 5，我们首先规定同一银行具备三大特征：（1）五年内 64 项指标地数据平均误差不超过 16%；（2）指标变化的范围在 10%以内；（3）指标的波动情况大抵一致。然后结合相关理论，建立动态神经网络时间序列预测模型，经过网络训练发现有324 家银行为同一家银行，其中时间序列预测呈现倒闭趋势的银行有 167 家，未出现倒闭趋势的银行有 157 家。
  最后，我们详细地分析了模型的误差，总结了所建立的模型优缺点，并对模型的发展做出了推广。

问题分析：

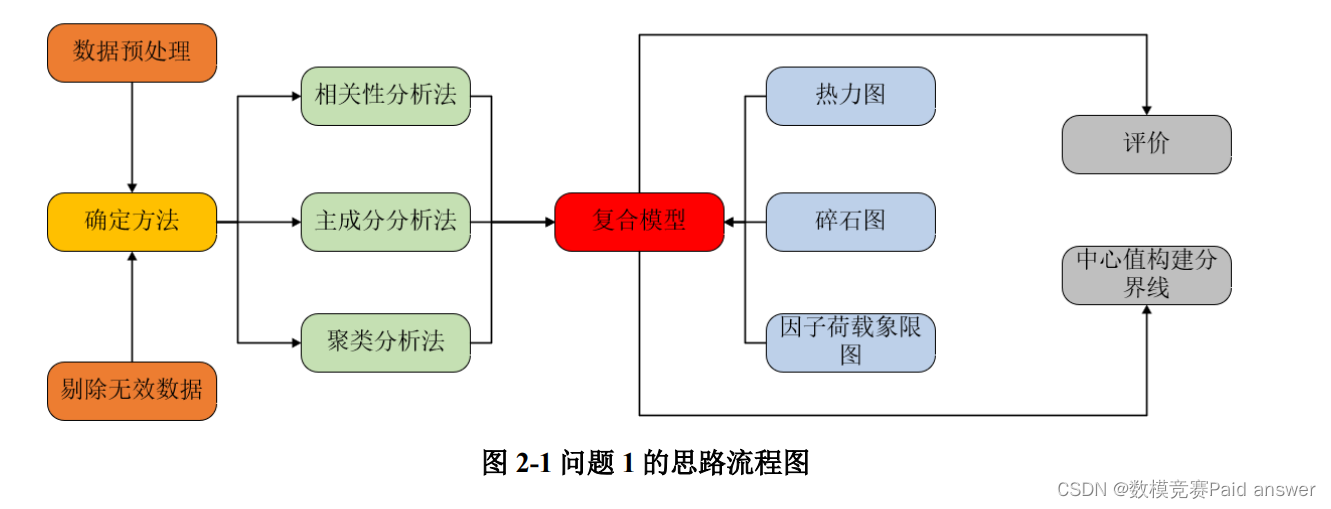
  对于问题 1，整理出合适的投入产出数据，有利于了解银行的经营状况，从而更好做出分析。首先我们对数据进行预处理，剔除缺失值多的银行数据。而问题1属于提取数据问题，对解决这类问题，我们建立基于主成分分析法和聚类分析法的银行效率评价模型，利用碎石图、因子荷载象限二维分布图和热力图进行分析提取主要指标，并进行银行效率评价，然后利用聚类分析，分为两类，求解银行倒闭效率的分界线，具体思路如图 2-1 所示。

  对于问题 2，数据指标提取问题，为得到最重要的 5 项指标，我们建立基于模糊神经网络的银行倒闭评价模型，结合模糊神经网络拓扑结构图与相关算法进行银行银行倒闭指标的挖掘，根据雷达图的结果，最后找出权重最大的 5项指标，具体思路如图 2-2 所示。

  对于问题 3 是一个预测类问题，首先我们对问题 1 和问题 2 的结果进行分析，然后根据以上两个问题的重要指标，建立基于动态参数优化神经网络的银行倒闭风险预测模型进行求解，并对传统神经网络和动态参数优化的神经网络精度进行对比后，利用后者预测银行倒闭风险，具体思路如图 2-3 所示。

  对于问题 4，属于数据筛选和预测类问题，为筛选出最具代表意义的 20 家现存银行和 20 家倒闭银行，我们建立基于 XGBoost 的银行筛选与预测模型，利用聚类分析法和问题 1、2 和 3 的结论进行筛选，并通过 SPSSPRO 根据 XGBoost 模型，结合 40 家银行的数据预测其它银行，具体思路如图 2-4 所示。

  对于问题 5，属于数据筛选和预测类问题，我们首先规定同一银行具备的特征，然后根据特征情况进行筛选，然后建立动态神经网络时间序列预测模型，预测同一银行的倒闭趋势，具体思路如图 2-5 所示。

模型假设：

  1. 假设题目所给的银行 64 个指标的数据真实可靠；
  2．假设银行倒闭的因素取决于所给的 64 个指标，且无其他因素影响。
  3．假设数据处理所剔除的数据不影响 5 个问题的分析；
  4．假设最具代表性的银行具有共同的特性；
  5．假设问题 5 可以通过前 4 个问题的结果进行预测。

数据的预处理

  本题中的共有五年的数据，其中第一年数据包含预测期第一年的财务比率和相应的类别标签，表示 5 年后的破产状态。该数据包含 7027 个实例（财务报表），271 个代表破产的银行，6756 个在预测期内没有破产的银行。第二年的数据包含预测期第二年的财务比率和相应的类标签，表示 4 年后的破产状态。数据包含 10173 个实例（财务报表），400 个代表破产的银行，9773 个在预测期没有破产的银行。第三年的数据包含预测期第三年的财务比率和相应的类标签，表示 3 年后的破产状态。数据包含 10503 个实例（财务报表），495个代表破产的银行，10008个在预测期没有破产的银行。第四年的数据包含 9792 个实例（财务报表），515 个代表破产的银行，9277 个在预测期内没有破产的银行。第五年的数据包含预测期第 5 年的财务比率和相应的类标签，表示 1 年后的破产状态。数据包含 5910 个实例（财务报表），410 个代表破产的银行，5500 个在预测期没有破产的银行。我们将这些数据进行汇总，预处理后发现，存在数据缺失，如图5-1、图 5-2 和图 5-3 所示。


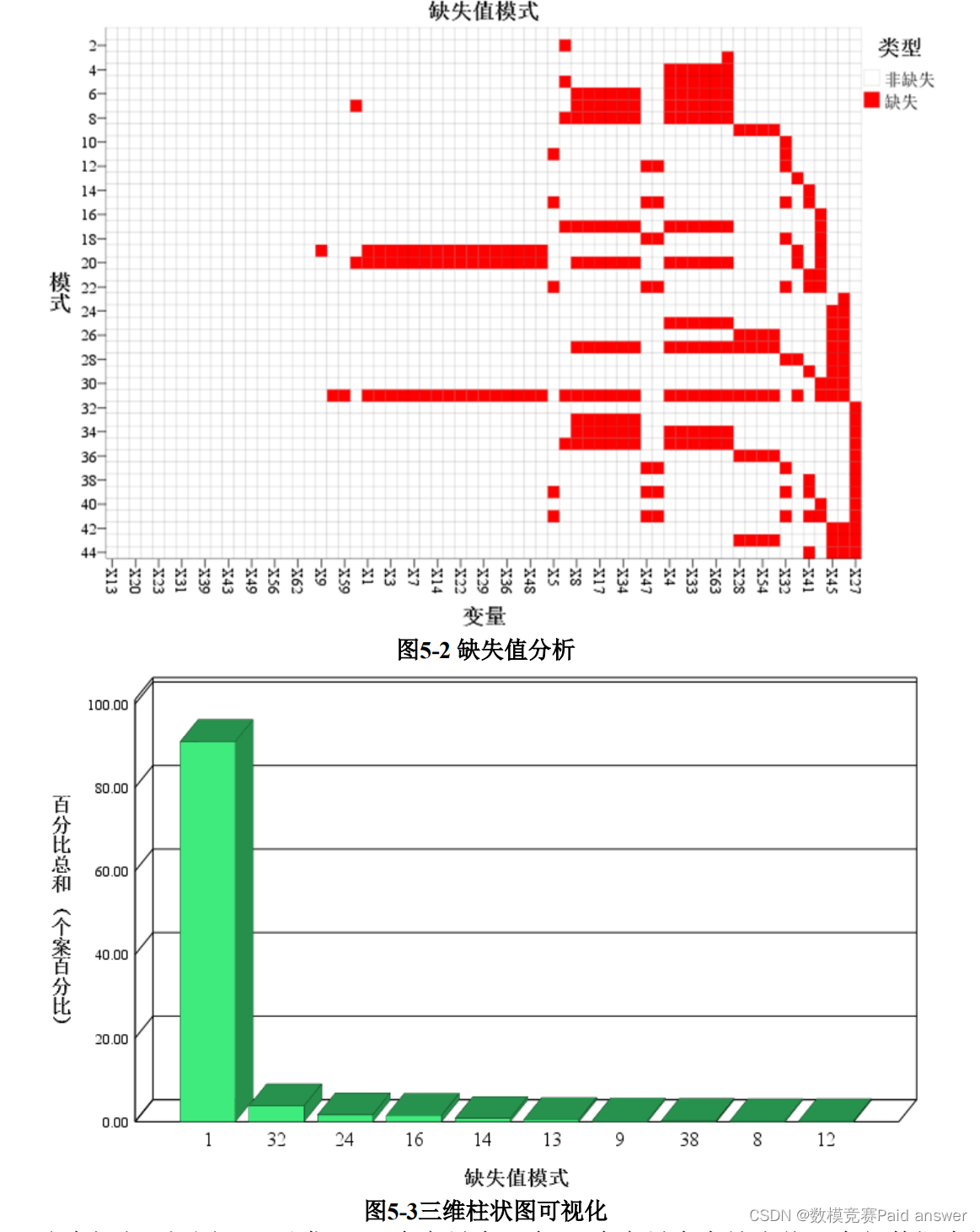
  通过上述三幅图，可以发现 65 个变量中，有 18 个变量存在缺失值，全部数据中缺失数据占 0.322%，由于部分银行缺失数据较多，我们选择将其剔除，不予考虑。

模型的建立与求解

基于主成分分析法和聚类分析法的银行效率分析模型的建立

  在研究波兰各个银行的效率评价问题研究上，需要将 64 类指标进行分类，挖掘出合适的投入指标和产出指标，而主成分分析法和聚类分析法刚好通过全面地进行分析比较符合题目要求，所以我们建立基于主成分分析法和聚类分析法的银行效率评价模型进行研究。

主成分分析法

  由于所给数据缺乏一定的合理性，而主成分分析法是通过降维处理，将原始指标转化为少数几个综合指标进行分析，派出了不确定性。另外本题中的原始指标达到了64 个，指标数量多、相关关系复杂，因此选取主成分妇女洗发，可以在最大限度上保留原始指标信息基础上，进行降维处理，从而得到具有代表性的指标。

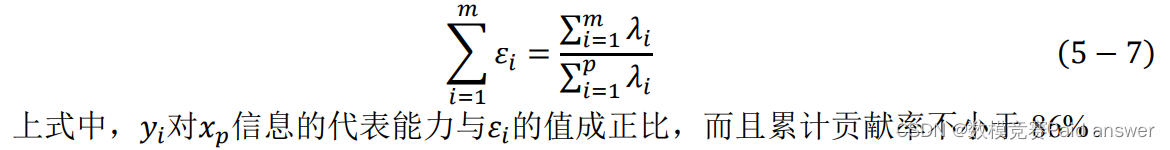
聚类分析方法

  聚类分析法是常用的数据分析方法，根据指标的特性进行分类，从而减少研究指标的数量，具有较强的科学性，避免了认为因素对定性分析的影响。

基于主成分分析法和聚类分析法的银行效率分析模型的求解

  根据上述所建立的模型，利用 SPSSPRO 软件进行求解，其求解步骤为：
  1）进行 KMO 和 Bartlett 的检验，判断是否可以进行主成分分析。 对于 KMO 值：0.8 上非常合适做主成分分析，0.7-0.8 之间一般适合，0.6-0.7 之间不太适合，0.5-0.6 之间表示差，0.5 下表示极不适合，对于 Bartlett 的检验（p < 0.05,严格来说 p < 0.01），若显著性小于 0.05 或 0.01，拒绝原假设，则说明可以做主成分分析，若不拒绝原假设，则说明这些变量可能独立提供一些信息，不适合做主成分分析;
  2）通过分析方差解释表格和碎石图，确定主成分的数量方差解释表格主要是看主成分对于变量解释的贡献率（可以理解为究竟需要多少主成分才能把变量表达为100%），如果太低（如低于 60%）则需要调整主成分数据;碎石图的作用是根据特征值下降的坡度来确认需要选择的主成分个数，这两者结合可用于确认或调整主成分个数;
  3）通过分析主成分载荷系数与热力图，可以分析到每个主成分中隐变量的重要性;
  4）基于主成分载荷图通过将多主成分降维成双主成分或者三主成分，通过象限图的方式呈现主成分的空间分布。如果提取2个主成分时，无法呈现三维载荷主成分散点图，如果提取 1 个主成分时，无法显示主成分象限图;
  5）通过分析成分矩阵，得出主成分成分公式与权重;
  6）输出主成分分析法综合得分。

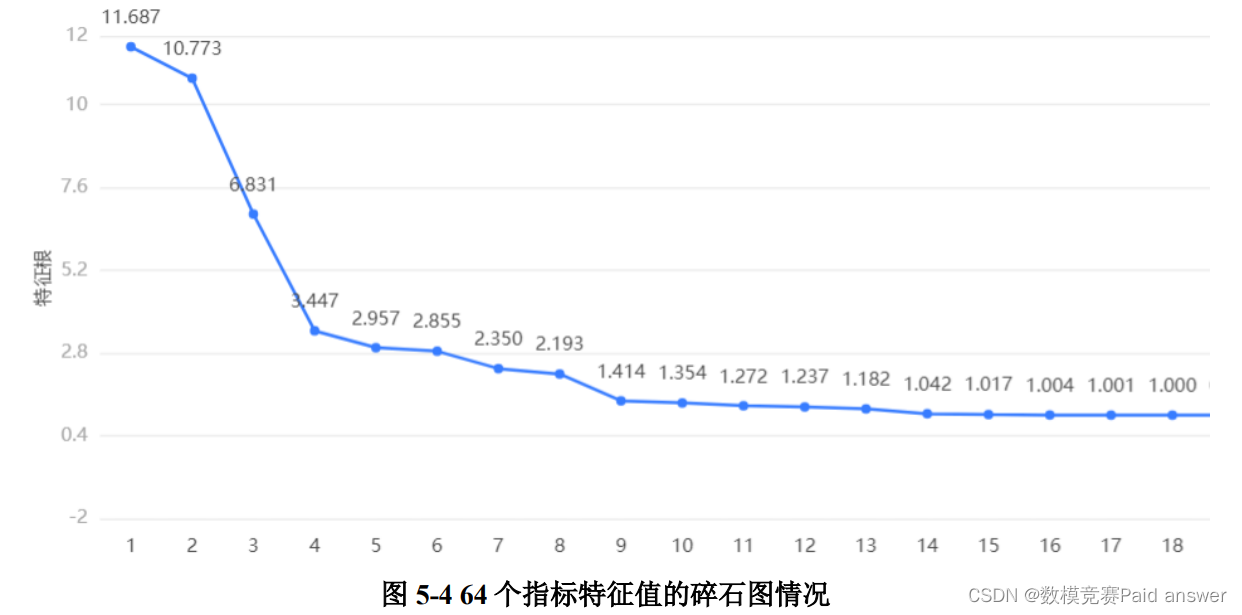
  从图 5-4，可以清楚地发现，通过主成分分析法，对特征值进行重要性分析，排名前八的指标特征值明显比其他指标地特征值大，分别为 11.687、10.773、6.831、3.447、2.957、2.855、2.350、和 2.193，同样可以根据特征值下降的坡度得到需要选择的主成分个数为8个。由于前四个主成分特征值相比其他而言更为显著，所以本题中对银行投入和产出的数据指标为 4 种主成分。

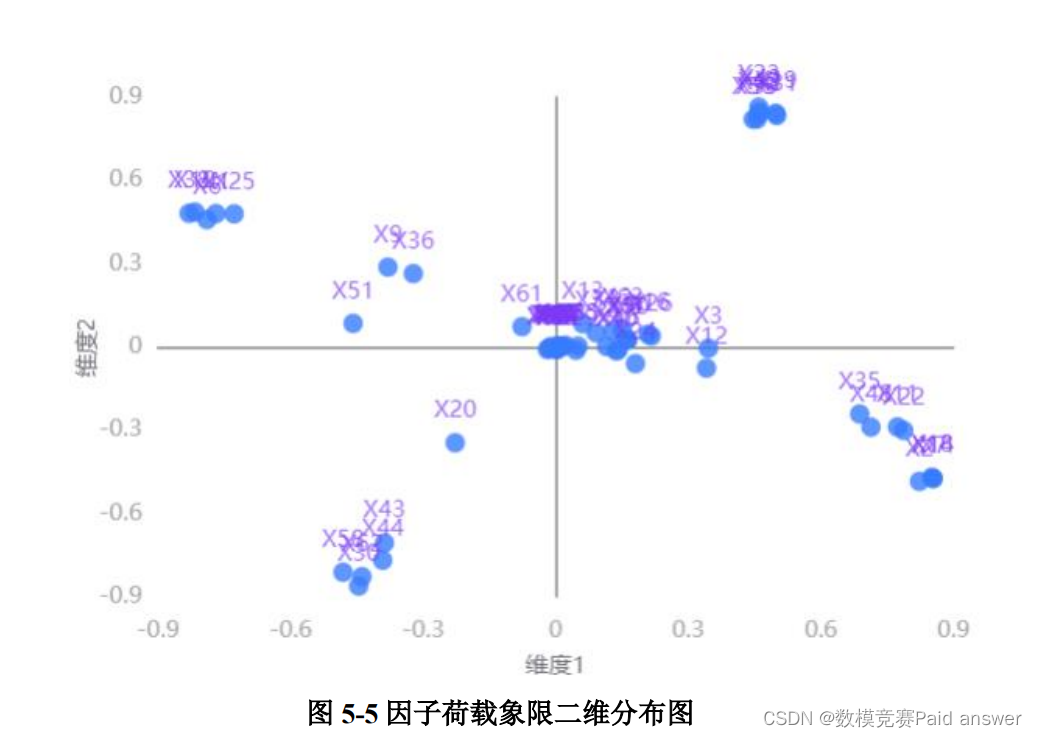
  根据图 5-5，通过象限图的方式呈现主成分的空间分布。由于我们提取的主成分为4 个，所以可以直接呈现二维载荷主成分散点图，从而得到第一象限分布指标数量最多，第二象限和第四象限次之，第三象限最少。根据上述情况，我们得到主成分的权重分布结果，如表 5-1 所示。

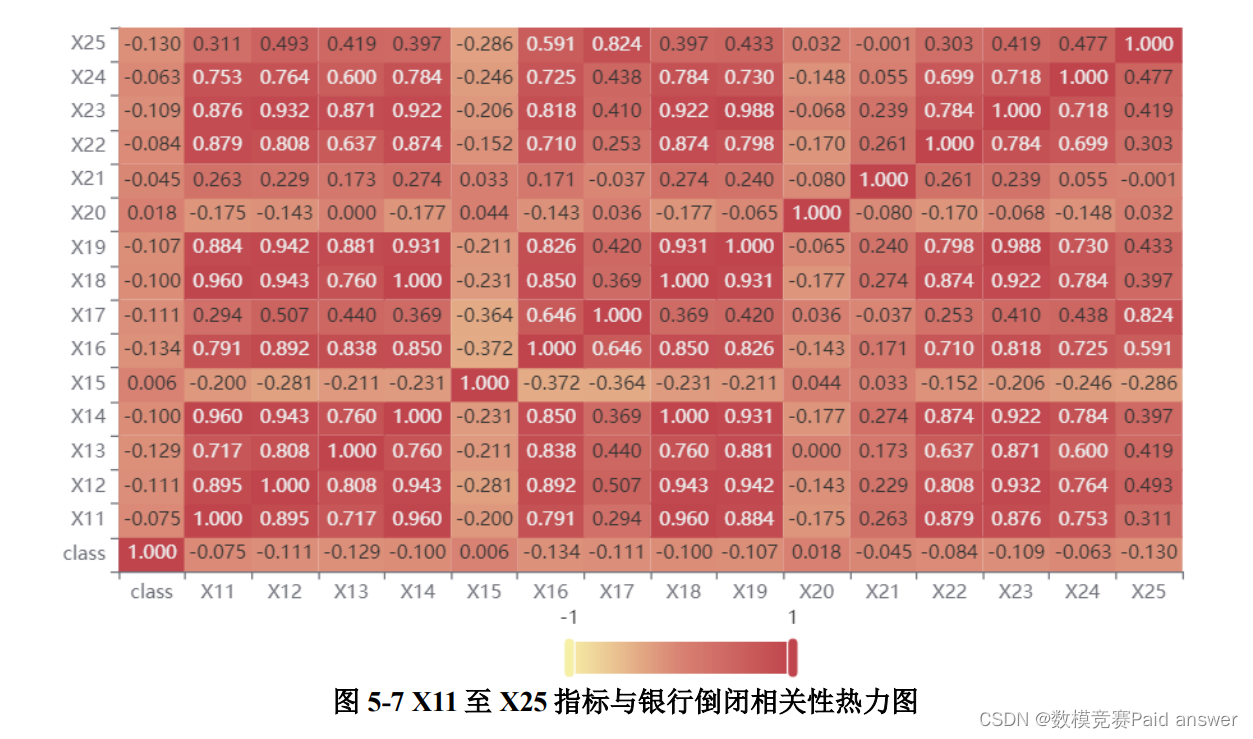
  由图 5-7，可知 X13 的相关性为-0.129, X16 的相关性为-0.134,存在较强的相关性。X12 的相关性为-0.111、X13 的相关性为-0.129、X17 的相关性为-0.111、X19 的相关性为-0.107、X23 的相关性为-0.109、X25 的相关性为-0.130、X39 的相关性为-0.110、X46的相关性为-0.110。
  根据热力图的相关性可以发现 X1、X2、X6、X8、X12、X13、X16、X17、X19、X23、X25、X39 和 X46，一共 13 项与银行是否倒闭存在较强的相关性，我们对着 13项进行聚类分析，且分为两类。分析步骤为：
  1）根据字段进行聚类类别差异性分析;
  2）根据聚类汇总分析各聚类类别的频数;
  3）根据数据集聚类标注可以知道每一个样本数据被分到哪个类别;
  4）聚类中心坐标可以用于分析各样本与中心点的距离;
  5）对分析进行综述。

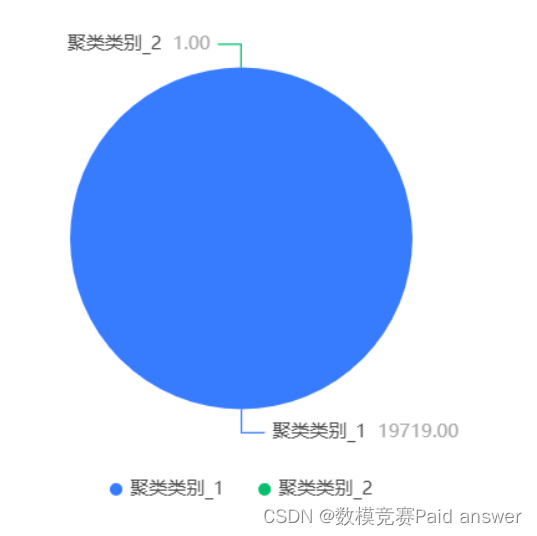
  由上图可以得知，聚类结果共分为 2 类， 聚类类别 1 的频数为 19719，所占百分比为 99.995%； 聚类类别 2 的频数为 1，所占百分比为 0.005%，所得到的聚类中心点坐标如表 5-2 所示。

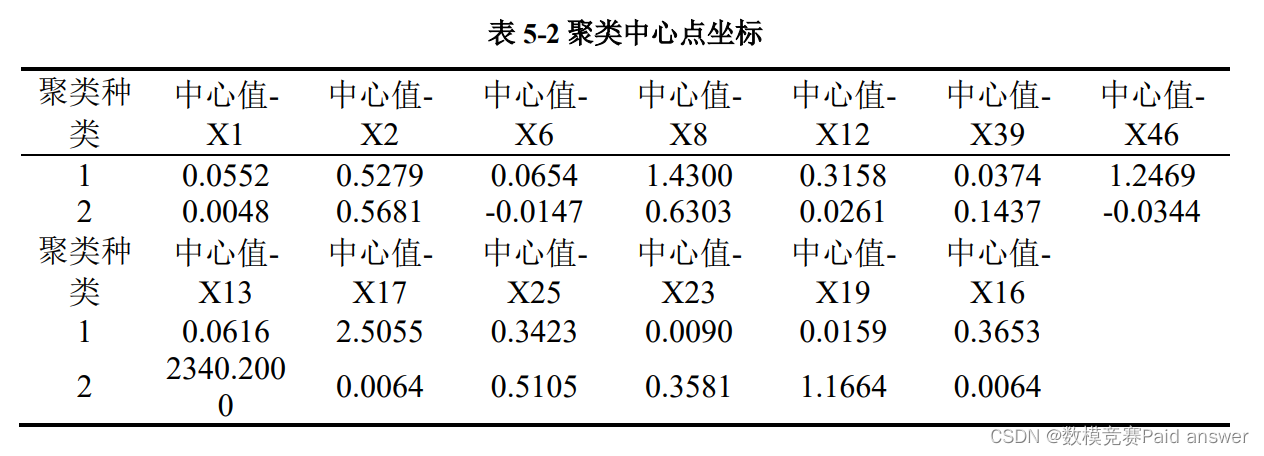
  对于问题一，为整理出适合银行的投入产出数据，我们基于主成分分析法和相关性分析法进行建模求解，通过碎石图、因子荷载象限二维分布图和相关性热力图可视化得到适合的指标为 X1 净利润/总资产、X2 负债总额/资产总额、X6 留存收益/总资产、X8 权益的账面价值/总负债、X12 毛利/短期负债、X13(毛利+折旧)/销售额、X16(毛利润+折旧)/总负债、X17 总资产/总负债、X19 毛利/销售额、X23 净利润/销售额、X25(权益+股本)/总资产、X39 销售利润/销售额和 X46(流动资产-存货)/短期负债，一共 13 项
可以代表银行的投入产出数据，具体评价情况见支撑材料。为了计算银行倒闭效率的分界线，我们利用聚类分析方法进行分析求解，设置以银行是否倒闭作为类别，将 64 种指标分为两类，计算各样本与中心点的距离，即为银行倒闭效率的分界线，结果可视化如图 5-9 所示。

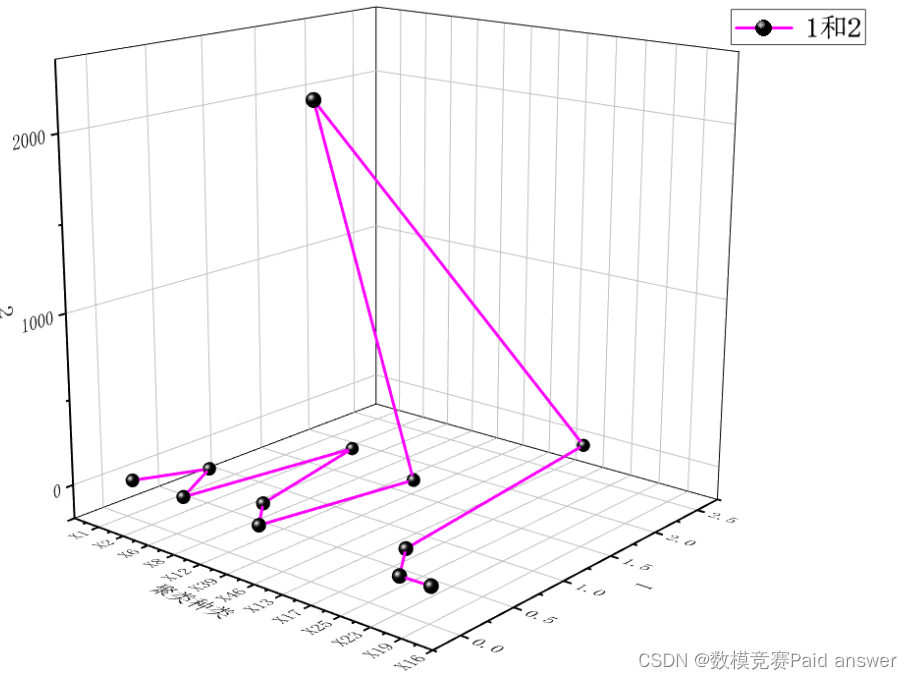
基于动态参数优化神经网络的银行倒闭风险预测模型的求解

  我们将处理后的数据进行汇总，在任务 1 中得到适合投入和产出的指标为 X1 净利润/总资产、X2 负债总额/资产总额、X6 留存收益/总资产、X8 权益的账面价值/总负债、X12 毛利/短期负债、X13(毛利+折旧)/销售额、X16(毛利润+折旧)/总负债、X17 总资产/总负债、X19 毛利/销售额、X23 净利润/销售额、X25(权益+股本)/总资产、X39 销售利润/销售额和 X46(流动资产-存货)/短期负债，一共 13 项，在任务 2 中得到最为重要的五项指标为 X19 毛利/销售额、X34 营业费用/总负债、X48 EBITDA (经营活动的利润-折扣)/总资产、X26 (净利润+折扣)/总负债和 X44 (应收账款* 365)/销售额。所以在这里我们将 18 项指标数据数据带入上述模型，通过 SPSSPRO 软件进行分析预测。具体步骤如下：
  (1)通过训练集数据来建立动态参数优化神经网络回归模型。
  (2)将建立的动态参数优化神经网络模型应用到训练、测试数据，得到模型评估结果。
  (3)由于动态参数优化神经网络具有随机性，每次运算的结果不一样，若保存本次训练模型，后续可以直接上传数据代入到本次训练模型进行计算预测。

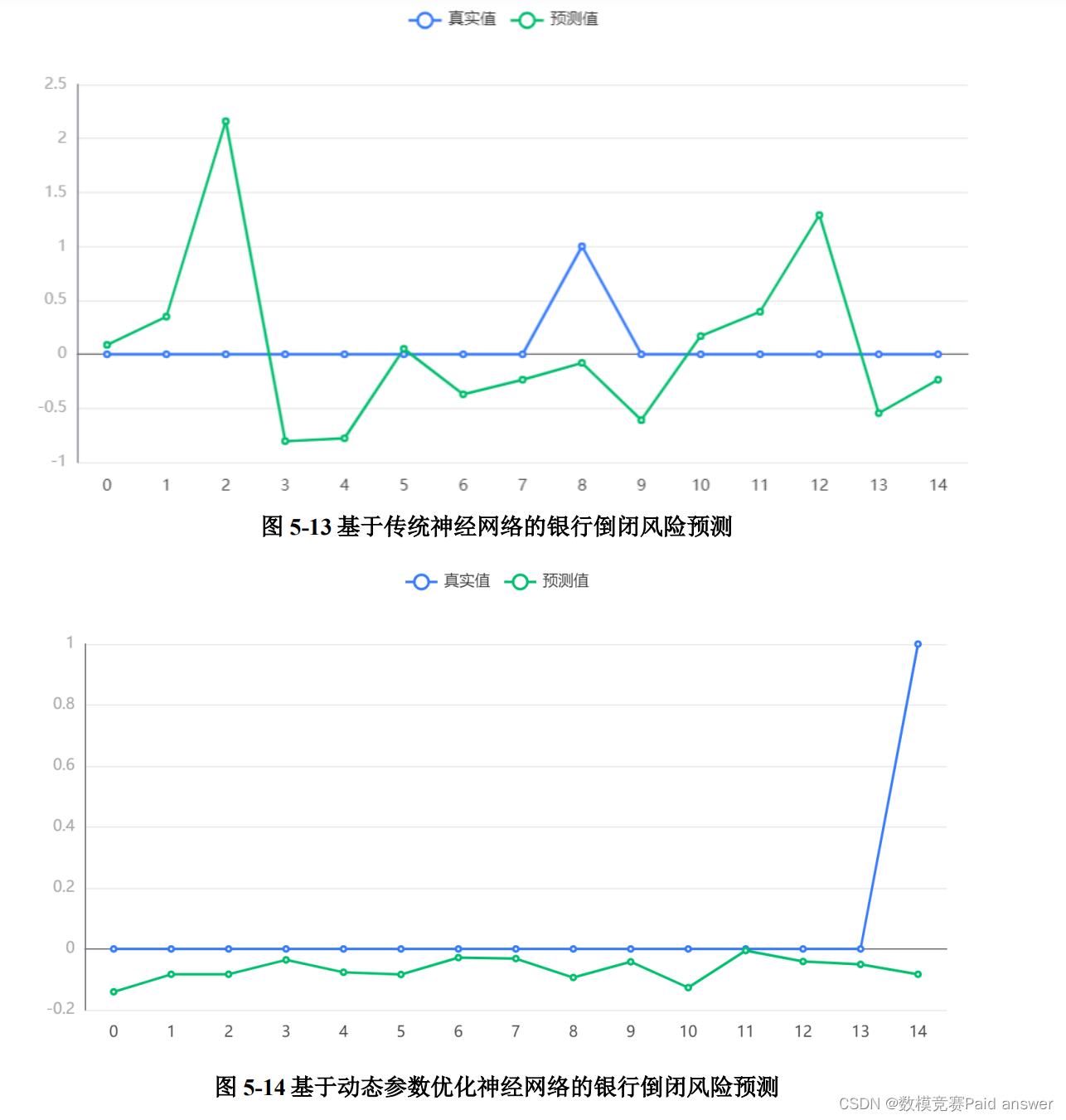
  通过图 5-13 和图 5-14. 可以得到传统神经网络模型和动态参数优化神经网络模型的预测结果，通过图示发现，经过动态参数优化的神经网络预测精度远远比传统神经网络的精度高，两者精度对比如表 5-5 所示。


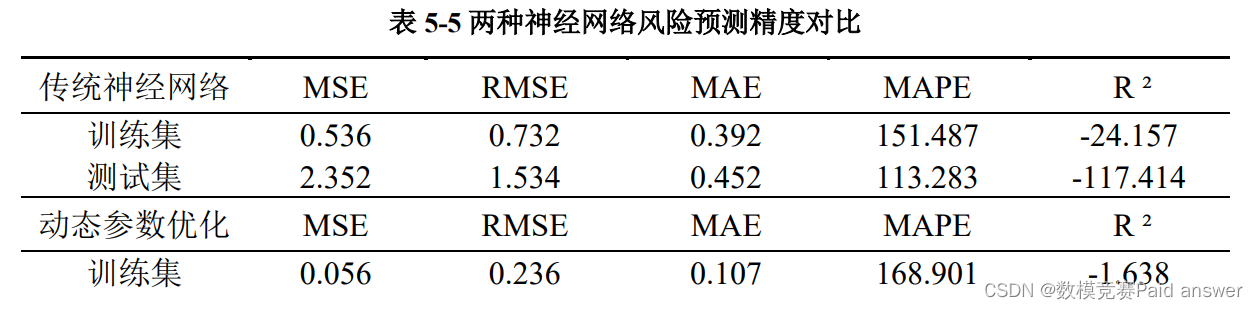
  针对问题 3，我们总结问题 1 和问题 2 并进行对比分析发现影响银行破产的因素共有 18 个，分别为 X1净利润/总资产、X2负债总额/资产总额、X6留存收益/总资产、X8权益的账面价值/总负债、X12 毛利/短期负债、X13(毛利+折旧)/销售额、X16(毛利润+折旧)/总负债、X17 总资产/总负债、X19 毛利/销售额、X23 净利润/销售额、X25(权益+股本)/总资产、X39 销售利润/销售额和 X46(流动资产-存货)/短期负债、X19 毛利/销售额、X34 营业费用/总负债、X48 EBITDA (经营活动的利润-折扣)/总资产、X26 (净利润+折扣)/总负债和 X44 (应收账款*365)/销售额。影响因素具有多角度、多层次、集中性的特征。
  之后我们通过 SPSSPRO 软件进行模型求解，将 18 项影响指标作为自变量、是否破产作为因变量，进行预测分析，并对比传统神经网络预测和动态参数优化的神经网络预测精度，发现动态参数优化的神经网络对银行倒闭风险预测更为准确，说明所建立的模型具有准确性、可靠性、合理性。

论文缩略图：

程序代码：

from fileinput import filename
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier as KNN
# 导入数据
df = pd.read_excel('附件（数据处理后 5 年合集）.xlsx')
data = df.iloc[:1:65] #X
target = df.iloc[:65:66] #y
X_train,X_test,y_train,y_test = train_test_split(data,target,test_size=0.2,random_state=0)
# K 值为 1，模型训练
knn = KNN(n_neighbors=1)
knn.fit(X_train,y_train)
# 模型预测，模型评估
y_pred = knn.predict(X_test)
knn_c = round(knn.score(X_test,y_test),2)
print("Test set score:",knn_c)
#Test set score:0.95
#持久化模型
import joblib
filename = 'KNN_model.sav' joblib.dump(knn,filename)
''' 以下为 k 近邻算法与其他算法的对'''
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(penalty='l2')
clf.fit(X_train, y_train)
LogisticRegression_c = round(clf.score(X_test,y_test),6)
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=8)
clf.fit(X_train, y_train)
RandomForestClassifier_c = round(clf.score(X_test,y_test),6)
from sklearn.svm import SVC
clf = SVC(kernel='rbf', probability=True)
clf.fit(X_train, y_train)
SVC_c = round(clf.score(X_test,y_test),6)
from sklearn import tree
clf = tree.DecisionTreeClassifier()
clf.fit(X_train, y_train)
DecisionTreeClassifier_c = round(clf.score(X_test,y_test),6)
print(LogisticRegression_c,RandomForestClassifier_c,SVC_c,DecisionTreeClassifier_c)''' def add_labels(rects): #添加数据标签
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x() + rect.get_width()/2, height, height, ha='center', va='bottom')
rect.set_edgecolor('white')
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei' plt.rcParams['axes.unicode_minus'] = False
xz = ['K 近邻','逻辑回归','随机森林','支持向量机','决策树']
yz = [0.95,0.945,0.948,0.950,0.942]
bar = plt.bar(xz,yz,width=0.5,color=['skyblue','tomato','peru','tan','grey'])
add_labels(bar)
plt.xlabel('不同的分类算法')
plt.ylabel('scores')
plt.show()