目录
问题 A: 二叉树的性质
问题 B: 二叉树的节点
问题 C: 满二叉树
问题 D: 完全二叉树的节点序号
-----------------------------------分割线------------------------------------------
问题 E: 二叉树的深度
问题 F: 数据结构作业04 -- 二叉树的输入
递归版
迭代版
问题 G: 给定前序遍历序手动构造二叉树-附加代码模式
问题 A: 二叉树的性质
答案非常简单就是输出n-1
但怎么证的呢?
我们不妨先论证一下总的度数和节点数的关系(这里的度指的是子节点数)
最开始我们的树只有一个根节点,而每派生出一个“度”,也就派生出了一个子节点
所以在这之后派生出的总度数量是等于所以子节点数量的
在加上根节点,也就得到了下面式子
节点总数=总度数+1
而左边节点度数可以写成 度为0的节点+度为1的节点+度为2的节点
右边可以写成 2*度为2的节点+1*度为1的节点+1
上式即为 度为0的节点+度为1的节点+度为2的节点= 2*度为2的节点+1*度为1的节点+1
两边一合并
度为2的节点+1=度为0的节点
也就证出来了
代码如下
cpp
int n;
cin>>n;
cout<<n-1<<endl;python
n = int(input())
print(n-1)问题 B: 二叉树的节点
这个应该不难想
二叉树的深度取决于最深的节点
最少节点我们只要一条路走到黑或者之字形走,如下图
这样最少节点数就等于深度

(题外话)
也就是说基于二叉树实现的搜索树最坏情况会退化为链表,而在单链表中查找和指定删除都为
边缘性能很差,这也就有了之后AVL,红黑树的故事
最多也很简单
只需要每层都满节点就好了
也就是
也就等于
cpp代码
int n;
cin>>n;
cout<<n<<' '<<pow(2,n)-1;python代码
h=int(input())
ma = pow(2,h)-1
print(h,ma)问题 C: 满二叉树
这道题同上了
满二叉树就是节点最多的时候
判断即可
cpp代码
int h,n;
while(cin>>h>>n)
{
if (n==pow(2,h)-1) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}python代码
while 1:
h,n=map(int,input().split())
if pow(2,h)-1 == n:
print('YES')
else:
print('NO')问题 D: 完全二叉树的节点序号
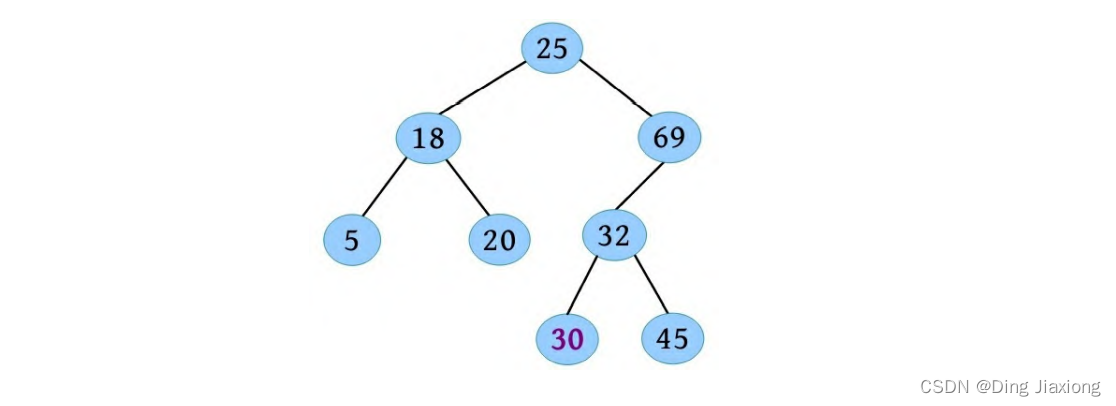
我们用数组在存这种二叉堆结构有一个默认的方式,例如存线段树
左儿子等于父亲*2,右儿子等于父亲*2+1
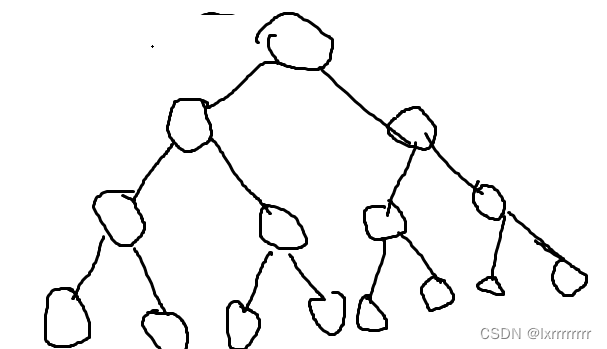
例如存一棵value值如下图的7个节点的满二叉树
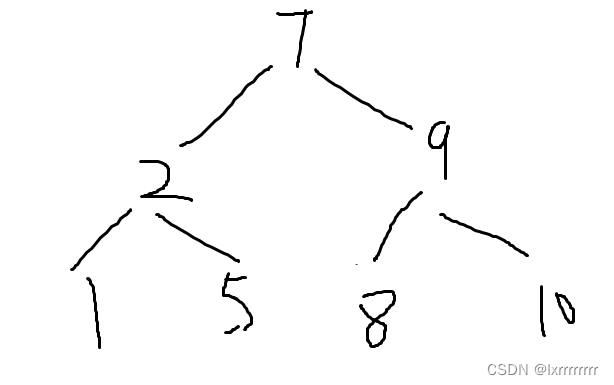
在数组中为
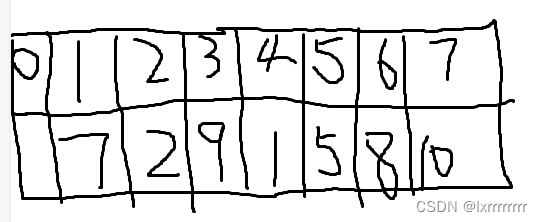
这样a[2]的儿子就是left:a[2*2],right:a[2*2+1]
也就是a[4]和a[5]
这题下标是从0开始,加个偏移量即可
代码如下
int n;
while(cin>>n){
if(n==0) cout<<"-1 1 2\n";
else cout<<(n-1)/2<<" "<<2*n+1<<" "<<2*n+2<<'\n';
}-----------------------------------分割线------------------------------------------
以下二叉树的前中后序遍历
思路详解见(2条消息) (数据结构)如何手搓一棵二叉树?_lxrrrrrrrr的博客-CSDN博客
我们只要实现一个简单的就好
问题 E: 二叉树的深度
先建树,在找深度
建树:他提供带虚节点前序遍历,前序遍历是 根左右
所以我们按照根左右的方式重构树即可,遇到虚节点时结束,代表当前点无节点
找深度时每个节点的dep=max(dep[left],dep[right])+1
从底层节点递归上来即可
代码如下
#include<bits/stdc++.h>
using namespace std;
int ind;
class node{
public:
char data;
int dep;
node* left;
node* right;
};
class bintree{
public:
node* __root;
void createtree(node* &T,string s);
int updatadep(node *T);
};
void bintree::createtree(node* &T,string s){
char data=s[ind];
ind++;
if(data=='#'){
T=nullptr;
}
else{
T=new node;
T->data=data;
createtree(T->left,s);
createtree(T->right,s);
}
}
int bintree::updatadep(node *T){
int L,R;
if(T!=NULL){
L=updatadep(T->left);
R=updatadep(T->right);
T->dep=L>R?L+1:R+1;
return T->dep;
}
return 0;
}
signed main(){
bintree tree;
string str;
int T;
cin>>T;
while(T--){
cin>>str;
bool fl=false;
for(auto t:str){
if(t!='#'){
fl=true;
break;
}
}
if(!fl){cout<<"0\n";continue;}
ind=0;
tree.createtree(tree.__root,str);
cout<<tree.updatadep(tree.__root)<<'\n';
}
}问题 F: 数据结构作业04 -- 二叉树的输入
建树前一道题已经建过了
这里主要说下中后序遍历
中序遍历我给出了两种方式
递归版和迭代版
递归版
中序遍历是按照 左--根--右 的方式遍历
递归版写起来特别简单

这样在回溯的时候就会按照中序遍历遍历这棵树
前后序遍历的递归版也就是调换一下顺序
迭代版
同样是从根节点开始,不断地沿着左子树向下走。不同的是,这里向下行进的过程中不能访问当前结点,只有等到当前结点的左子树完成访问时,才能轮到当前结点,因此想到引入一个栈来实现延迟缓冲的功能。走到最左侧的第一个没有左子树的叶子结点时,没有左子树也相当于已经完成了左子树的访问,于是随后便访问当前结点x,然后转入到x的右子树。
当x的右子树完成访问时,即标志着以x为根的子树访问完毕,随机访问x的父亲结点,然后访问x的父亲的右子结点。x的右兄弟结点访问完毕时,即标志着以x的父亲的根的子树访问完毕,随即访问x父亲的父亲,然后是x父亲的父亲的父亲...
后序遍历的详解去看(2条消息) (数据结构)如何手搓一棵二叉树?_lxrrrrrrrr的博客-CSDN博客
goAlongLeft函数的作用是对于每一个节点,一直向左走,这一条左链都压入栈
具体实现:对于每一个节点,先一直向左走,将他的所有左儿子都压入栈,之后每一个左儿子
按顺序出栈,遍历此节点,再遍历此节点的右节点,之后下一个左儿子出栈.....
代码如下:
#include<bits/stdc++.h>
using namespace std;
int ind;
class node{
public:
char data;
node* left;
node* right;
};
class bintree{
public:
node* __root;
void createtree(node* &T,string s);
void visit(node* T){if(T->data!='#') cout<<T->data;}
void inorder(node* T);
void postorder(node* T);
void levelorder(node* T);
void goalongleft(stack<node*> &S,node* now);
void inorder_it(node* T);
};
void bintree::createtree(node* &T,string s){
char data=s[ind];
ind++;
if(data=='#'){
T=nullptr;
}
else{
T=new node;
T->data=data;
createtree(T->left,s);
createtree(T->right,s);
}
}
void bintree::inorder(node* T){
if(T!=nullptr){
inorder(T->left);
visit(T);
inorder(T->right);
}
}
void bintree::goalongleft(stack<node*> &S,node* now){
node* curr=now;
while(curr!=nullptr){
S.push(curr);
curr=curr->left;
}
}
void bintree::inorder_it(node* T){
stack<node*> S;
node* curr=T;
while(1){
goalongleft(S,curr);
if(S.empty()) break;
curr=S.top();
S.pop();
visit(curr);
curr=curr->right;
}
}
void bintree::postorder(node* T){
if(T!=nullptr){
postorder(T->left);
postorder(T->right);
visit(T);
}
}
void bintree::levelorder(node* T){
queue<node*> q;
q.push(this->__root);
while(!q.empty()){
node* top=q.front();
q.pop();
visit(top);
if(top->left) q.push(top->left);
if(top->right) q.push(top->right);
}
}
signed main(){
bintree tree;
string str;
while(cin>>str){
bool fl=false;
for(auto t:str){
if(t!='#'){
fl=true;
break;
}
}
if(!fl){cout<<"\n";continue;}
ind=0;
tree.createtree(tree.__root,str);
tree.inorder(tree.__root);
cout<<" ";
// tree.inorder_it(tree.__root);
// cout<<endl;
tree.postorder(tree.__root);
cout<<" ";
tree.levelorder(tree.__root);
cout<<'\n';
}
}问题 G: 给定前序遍历序手动构造二叉树-附加代码模式
随便编一个就行
using namespace std;
struct BiNode
{
string data;
BiNode *lchild, *rchild;
};
typedef BiNode *BiTree;
int InitBiTree(BiTree &T)
{
T = NULL;
return 0;
}
void ManuallyCreateTree(BiTree & T){
T = new BiNode();
T->data = "a";
BiNode* n1 = new BiNode();
n1->data = "b";
BiNode* n2 = new BiNode();
n2->data = "c";
T->lchild = n1;
T->rchild = n2;
BiNode* p = new BiNode();
p->data = "d";
n1->lchild = p;
BiNode* p1 = new BiNode();
p1->data = "e";
n1->rchild = NULL;
n2->lchild = p1;
BiNode* p2 = new BiNode();
p2->data = "f";
n2->rchild = p2;
} C语言毕竟不是面向过程的语言,用C写这种数据结构简直坐牢
毕竟高内聚低耦合的cpp写出来很养眼