【PDPTW】python调用guribo求解PDPTW问题（Li Lim‘s benchmark）之二

news2024/11/18 1:33:10

原文连接：知乎《使用Python调用Gurobi求解PDPTW问题（Li & Lim’s benchmark）》
分析文章：

文章目录

    • 修改
    • utlis.py
    • test.py
    • 运行DataPath="lc101.txt"

修改

以及修改公示约束（8）与代码不符合的问题。
约束(8)
添加depot的时间窗口约束,添加节点的时间窗口约束.这里的V包含depot和节点.depot的id为0.
∀ i ∈ V , ∀ k ∈ K \forall i \in V, \forall k \in K ∀i∈V,∀k∈K,
e i ≤ B i q ≤ l i e_i \leq B_i^q \leq l_i ei​≤Biq​≤li​

    # 约束（8）depot和customer的时间窗约束
    for k in Pro.Vehicles.keys():
        # 两个depot的时间窗约束
        model.addConstr(b[0, k] >= Pro.TimeWindow[0][0])
        model.addConstr(b[0, k] <= Pro.TimeWindow[0][1])
        model.addConstr(b[node_num - 1, k] >= Pro.TimeWindow[node_num - 1][0])
        model.addConstr(b[node_num - 1, k] <= Pro.TimeWindow[node_num - 1][1])
        model.addConstr(b[1, k] >= Pro.TimeWindow[1][0])
        #节点的时间窗口约束
        for i in range(node_num):
            model.addConstr(b[i,k] >= Pro.TimeWindow[i][0])
            model.addConstr(b[i,k] <= Pro.TimeWindow[i][1])

当depot不分为depot_start和depot_end的时候，修改为：

    for k in Pro.Vehicles.keys():
        for i in range(node_num):
            model.addConstr(b[i,k] >= Pro.TimeWindow[i][0])
            model.addConstr(b[i,k] <= Pro.TimeWindow[i][1])

现在代码可以分为两篇：utlis.py和test.py

utlis.py

  • class Pro():用于存储本问题的相关信息
  • def read_txt_data(DataPath,Pro)：读取车辆信息，并将结果放入Pro
  • def calculate_euclid_distance(x1, y1, x2, y2):定义了两个节点的距离公示
  • def Construct_DisTime_Matrix(Pro)：计算任意两个节点的距离矩阵（与车辆无关）和时间矩阵（含车辆）
  • def build_model(Pro)：建立PDPTW的问题模型

from gurobipy import *
import numpy as np
import pandas as pd
import math
import random
import time
class Pro():
    def __init__(self):
        self.Vehicles={} #用于存放车辆，适用于单depot的情况
        #self.Depots={}#用于存放depot,使用于多depot的情况。{d1:{车辆集1}，d2:{车辆集2}，...}
        self.Locations={}
        self.Demand={}
        self.TimeWindow={}
        self.ServiceTime={}
        self.Request={}
        self.node_num=None
        self.veh_num=None
        self.pair_num=None #成对约束的数量
        self.EarliestTime=None##depot的服务的最早时间
        self.LatestTime=None #depot的服务的最晚时间
        self.DistanceMatrix={}#用于存放节点(包括depot和需求节点)彼此之间的距离
        self.LongestDistance=None #最大节点间的距离
        self.TimeMatrix={}
def read_txt_data(DataPath,Pro):
    # 读取车辆信息u
    VehiclesInfo = pd.read_table(DataPath, nrows=1, names=['K', 'C', 'S'])

    for i in range(int(VehiclesInfo.iloc[0, 0])):
        Pro.Vehicles[i] = [VehiclesInfo.iloc[0, 1], VehiclesInfo.iloc[0, 2]]  # 键i=车辆的序号，值为[车辆容量、速度]

    Pro.veh_num=len(Pro.Vehicles)
    # 读取Depot和任务信息
    ColumnNames = ['TaskNo', 'X', 'Y', 'Demand', 'ET', 'LT', 'ST', 'PI', 'DI']
    # [任务标号,x坐标,y坐标,需求任务]
    TaskData = pd.read_table(DataPath, skiprows=[0], names=ColumnNames, index_col='TaskNo')

    # 提取Depot和取送货点（Customer）的位置坐标 Locations
    Pro.node_num = TaskData.shape[0]
    for i in range(Pro.node_num):
        if i not in Pro.Locations.keys():
            Pro.Locations[i] = [TaskData.iloc[i, 0], TaskData.iloc[i, 1]]  # 键为depot或客户编号，值为相应的坐标（x，y）

    # 提取Depot和取送货点的Demand
    for i in range(Pro.node_num):
        if i not in Pro.Demand.keys():
            Pro.Demand[i] = TaskData.iloc[i, 2]

    # 提取Depot和取送货点的最早和最晚取送货时间及时间窗

    Pro.EarliestTime = TaskData.sort_values(by='ET').iloc[0, 3]
    Pro.LatestTime = TaskData.sort_values(by='LT', ascending=False).iloc[0, 4]
    for i in range(Pro.node_num):
        if i not in Pro.TimeWindow.keys():
            Pro.TimeWindow[i] = [TaskData.iloc[i, 3], TaskData.iloc[i, 4]]
    # 提取Depot和取送货点的服务时间ServiceTime
    for i in range(Pro.node_num):
        if i not in Pro.ServiceTime.keys():
            Pro.ServiceTime[i] = TaskData.iloc[i, 5]

    # 提取运输Request
    # 对于取货任务，PICKUP索引为0，而同一行的DELIVERY索引给出相应送货任务的索引
    count = 0  # 记录运输需求的数量
    for i in range(1, Pro.node_num - 1):
        if TaskData.iloc[i, 6] == 0:
            Pro.Request[count] = [i, TaskData.iloc[i, 7]]  # 将取送货点组合在一起，键为count，值为[取货点，送货点]
            count += 1
    Pro.pair_num=count


def calculate_euclid_distance(x1, y1, x2, y2):
    """  计算Euclid距离.

    具体描述：计算两点(x1, y1), (x2, y2)之间的Euclid距离.
    """
    EuclidDistance = math.sqrt((x2-x1)**2 + (y2-y1)**2)
    return EuclidDistance

def Construct_DisTime_Matrix(Pro):
    #获得两个节点之间距离和时间距离
    Locations=Pro.Locations
    for i in Locations.keys():
        for j in Locations.keys():
            if i != j:
                Pro.DistanceMatrix[i, j] = calculate_euclid_distance(Locations[i][0], Locations[i][1],
                                                                    Locations[j][0], Locations[j][1])
    key = max(Pro.DistanceMatrix, key=Pro.DistanceMatrix.get)
    Pro.LongestDistance = Pro.DistanceMatrix[key]
    for k in range(Pro.veh_num):
        for i in Locations.keys():
            for j in Locations.keys():
                if i != j:
                    Pro.TimeMatrix[i, j, k] = Pro.DistanceMatrix[i, j] / Pro.Vehicles[k][1]



def build_model(Pro):
    # 建立pdptw问题的模型.
    # 创建模型
    model = Model()  # gurobipy中的Model()
    # 变量下标存放列表
    node_num=Pro.node_num
    ijk=[(i,j,k) for i in range(node_num) for j in range(node_num) if i!=j for k in range(Pro.veh_num)]
    ik=[(i,k) for i in range(node_num) for k in range(Pro.veh_num)]
    # 添加决策变量x_ijk，意为车辆k经过弧（i，j）
    # 添加状态变量q_ik,意为车辆k离开节点i的存储量
    # 添加状态变量b_ik,意为车辆k到达节点i的时间
    x = model.addVars(ijk, vtype=GRB.BINARY, name='x')  # 变量x_{ijk},GRB.BINARY表示{0,1}变量
    q = model.addVars(ik, vtype=GRB.INTEGER, name='q')  # 变量q_{ik},GRB.INTEGER为整数变量
    b = model.addVars(ik, vtype=GRB.CONTINUOUS, name='b')  # 变量b_{ik},GRB.CONTINUOUS为连续变量
    model.update()#将变量跟新加入，不添加该行的话，查看model的变量为空
    ## ================== VRPTW===================

    # 约束（1）every vertex has to be served exactly once，除了depot外，每个节点只被服务一次
    for i in range(1, node_num - 1):
        model.addConstr(x.sum(i, '*', '*') == 1,name="eq1-i%s"%i)  # 星号*的用法

    # 约束(2-3) guarantee that every vehicle starts at the depot and returns to the depot
    # at the end of its route. 每辆车必须从depot出发，最后回到depot
    # 约束(4) Flow conservation 流平衡约束
    for k in Pro.Vehicles.keys():
        model.addConstr(x.sum(0, '*', k) == 1,name="eq2-k%s"%k)  # 车辆k从depot出发
        model.addConstr(x.sum('*', node_num - 1, k) == 1,name="eq3-k%s"%k)  # 车辆k回到depot
        for i in range(1, node_num - 1):  # 车辆k在P和D的流平衡约束
            model.addConstr(x.sum(i, '*', k) == x.sum('*', i, k),name="eq4-k%s-i%s"%(k,i))

    # 约束 (5) Time variables are used to eliminate subtours,用时间变量来消除子回路约束
    # 需要用大M法来线性化该约束，M定义为 2*(LatestTime+LongestDistance)
    vars=model.getVars()
    for i,j,k in ijk:
        if i !=j:
            model.addConstr(b[j,k]+2*(1-x[i,j,k])*(Pro.LatestTime+Pro.LongestDistance) >=
            b[i,k]+Pro.ServiceTime[i]+Pro.TimeMatrix[i,j,k],name="eq5-k%s-i%s-j%s"%(k,i,j))

    # 约束(6-7) guarantee that a vehicle’s capacity is not exceeded throughout its tour，载货量平衡与车辆载量约束
    # 约束(6) 载货量平衡约束，需要用大M法来线性化该约束，M定义为 100*车辆最大载量

    for i,j,k in ijk:
        if i!=j:
            model.addConstr(q[j,k]+(1-x[i,j,k])*(100*Pro.Vehicles[k][0])>=q[i,k]+Pro.Demand[j],name="eq6-k%s-i%s-j%s"%(k,i,j))

    # 约束（7）车辆载量约束
    for i,k in ik:
        model.addConstr(q[i,k] >=0, name="eq7.1-k%s-i%s"%(k,i))
        model.addConstr(q[i,k] >=Pro.Demand[i],name="eq7.2-k%s-i%s"%(k,i))
        model.addConstr(q[i,k] <= Pro.Vehicles[k][0],name="eq7.3-k%s-i%s"%(k,i))
        model.addConstr(q[i,k] <=Pro.Vehicles[k][0]+Pro.Demand[i],name="eq7.4-k%s-i%s"%(k,i))

    # 约束（8）depot和customer的时间窗约束
    for k in Pro.Vehicles.keys():
        # 两个depot的时间窗约束
        model.addConstr(b[0, k] >= Pro.TimeWindow[0][0])
        model.addConstr(b[0, k] <= Pro.TimeWindow[0][1])
        model.addConstr(b[node_num - 1, k] >= Pro.TimeWindow[node_num - 1][0])
        model.addConstr(b[node_num - 1, k] <= Pro.TimeWindow[node_num - 1][1])
        #节点的时间窗口约束
        for i in range(node_num):
            model.addConstr(b[i,k] >= Pro.TimeWindow[i][0])
            model.addConstr(b[i,k] <= Pro.TimeWindow[i][1])
    # 旧代码的写法
    # for k in Pro.Vehicles.keys():
    #     # 两个depot的时间窗约束
    #
    #     model.addConstr(b[0, k] >= Pro.TimeWindow[0][0])
    #     model.addConstr(b[0, k] <= Pro.TimeWindow[0][1])
    #     model.addConstr(b[node_num - 1, k] >= Pro.TimeWindow[node_num - 1][0])
    #     model.addConstr(b[node_num - 1, k] <= Pro.TimeWindow[node_num - 1][1])
    #     Request=Pro.Request
    #     for r in range(Pro.pair_num):
    #         # 运输请求i两个节点的左时间窗
    #         model.addConstr(b[Request[r][0], k] >= Pro.TimeWindow[Request[r][0]][0])
    #         model.addConstr(b[Request[r][1], k] >= Pro.TimeWindow[Request[r][1]][0])
    #         # 运输请求i两个节点的右时间窗
    #         model.addConstr(b[Request[r][0], k] <= Pro.TimeWindow[Request[r][0]][1])
    #         model.addConstr(b[Request[r][1], k] <= Pro.TimeWindow[Request[r][1]][1])

    ## ================== PDPTW===================

    # 约束（9）both origin and destination of a request must be served by the same vehicle
    # 保证取货后要有对应的送货，取货和送货由同一辆车完成
    for p in range(Pro.pair_num):
        for k in Pro.Vehicles.keys():
            model.addConstr(x.sum(Pro.Request[p][0], '*', k) == x.sum('*', Pro.Request[p][1], k),name="eq9-p%s"%p)

    # 约束 (10) delivery can only occur after pickup,先取后送货约束
    for p in range(Pro.pair_num):
        for k in Pro.Vehicles.keys():
            model.addConstr(b[Pro.Request[p][0], k] <= b[Pro.Request[p][1], k],name="eq10-p%s-k%s"%(p,k))

    ## 设置目标函数
    # 目标函数（3）:最小化车辆总的行驶距离
    DistanceCost = 0
    for k in Pro.Vehicles.keys():
        for i in range(node_num):
            for j in range(node_num):
                if i != j:
                    DistanceCost += (Pro.DistanceMatrix[i, j] * x[i, j, k])
    model.setObjective(DistanceCost, GRB.MINIMIZE)
    model.update()

    model.__data = x, b, q

    return model

test.py

from gurobipy import *
import time
from utlis import Pro, read_txt_data, Construct_DisTime_Matrix, build_model

Pro=Pro()
start = time.time()
# DataPath="lc101.txt"
DataPath="smallcase.txt"
read_txt_data(DataPath,Pro)
Construct_DisTime_Matrix(Pro)

model=build_model(Pro)
model.params.TimeLimit = 1000    # 设定模型求解时间
model.write('PDPTW_%s.lp' % DataPath)
model.write('PDPTW_%s.mps' % DataPath)
model.setParam(GRB.Param.LogFile, 'PDPTW_%s.log' % DataPath)
model.optimize()
x,b,q = model.__data

end = time.time()
print('程序运行时间：')
print(end-start)

程序运行时间：
0.13767194747924805
查看结果

Optimize a model with 2588 rows, 1100 columns and 9060 nonzeros
Variable types: 100 continuous, 1000 integer (900 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+04]
Objective range [1e+01, 4e+01]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+04]

Presolve removed 740 rows and 50 columns
Presolve time: 0.03s
Presolved: 1848 rows, 1050 columns, 11628 nonzeros
Variable types: 100 continuous, 950 integer (850 binary)

Root relaxation: objective 8.000000e+01, 60 iterations, 0.00 seconds (0.00 work units)

Cutting planes:
Learned: 1
Gomory: 1
Implied bound: 39
MIR: 13
StrongCG: 3
RLT: 5
Relax-and-lift: 3

Explored 68 nodes (2136 simplex iterations) in 0.60 seconds (0.36 work units)
Thread count was 8 (of 8 available processors)

输出结果

# 输出方式2
for k in Pro.Vehicles.keys():
    for i in range(Pro.node_num):
        for j in range(Pro.node_num):
            if i != j:
                if (x[i,j,k].X- 0.5 > 0):
                    print('tour for vehicle %s:' % k)
                    print('%s-->%s' % (i,j))

out:
tour for vehicle 0:
0–>9
tour for vehicle 1:
0–>9
tour for vehicle 2:
0–>9
tour for vehicle 3:
0–>9
tour for vehicle 4:
0–>9
tour for vehicle 5:
0–>9
tour for vehicle 6:
0–>9
tour for vehicle 7:
0–>9
tour for vehicle 8:
0–>9
tour for vehicle 9:
0–>1
tour for vehicle 9:
1–>2
tour for vehicle 9:
2–>3
tour for vehicle 9:
3–>4
tour for vehicle 9:
4–>5
tour for vehicle 9:
5–>6
tour for vehicle 9:
6–>7
tour for vehicle 9:
7–>8
tour for vehicle 9:
8–>9

运行DataPath=“lc101.txt”

运行该程序，会出现模型不可解的现象。运行下面的代码。检查哪个约束条件出了问题。

if model.status == GRB.Status.INFEASIBLE:
        print('Optimization was stopped with status %d' % model.status)
        # do IIS, find infeasible constraints
        model.computeIIS()
        for c in model.getConstrs():
            if c.IISConstr:
                print('%s' % c.constrName)

out:

eq1-i97
eq3-k9
eq3-k13
eq9-p50-k9
eq9-p50-k13

检查：
公式1
∀ i ∈ P ∪ D = { 1 , 2 , ⋯   , n , n + 1 , ⋯   , n + n } \forall i \in P\cup D=\{1,2,\cdots,n,n+1,\cdots,n+n\} ∀i∈P∪D={1,2,⋯,n,n+1,⋯,n+n}
∑ k ∈ K ∑ j : ( i , j ) ∈ A x i j k = 1 (1) \sum_{k\in K}\sum_{j:(i,j)\in A}x^k_{ij}=1 \tag{1} k∈K∑​j:(i,j)∈A∑​xijk​=1(1)
对于i=97的时候。
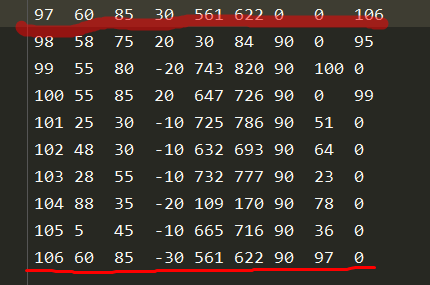
在这里插入图片描述
发现，与“smallcase.txt”最后位置少一行depot_end的一行数据.所以，导致在运行过程中，删除了97的对应节</f点。
公式3
∀ k ∈ K \forall k \in K ∀k∈K
∑ j : ( 0 , j ) ∈ A x 0 , j k = 1 \sum_{j:(0,j)\in A}x_{0,j}^k=1 j:(0,j)∈A∑​x0,jk​=1
∑ i : ( i , n + n ~ + 1 ) ∈ A x i , n + n ~ + 1 k = 1 \sum_{i:(i,n+\tilde{n}+1)\in A} x^k_{i, n+\tilde{n}+1}=1 i:(i,n+n~+1)∈A∑​xi,n+n~+1k​=1

for k in Vehicles.keys():
    model.addConstr(x.sum(0,'*',k) == 1)       # 车辆k从depot出发
    model.addConstr(x.sum('*',nrows-1,k) == 1)       # 车辆k回到depot

表示：对于车辆k来说，仅有一次从depot出发，并仅有一次返回depot.这里的nrows-1值得使106行。而不是depot行。

约束(9)
弧(i,j)必须由同一辆车经过(先取货再送货).假设这些弧集为特定的集合 A ~ \tilde{A} A~
∀ k ∈ K \forall k \in K ∀k∈K, ∀ ( i , j ) ∈ A ~ \forall (i,j)\in \tilde{A} ∀(i,j)∈A~
∑ j : ( i , j ) ∈ A ~ x i j k = ∑ i : ( i , j ) ∈ A ~ x i j k \sum_{j:(i,j)\in \tilde{A}}x_{ij}^k=\sum_{i:(i,j)\in \tilde{A}}x_{ij}^k j:(i,j)∈A~∑​xijk​=i:(i,j)∈A~∑​xijk​

    for r in range(len(Request)):
        for k in range(len(Vehicles)):
            model.addConstr(x.sum(Request[r][0],'*',k)==x.sum('*',Request[r][1],k))

Request = {…, 48: [92, 93], 49: [96, 94], 50: [97, 106], 51: [98, 95], 52: [100, 99]}
检查Request中的key=50的值为：50 : [97, 106]

经查验，就是因为两个文件中depot的数量不同引起的。在”smallcase.txt"中将depot划分为depot_start和depot_end.而在“lc101.txt”中仅仅有一个depot.

要检查的地方有

  • 数据读取的方式
#def read_txt_data(DataPath,Pro)
    count = 0  # 记录运输需求的数量
    for i in range(1, Pro.node_num ):
        if TaskData.iloc[i, 6] == 0:
            Pro.Request[count] = [i, TaskData.iloc[i, 7]]  # 将取送货点组合在一起，键为count，值为[取货点，送货点]
            count += 1
    Pro.pair_num=count
  • 公式3：关于depot的索引修改
# def build_model(Pro):
## 约束3中，返回depot的数字id为0，而不死node_num-1
    for k in Pro.Vehicles.keys():
        model.addConstr(x.sum(0, '*', k) == 1,name="eq2-k%s"%k)  # 车辆k从depot出发
        # model.addConstr(x.sum('*', node_num - 1, k) == 1,name="eq3-k%s"%k)
        model.addConstr(x.sum('*', 0, k) == 1,name="eq3-k%s"%k)# 车辆k回到depot ###公式3
        for i in range(1, node_num - 1):  # 车辆k在P和D的流平衡约束
            model.addConstr(x.sum(i, '*', k) == x.sum('*', i, k),name="eq4-k%s-i%s"%(k,i))

修正文件
但是最简单的方法，还是在“lc101.txt"最后一行加一个depot_end的信息。如下所示。
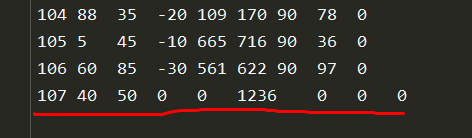
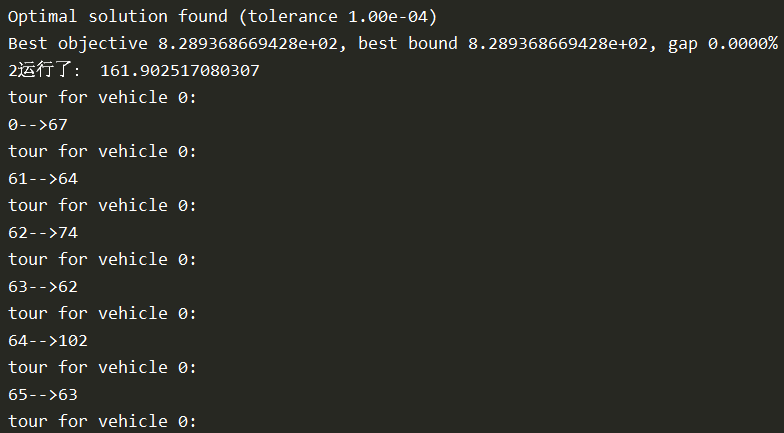
在这里插入图片描述
输出结果：
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/133637.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【QT开发笔记-基础篇】| 第五章 绘图QPainter | 5.13 抗锯齿

【QT开发笔记-基础篇】| 第五章 绘图QPainter | 5.13 抗锯齿

本节对应的视频讲解&#xff1a;B_站_视_频 https://www.bilibili.com/video/BV1YP4y1B7Ex 本节讲解抗锯齿效果 前面实现的效果中&#xff0c;仔细观看能看到明显的锯齿的效果&#xff0c;如下&#xff1a; 此时&#xff0c;可以增加抗锯齿的效果。 1. 关联信号槽 首先&…
阅读更多...
22年12月日常实习总结

22年12月日常实习总结

12月结束了&#xff0c;8月末开始准备的日常实习也算是告一段落了 准备了2个多月&#xff0c;面试了一个月&#xff0c;也拿了一些offer 算是小有感触&#xff0c;遂写下此文&#xff0c;供还在准备或者要准备日常实习的同学参考。 个人背景及投递的日常实录在这篇文章里 24…
阅读更多...
RegNet——颠覆常规神经网络认知的卷积神经网络（网络结构详解+详细注释代码+核心思想讲解）——pytorch实现

RegNet——颠覆常规神经网络认知的卷积神经网络（网络结构详解+详细注释代码+核心思想讲解）——pytorch实现

RegNet的博客的准备我可谓是话费了很多的时间&#xff0c;参考了诸多大佬的资料&#xff0c;主要是网上对于这个网络的讲解有点少&#xff0c;毕竟这个网络很新。网上可以参考的资料太少&#xff0c;耗费了相当多的时间&#xff0c;不过一切都是值得的&#xff0c;毕竟学完之后…
阅读更多...
第二证券|下周解禁市值超980亿元，多家机构参与解禁股评级

第二证券|下周解禁市值超980亿元，多家机构参与解禁股评级

宁德年代迎来431.8亿元解禁。 下周A股解禁市值超980亿元 证券时报数据宝统计&#xff0c;1月3日至6日&#xff0c;A股商场将有53家上市公司迎来限售股解禁。以个股最新价计算&#xff0c;53股解禁市值合计981.68亿元。 从解禁规模来看&#xff0c;宁德年代和中国移动居前&…
阅读更多...
4.搭建配置中心-使用SpringCloud Alibaba-Nacos

4.搭建配置中心-使用SpringCloud Alibaba-Nacos

naocs除了做服务注册、发现&#xff0c;还可以做为配置中心&#xff0c;使用分以下几步 1.pom引入nacos-config依赖 <dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-starter-alibaba-nacos-config</artifactId> &…
阅读更多...
python中的多态和抽象类接口

python中的多态和抽象类接口

目录 一.多态 抽象类&#xff08;接口&#xff09; 小结 一.多态 多态&#xff0c;指的是:多种状态&#xff0c;即完成某个行为时&#xff0c;使用不同的对象会得到不同的状态。 同样的行为&#xff08;函数&#xff09;&#xff0c;传入不同的对象得到不同的状态 演示 cl…
阅读更多...
降维算法-sklearn

降维算法-sklearn

1.概述 维度&#xff1a; 对于数组和series&#xff0c;维度就是功能shape返回的结果&#xff0c;shape中返回了几个数字&#xff0c;就是几个维度。降维算法中的”降维“&#xff0c;指的是降低特征矩阵中特征的数量。降维的目的是为了让算法运算更快&#xff0c;效果更好&am…
阅读更多...
LabVIEW​​开关模块与万用表DMM扫描模式

LabVIEW​​开关模块与万用表DMM扫描模式

LabVIEW​​开关模块与万用表DMM扫描模式 在同步扫描模式下(Synchronous scanning)&#xff0c;扫描列表里面的每一条目都会在开关模块收到一个来自多功能数字万用表(DMM)的数字脉冲(触发输入)后执行.而DMM被编程设置为以一个固定的时间间隔去测量以及在每次测量完产生一个数字…
阅读更多...
机器学习--数据清理、数据变换、特征工程

机器学习--数据清理、数据变换、特征工程

目录 一、数据清理 二、数据变换 三、特征工程 四、总结 一、数据清理 数据清理是提升数据的质量的一种方式。 数据不干净&#xff08;噪声多&#xff09;&#xff1f; 需要做数据的清理&#xff0c;将错误的信息纠正过来&#xff1b; 数据比较干净&#xff08;数据不是…
阅读更多...
STM32 TIM PWM初阶操作：非互补PWM输出

STM32 TIM PWM初阶操作：非互补PWM输出

STM32 TIM PWM初阶操作详解&#xff1a;非互补PWM输出 STM32 TIM可以输出管脚PWM信号适合多种场景使用&#xff0c;功能包括单线/非互补PWM输出&#xff0c;双线/互补PWM输出&#xff0c;以及死区时间和刹车控制等。 实际上&#xff0c;因为早期IP Core的缺陷&#xff0c;早期…
阅读更多...
Android多线程编程

Android多线程编程

二.Android多线程编程 1.线程的相关概念 1&#xff09;相关概念&#xff1a; 程序&#xff1a;为了完成特定任务&#xff0c;用某种语言编写的一组指令集合(一组静态代码)进程&#xff1a;运行中的程序&#xff0c;系统调度与资源分配的一个独立单位&#xff0c;操作系统会 为…
阅读更多...
leetcode 207. 课程表——java题解

leetcode 207. 课程表——java题解

题目所属分类 类似有向图的拓扑排序 入度为0就是起点 因为是要按照先后顺序的&#xff0c;所以是就是有向图 原题链接 你这个学期必须选修 numCourses 门课程&#xff0c;记为 0 到 numCourses - 1 。 在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites …
阅读更多...
Jetpack Compose中的Accompanist

Jetpack Compose中的Accompanist

accompanist是Jetpack Compose官方提供的一个辅助工具库&#xff0c;以提供那些在Jetpack Compose sdk中目前还没有的功能API。 权限 依赖配置&#xff1a; repositories {mavenCentral() }dependencies {implementation "com.google.accompanist:accompanist-permissi…
阅读更多...
阳后买不到温度计 那么自己diy！（已开源）

阳后买不到温度计 那么自己diy！（已开源）

这里写目录标题一 说明二 成品效果三 硬件材料四 硬件连接五 软件六 3D外盒模型一 说明 前段时间放开疫情后&#xff0c;身边人基本都阳了&#xff0c;自己也不出所料阳了&#xff0c;然后去药店买温度计&#xff0c;发现买不到&#xff0c;网上的买了也不发货&#xff0c;但是…
阅读更多...
7.JS笔记-数组

7.JS笔记-数组

1.数组的概念 使用数组Array可以把一组相关的数据存放在一起&#xff0c;并提供方便的获取方式。 数组是一组数据的集合&#xff0c;其中的每个数据被称作是元素&#xff0c;在数组中可以存放任意类型的元素。数组是一种将数据存储在单个变量名下的方式 2.创建数组 利用new关…
阅读更多...
【Linux】Linux进程的理解 --- 进程状态、优先级、切换…

【Linux】Linux进程的理解 --- 进程状态、优先级、切换…

如果不改变自己&#xff0c;就别把跨年搞的和分水岭一样&#xff0c;记住你今年是什么吊样&#xff0c;明年就还会是什么吊样&#xff01;&#xff01;&#xff01; 文章目录一、冯诺依曼体系结构&#xff08;硬件&#xff09;二、操作系统&#xff08;软件&#xff09;1.操作…
阅读更多...
git笔记2：Git基本理论，项目创建及克隆

git笔记2：Git基本理论，项目创建及克隆

目录 一、工作区域 二、工作流程 三、本地仓库搭建 1、创建全新的仓库 2、克隆远程仓库 一、工作区域 Git本地有三个工作区域&#xff1a; 工作目录&#xff08;Working Directory&#xff09;&#xff1a;平时存放代码的地方暂存区&#xff08;Stage/Index&#xff09;&a…
阅读更多...
sec6-可派生类型和抽象类型

sec6-可派生类型和抽象类型

可派生类型 有两种类型&#xff0c;final类型和derivable类型。final类型没有任何子对象。derivable有子对象。 这两个对象之间的主要区别是它们的类。final类型对象没有自己的类区域。类的唯一成员是它的父类。 派生对象在类中有自己的区域。该类对其子类开放。 G_DECLARE…
阅读更多...
【python系列】第三章 基本数据类型

【python系列】第三章 基本数据类型

*该系列内容来自于&#xff1a;中国大学MOOC&#xff08;幕客&#xff09;-python语言程序设计 ​​​​​​Python语言程序设计_北京理工大学_中国大学MOOC(慕课) 第三章 基本数据类型 方法论&#xff1a;Python语言数字及字符串类型 实践能力&#xff1a;初步学会编程进行…
阅读更多...
236. 二叉树的最近公共祖先 - 力扣[LeetCode]

236. 二叉树的最近公共祖先 - 力扣[LeetCode]

目录 如果二叉树是二叉搜索树&#xff1a; 如果是普通的二叉树 【方法一】子树判断法 【方法二】路径确定 【方法三】递归 面对此类型的公共祖先问题&#xff0c;可以分为以下几类情况讨论 如果二叉树是二叉搜索树&#xff1a; a. 如果树是空&#xff0c;直接返回nullpt…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023