*该系列内容来自于：中国大学MOOC（幕客）-python语言程序设计

​​​​​​Python语言程序设计_北京理工大学_中国大学MOOC(慕课)
第三章  基本数据类型

方法论：Python语言数字及字符串类型
实践能力：初步学会编程进行字符类操作

3.1  数字类型及操作
3.1.1  整数：
1、pow(x,y)   x的y次方
2、4种进制表示形式
十进制：10,20
二进制：0B 0b
八进制：0O  0o
十六进制：0X  0x

3.1.2  浮点数——实数
1、浮点数间运算确定不确定尾数，不是bug
>>>>>0.1+0.2（二进制表示小数，可以无限接近，但不完全相同）
0.300000000000004（不确定尾数）
2、>>>>>0.1+0.2==0.3   FALSE
     >>>>>round(0.1+0.2,1) ==0.3   TRUE
 round(x,d)：对x四舍五入，d是小数截取位数
 浮点数间运算及比较用round()函数辅助

3、科学计数法
使用E或e作为幂的符号，以10为基数
4.3e-3    0.0043


3.1.3  负数——复试
1、x的平方=-1
定义 j=根号下（-1）
a+bj被称为复数，a是实部，b是虚部

2、复数实例
z=1.23e-4+5.6e+89j
z.real获得实部
z.imag获得虚部


3.1.4  数值运算操作符
1、基本操作符
+    -    *    /（10/3结果3.33333333 浮点类型）    //（整数除 10//3结果3）
+x（x本身）   -y（y负值）   x%y（余数   模运算  10%3结果1）   x**y（幂运算  x的y次幂）（当y是小数时，开方运算  10**0.5结果 根号10）

2、二元操作符
x op=y
x=x op y    op是二元操作符
  x+=y     x-=y     x*=y     x/=y
  x//=y     x%=y     x**=y
例 x=3.1415   x**=3     与x=x**3等价

3、类型间可进行混合运算，生成结果为“最宽”类型
整数->浮点数->复数
123+4.0=127.0（整数+浮点数=浮点数）

3.1.5  数值运算函数
1、基本函数
abs(x)    绝对值，x的绝对值                          abs(-10.01)结果为 10.01
divmod(x,y)   商余，（x//y,x%y）,同时输出商和余数                    divmod(10,3)结果为（3,1）
pow(x,y,[z])  幂余，（x**y）%z，[z]表示参数z可以省略                      pow(3,pow(3,99),100000) 结果为 4587
round(x,[d])  四舍五入，d是保留小数位数，默认值为0                     round(-10.123,2)结果为-10.12
max(x1,x2,x3,...)  返回最大值
min(x1,x2,x3,...)  返回最小值

2、数字类型转换函数
int(x)   将x变成整数，舍弃小数部分
float(x)   将x变成浮点数，增加小数部分
complex(x)   将x变成复数，增加虚数部分



3.2 实例3：天天向上的力量
 基本问题：持续的价值
一年365天，每天进步1%，累计进步多少？
     1.01的365次方
一年365天，每天退步1%，累计剩下多少？
     0.99的365次方

-“三天打鱼两天晒网”
-“双休日又不退步”

问题1:千分之一的力量
#DayDayUpQ1.py
dayup=pow(1.001,365)
daydown=pow(0.999,365)
print("向上:{:.2f},向下:{:.2f}".format(dayup,daydown))

向上:1.44,向下:0.69
问题二：千分之五和百分之一的力量
#DayDayUpQ2.py
dayfactor=0.005
dayup=pow(1+dayfactor,365)
daydown=pow(1-dayfactor,365)
print("向上:{:.2f},向下:{:.2f}".format(dayup,daydown))

向上:6.17,向下:0.16
向上:37.78,向下:0.03
使用变量的好处：一处修改即可


问题三：工作日的力量
一年365天，一周5个工作日，每天进步1%
一年365天，一周2个休息日，每天退步1%
这种工作日的力量，如何？

#DayDayUpQ3.py
dayup=1.0
dayfactor=0.01
for i in range(365):
    if i%7 in [6,0]:
        dayup=dayup*(1-dayfactor)
    else:
        dayup=dayup*(1+dayfactor)
print("工作日的力量：{:.2f}".format(dayup))

工作日的力量：4.63
从数学思维到计算思维

问题四：工作日的努力
工作日模式要努力到什么水平，才能与每天努力1%一样？
for .. in ..（计算思维）  ——  def .. while..（笨办法试错）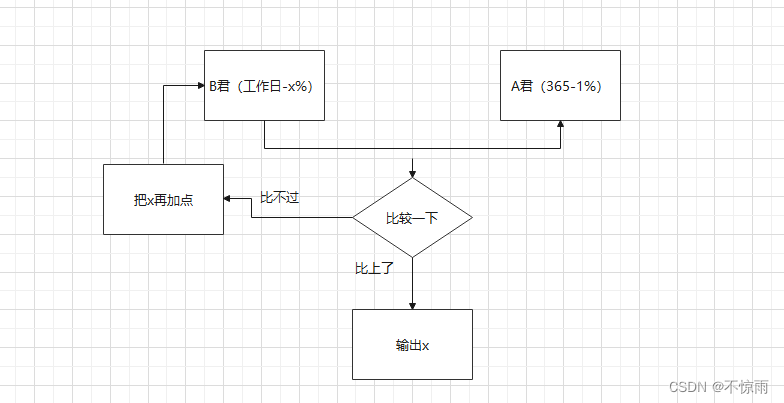


def dayUP(df):
    dayup=1
    for i in range (365):
        if i%7 in [6,0]:
            dayup =dayup*(1-0.01)
        else:
            dayup =dayup*(1+df)
    return dayup
dayfactor=0.01
while dayUP(dayfactor)<37.78:
    dayfactor+=0.001
print("工作日的努力参数是：{:.3f}".format(dayfactor))

工作日的努力参数是：0.019
根据df参数计算工作日力量的函数
参数不同，这段代码可共用
def保留字用于定义函数

while保留字判断条件是否成立
条件成立时循环执行

grit：坚毅，对长期目标的持续激情及持久耐力

举一反三：
计算思维=抽象+自动化


3.3  字符串类型及操作
3.3.1  字符串类型的表示
1、字符串——字符有序序列，可进行索引
2、2类4种表示方式
一对单引号/双引号——单行字符串
一对三单引号/三双引号——多行字符串

'这里有个双引号（"）'或者"这里有个单引号（'）"
'"这里既有单引号（'）又有双引号（"）"'
3、字符串的序号：正向递增序号和反向递减序号
索引[]    切片[]
切片高级使用：[M:N:K]  根据步长对字符串切片
[::-1]  逆序表示
4、特殊字符
转义符 \  特定字符的本意  
"这里有个双引号（\"）"    结果为     这里有个双引号（"）



3.3.2  字符串操作符
1、


2、






3.3.3  字符串处理函数
1、




2、Unicode编码


3、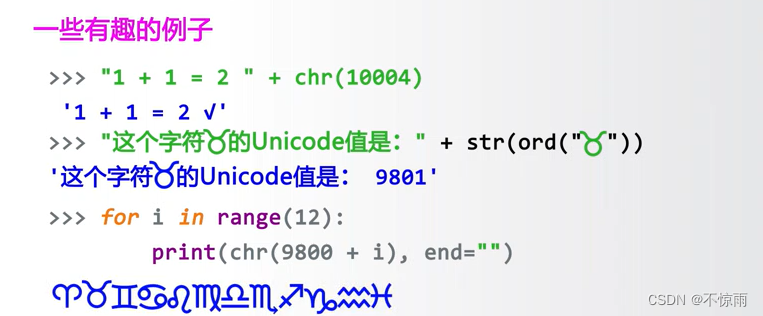


3.3.4  字符串处理方法
1、


面向对象——方法
2、






3.3.5  字符串类型的格式化
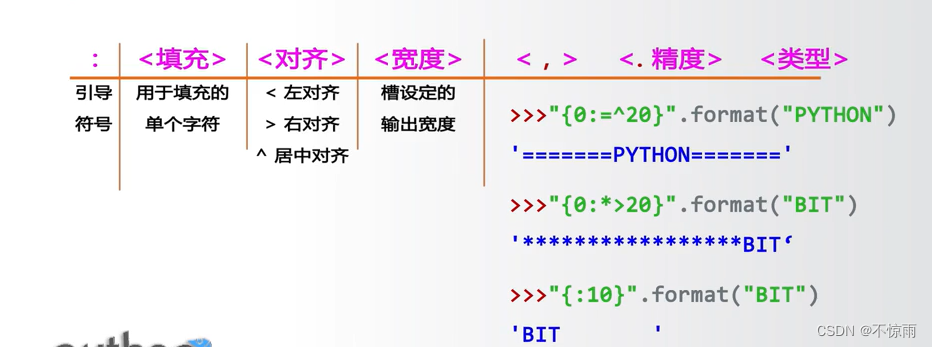
1、


2、槽——{}——字符串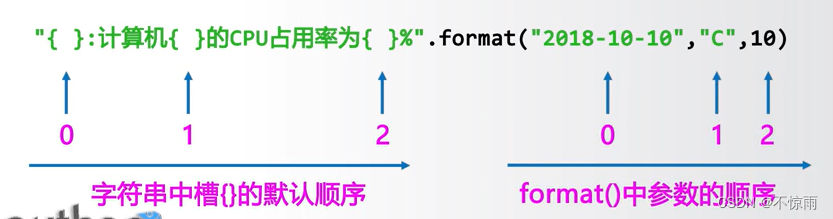




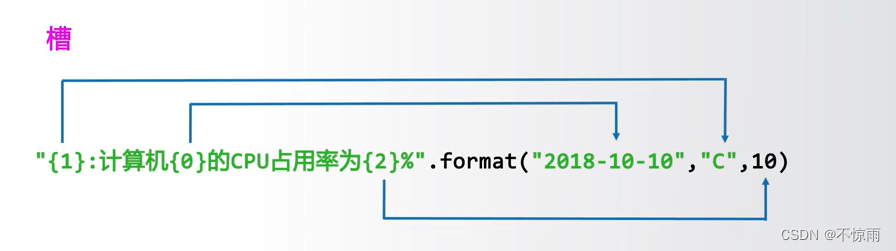
3、














3.4  模块2：time 库的使用
3.4.1  time库基本介绍
1、


2、




3.4.2  时间获取
1、





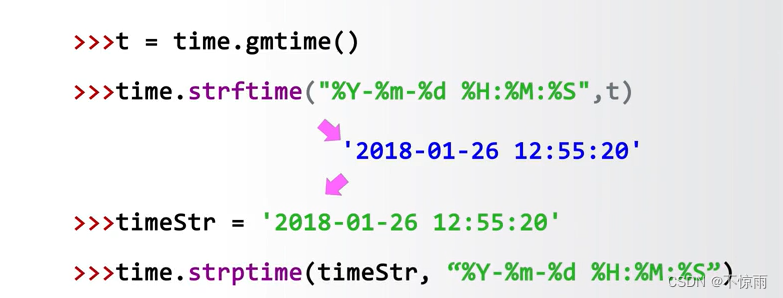
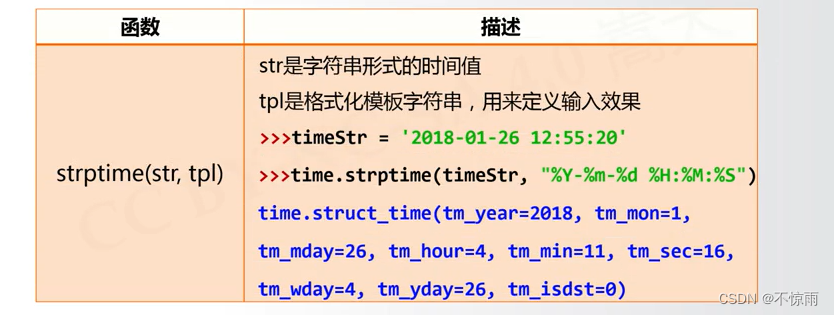
3.4.3  时间格式化
1、


2、












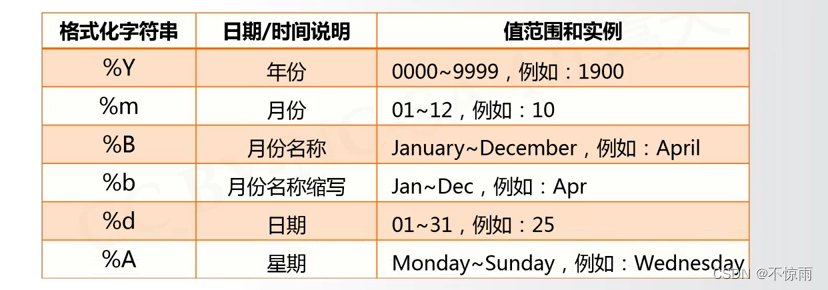
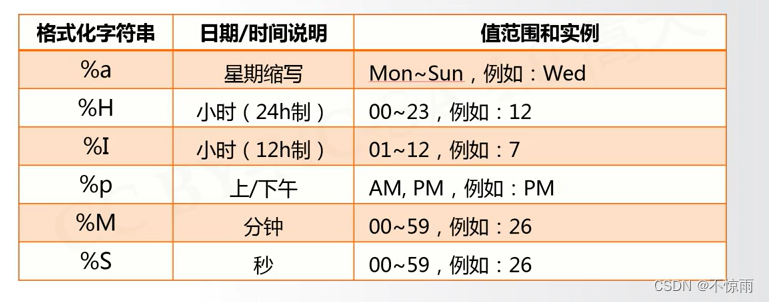
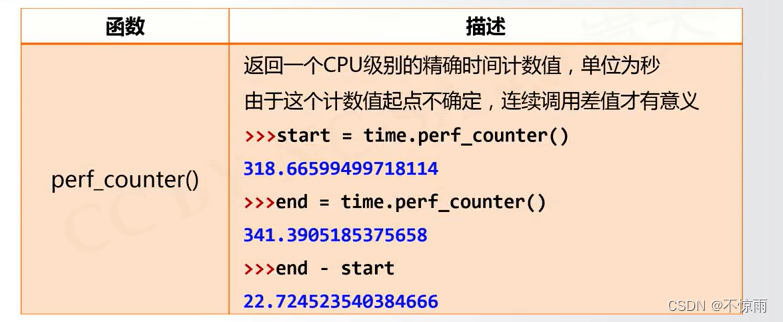
3.4.4  程序计时应用







3.5  实例4：文本进度条
3.5.1  “文本进度条”问题分析








3.5.2  “文本进度条”简单的开始




3.5.3  “文本进度条”单行动态刷新







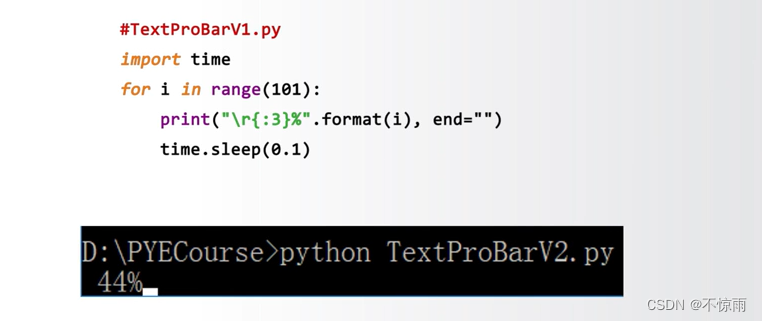
3.5.4  “文本进度条”实例完整效果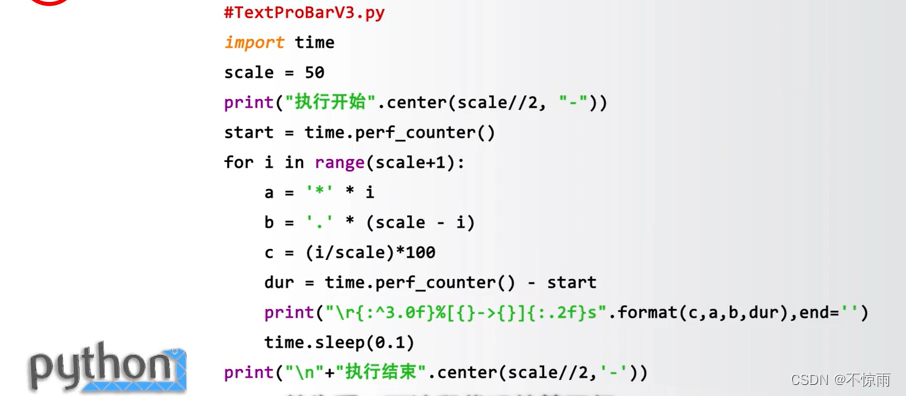






3.5.5  “文本进度条”举一反三






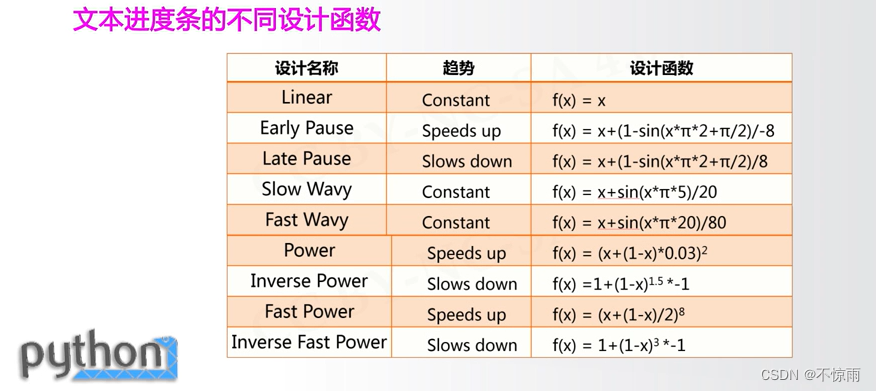
惊喜感