如果二叉树是二叉搜索树：

a. 如果树是空，直接返回nullptr，没有最近公共祖先节点

b. 如果两个节点中有一个是根节点，最近公共祖先一定是根节点

c. 如果两个节点一个比根节点大，一个比根节点小，最近公共祖先一定是根节点

d. 如果两个节点都比根节点小，递归到根的左子树中查找

e. 如果两个节点都比根节点大，递归到根的右子树中查找

二叉搜索树的最近公共祖先_牛客题霸_牛客网

int lowestCommonAncestor(struct TreeNode* root, int p, int q ) {
    // write code here
    if(NULL == root)
    return -1;
    if(p<=root->val && q>=root->val || p>=root->val && q<=root->val)
    return root->val;
    else if(p<=root->val && q<=root->val)
    return lowestCommonAncestor(root->left, p, q);
    else
    return lowestCommonAncestor(root->right, p, q);
}

如果是普通的二叉树

力扣https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/

236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

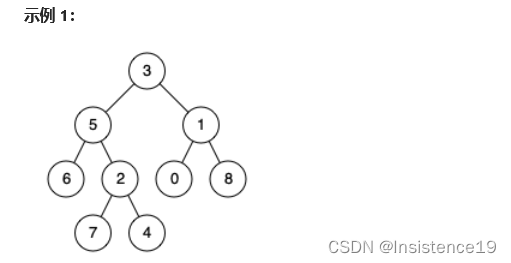
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

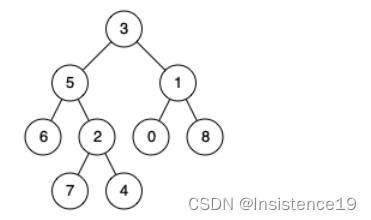
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

    树中节点数目在范围 [2, 105] 内。
    -109 <= Node.val <= 109
    所有 Node.val 互不相同。
    p != q
    p 和 q 均存在于给定的二叉树中。

【方法一】子树判断法

解题思路：

要求：找到俩个结点的最近公共祖先，并返回该祖先结点

参数：一个具有二叉树序列的根节点、第一个查找值结点指针、第二个查找值结点指针。

想到可以通过判断结点为另一个结点子树的特性，如果subroot1为root的子树结点，那么该root节点即为该root的祖先，如果subroot2也同时为root的子树，那么该root即为其共同的公共祖先。

题目又要求找最近的公共祖先，那么只需要初始化一个指针，找到俩个结点的第一个公共祖先，并不断维护这个指针，使其一直指向俩结点的公共祖先。

    void dfs(TreeNode* root, TreeNode* p, TreeNode* q)
    {
        if(root==NULL)
        return;
        if(Issubtree(root, p) && Issubtree(root, q))
            res = root;
        dfs(root->left, p, q);
        dfs(root->right, p, q);
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        dfs(root,p,q);
        return res;

如果root到了NULL的位置直接返回，如果p q同时为root的子树，那么更新res，使其指向该root结点，并持续不断进行遍历二叉树。

接着给出子树的函数

子树不为空条件下可以省略下方俩步判断

    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        // if(root==NULL && subRoot==NULL)
        // return true;
        if(root==NULL && subRoot!=NULL)
        return false;
        // if(root!=NULL && subRoot==NULL)
        // return false;
        if(isSameTree(root,subRoot))
        return true;
        return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
    }

接着给出俩树相同判断

    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(!p && !q)
        return true;
        if(!q || !p)
        return false;
        if(p->val == q->val)
            return isSameTree(p->left,q->left) && 
                    isSameTree(p->right, q->right);
        else
            return false;
    }

【方法二】路径确定

如果能够知道节点到根的路径，问题就解决了获取节点pNode的路径，因为
公共祖先从下往上找，因此将路径中的节点保存在栈中
a. 如果是空树，直接返回
b. 将根节点入栈，如果根节点和pNode是同一个节点，该节点到根的路径找到，否则：
c. 递归在根节点的左子树中查找，如果找到，返回
d. 如果在根节点的左子树中未找到，递归到根节点的右子树中找
e. 如果右子树中没有找到，说明root一定不再路径中

1. 在二叉树中获取两个节点的路径

2. 如果两个路径中节点个数不一样，节点多的出栈，直到两个栈中元素相等

相等时：再比较两个栈顶是不是同一个节点，如果是，最近公共祖先找到，如果不是，两个栈同时进行出栈，继续比较，直到找到为止

class Solution {
public:
	bool GetNodePath(TreeNode* pRoot, TreeNode* pNode, stack<TreeNode*>& path)
	{
		// 空树：直接返回
		if (nullptr == pRoot)
			return false;
		// 先将根节点放在路径中
		path.push(pRoot);
		// 如果根节点和pNode相等，路径找到
		if (pNode == pRoot)
			return true;
		// 如果根节点和pNode不相等，先递归在左子树中找，找到则退出
		bool isPath = false;
		if (isPath = GetNodePath(pRoot->left, pNode, path))
			return true;
		// 未找到时，再到根节点的右子树中找
		if (isPath = GetNodePath(pRoot->right, pNode, path))
			return true;
		// 如果左右子树中都没有找到，说明根节点不在路径中
		path.pop();
		return false;
	}
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		// 如果是空树，不存在最近公共祖先节点
		if (nullptr == root)
			return nullptr;
		// 获取两个节点在二叉树中的路径，并保存在栈中
		stack<TreeNode*> pPath;
		stack<TreeNode*> qPath;
		GetNodePath(root, p, pPath);
		GetNodePath(root, q, qPath);
		// 找最近公共祖先
		size_t pSize = pPath.size();
		size_t qSize = qPath.size();
		TreeNode* pCommonAncestor = nullptr;
		while (pSize && qSize)
		{
			// 如果两个栈中元素不相等，长的先出栈，直到两个栈中元素相等
			if (pSize > qSize)
			{
				pPath.pop();
				pSize--;
			}
			else if (pSize < qSize)
			{
				qPath.pop();
				qSize--;
			}
			else
			{
				// 如果栈顶元素相等，即为最近公共祖先
				// 否则：两个栈同时出栈
				if (pPath.top() == qPath.top())
				{
					pCommonAncestor = pPath.top();
					break;
				}
				else
				{
					pPath.pop();
					qPath.pop();
					pSize--;
					qSize--;
				}
			}
		}
		return pCommonAncestor;
	}
};

【方法三】递归

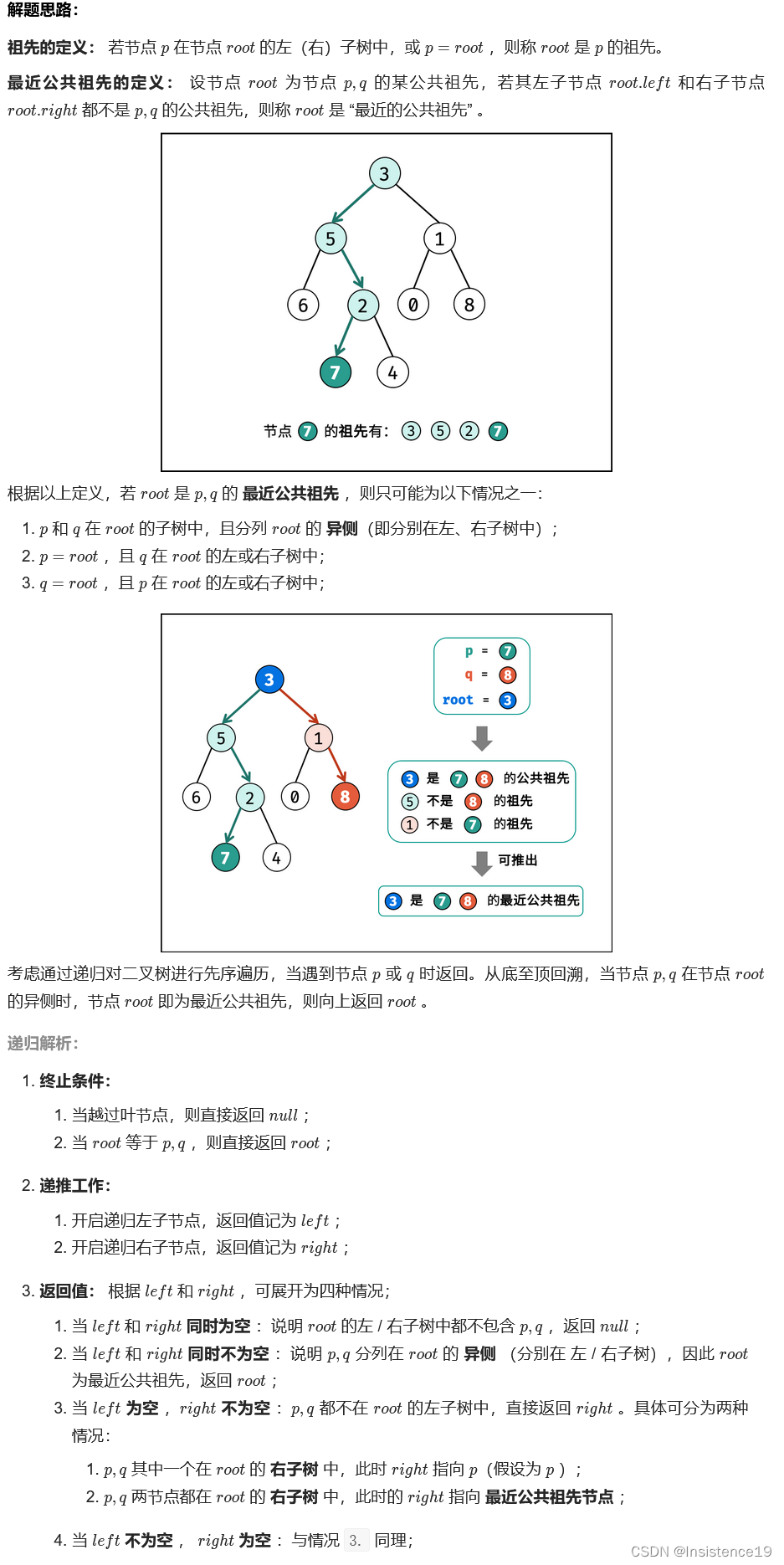
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == nullptr || root == p || root == q) return root;
        TreeNode *left = lowestCommonAncestor(root->left, p, q);
        TreeNode *right = lowestCommonAncestor(root->right, p, q);
        if(left == nullptr && right == nullptr) return nullptr; // 1.
        if(left == nullptr) return right; // 3.
        if(right == nullptr) return left; // 4.
        return root; // 2. if(left != null and right != null)
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/133608.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！