一 说明

前段时间放开疫情后，身边人基本都阳了，自己也不出所料阳了，然后去药店买温度计，发现买不到，网上的买了也不发货，但是看了温度计模块好像正常购买，于是想了一下，直接买个温度计模块自己diy一个温度计得了。

开源链接：https://gitee.com/jiangtao008/miniThermometer

二 成品效果

所有图片都在开源链接的pic文件夹中找到。

三 硬件材料

1、oled * 1

0.96尺寸，iic接口，12864分辨率。

2、红外测温传感器 * 1

购买链接：https://detail.tmall.com/item.htm?abbucket=11&id=687199263673&ns=1&spm=a230r.1.14.16.481725c1bhQuoe

3、按键 * 2

随意找两个按钮模块，找便宜的最好。

4、stm32最小系统 * 1

四 硬件连接

1、温度计连接stm32

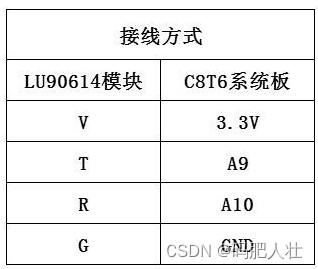
2、oled连接stm32

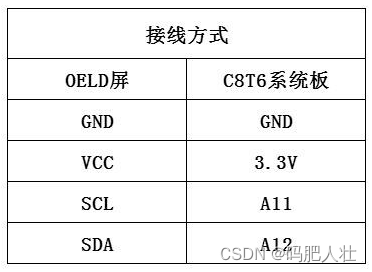
3、按按钮连接

连接stm32的A6、A7引脚。

五 软件

软件使用keil进行开发，源代码位于开源链接的SrcCode文件夹中；

开源链接：https://gitee.com/jiangtao008/miniThermometer

六 3D外盒模型

模型使用solidworks设计的，设计后直接使用3D打印机打印的外盒。

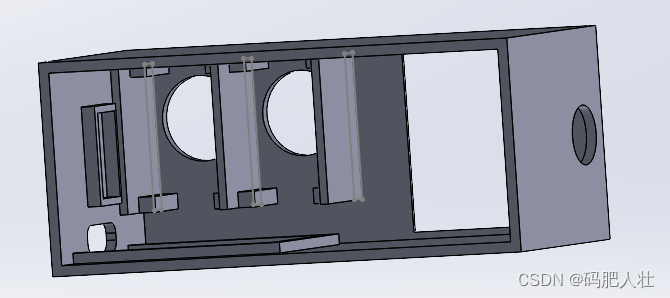
设计的源文件和stl文件在开源的3DModel文件夹中。