🐢🐢 基本概念-基本理论-基本方法 🐢🐢

---

660刷题记录 

二轮复刷标志

⭐：掌握不熟练

⭐⭐：是基本方法的组合，但没解出来

⭐⭐⭐：很难想到这种破局的手段

序号①、②：表示多种解法

加号+：一般表示多种基本方法的顺序组合，过于常见的基本方法已省去。

---

💥💥💥经典的错误-标准的零分 💥💥💥

1. 周期函数+奇函数  注：题干f(x)是以2为周期的周期函数这句话可以删去
2. 分段函数+复合函数
3. 
4. ①幂指函数→指数函数+换元（t→无穷大，尝试1/t→0代替）+洛必达②1^∞三部曲+有理运算法则
5. ①分子有理化②换元+洛必达or分子有理化③局部泰勒  ⭐
6. 倍角公式+局部泰勒（or洛必达但太复杂）⭐
7. 等价无穷小代换
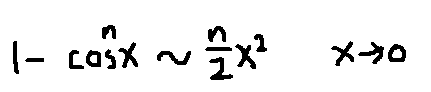
8. 幂指→指数+无穷大量的比较（除大头）
9. 待补充
10. ①拉格朗日定理+无穷大量的比较（除大头）②提项+幂指→指数
11. 幂指→指数+结论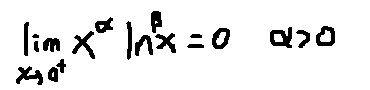：该结论证明：用洛必达⭐
12. 拉格朗日定理（or洛必达但太复杂）
13. 单调有界准则⭐
14. ①选填代特殊值直接秒②大题用“分母无穷小整体有极限则分子必然无穷小”
15. 凑要求的式子+有理运算法则拆开求极限（凑完也不能立马知道能不能拆开，拆开求极限后发现可以拆开）+洛必达⭐⭐⭐
16. ∞^0型用幂指→指数 +连续的概念（连续时，左极限=右极限=该处函数值）
17. 局部泰勒⭐
18. 分左右极限求极限的三种情况:分段（包括绝对值)+e^∞3+arctan∞
19. 
20. 待补充
21. 待补充
22. 极限的概念+分子无穷小整体有极限则分母必然无穷小
23. 
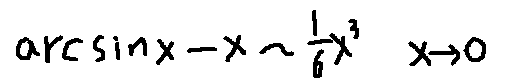
24. 二类四种间断点的概念
121. 利用反例判断极限相关命题⭐只用看第4个，两边都证否一下
122. 单调有界准则+归纳法+放缩⭐
123. 利用反例判断极限相关命题⭐⭐⭐要能想到这几个反例
124. f（x）在（a，b）上有界的充分必要条件是f（x）在（a，b）上连续且a点右极限和b点左极限存在。⭐
125. 极限的保序性（与极限保号性一块记忆，只需记一个A＞B，.....则f（x）＞f（y））⭐
126. 有理运算法则求极限+夹逼（包含放缩）+诱导公式+幂指→指数⭐⭐
127. ①无穷小阶的比较+换元+幂指→指数+拉格朗日+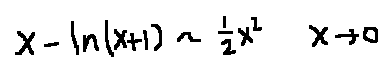②提项+局部泰勒⭐⭐
128. 单调有界准则+放缩（e^x≥1+x）⭐⭐⭐这里放缩是解决多个形如(1+x)乘积的关键。
129. 分左右极限求极限的三种情况:分段（包括绝对值)+e^∞3+arctan∞
130. 凑项+①换元+洛必达+有理运算法则求极限+等价无穷小代价②泰勒⭐⭐⭐这里凑项是利用“极限非零的因子的极限可以先求出来”，凑的是常数不影响原式。
131. 分子有理化+极限非零的因子的极限可以先求出来⭐
132. 拉格朗日中值定理
133. 幂指→指数+局部泰勒⭐
134. 极限非零的因子的极限可以先求出来+分母极限为0整体极限存在则分子极限为0+洛必达⭐