遗传算法python进阶理解+论文复现（纯干货，附前人总结引路）

一、简介和相关概念
- 遗传算法简介
- 相关概念介绍
二、与其他智能优化算法的比较
- 蚁群算法
- 粒子群优化算法
- 人工神经网络算法
- 模拟退火算法
- 鱼群算法
三、必学知识（站在前人的肩膀上）
四、python论文复现
五、遗传算法的改进（预告）

今天是2023年的第一天，首先祝各位兄弟姐妹们新年快乐，上学的学习进步，上班的工作顺心！我老早就想做一期遗传算法的讲解，内容主要是我在22年9月份时做的，当时因为太忙了没来得及搞，现在把它大概整理如下，供各位兄弟姐妹们参考！

时间隔得比较久，如有不足请在评论区或者私信我指出。

本文的大纲如上所示，首先是简要介绍下遗传算法的概念和与其他优化算法的比较，重点是后面两个，必学知识和一篇相关的论文复现。因为全网的资料比较多，我在学习的时候也参考了大量的博客，我会在第三部分给出博客的链接，这样会帮大家节省很多查找时间。第四部分是重中之重，我会给出复现论文的一些方法和思路，并且它具有一定的通用性。

一、简介和相关概念

遗传算法简介

遗传算法是一种智能优化算法，同时它也是一种找全局最优解的随机搜索算法，它可以用来求最值和求参。从名字来看，遗传算法借用了生物学里达尔文的进化理论：”适者生存，不适者淘汰“，将该理论以算法的形式表现出来就是遗传算法的过程。

遗传算法由美国的Holland教授提出，它是一种利用自然选择和生物进化思想在搜索空间搜索最优解的随机搜索算法。遗传算法通过模拟自然选择中的繁殖、交叉、变异的操作来寻求优良个体，用适应度函数评价个体优劣，依据优胜劣汰的原则，搜索出适应度较高的个体，并在搜索中不断增加优良个体的数量，循环往复，直至搜索出适应性最高的个体。遗传算法采用一种启发式搜索的方式进行群体搜索，易于并行化处理，尤其近年来随着计算机应用的发展，遗传算法的卓越性能引起人们的关注，被广泛应用于各个领域，如:函数优化、组合优化、图像处理等。¹

遗传算法是一种借鉴生物界自然选择和进化机制发展起来的高度并行、随机、自适应搜索算法。它使用群体搜索技术，将种群代表一组问题解，通过对当前种群施加选择、交叉和变异等一系列遗传操作，从而产生新一代种群，并逐步使种群进化到包含近似最优解的状态。²

第二种对遗传算法的解释来自于“一种基于遗传算法和高斯-牛顿法的合成算法在放射性药物生物动力学数据分析中的应用”这篇文章，这也是本文所要复现的文章，放在文章结尾的参考文献2处。

二、与其他智能优化算法的比较

下面介绍几种常见的智能优化算法：

蚁群算法

粒子群优化算法

人工神经网络算法

模拟退火算法

鱼群算法

1、蚁群算法 1992年，意大利学者Colorni A、Dorigo M、Maniezzo V提出了蚁群算法。在寻找食物源的过程中，蚁群总能找到一条最短路径（从蚁巢到食物源)，蚁群算法主要是利用蚁群的这种寻优能力来解决一些离散系统优化中的困难问题。蚁群算法已经成功地应用于解决旅行商问题、调度问题等等，并且取得了很好的效果。但是，蚁群的研究刚刚起步，没有坚实的数学基础，算法在收敛性、理论依据等方面还需要进一步地研究。
2、粒子群优化算法 Kenney和 Eberhart在1995年提出了一种优化技术——粒子群优化算法。它主要基于对鸟类捕食行为的研究,通过对随机产生的一组初始解进行迭代,以此来寻求最优解。粒子群算法称优化问题的解为“粒子”，每个粒子都拥有一个决定粒子飞翔的方向和距离的速度及一个由被优化的函数决定的适应值，在解空间中，所有粒子都随着最优粒子的运动进行搜索。在迭代的过程中，粒子不断地更新自己，这主要通过对两个极值的追踪来进行，一个是全局极值,即整个种群到目前为止找到的最优解，另一个是个体极值，即粒子本身找到的最优解。当然，也可以只利用部分粒子，此时的极值叫局部极值。
3、人工神经网络算法
人工神经网络是目前比较热门的一个研究领域。人工神经网络是利用生物学中的神经网络原理建立起来的一种并行分布处理系统，是一个由很多多输入、单输出的神经元组成的网络，神经元的输入会有一些连接通道，他们分别对应一个连接权系数。人工神经网络通过不断地学习来确定它的权值，这个学习过程称为训练，其学习方式分为有导师的学习和无导师的学习两种。这两种方式的不同在于是不是有目标输出与输入相对应，并且对训练是不是进行了指导。有导师的学习有目标输出和输入，并对训练进行了指导，无导师的学习则相反。
4、模拟退火算法
1953年，Metropolis提出了模拟退火的思想，Kirkpatrick在1983年将退火思想引入了组合优化的领域，并取得了成功。模拟退火算法是局部搜索算法的扩展，所以理论上来说它是一种全局最优算法。模拟退火算法基于固体物质的退火原理。物质在高温的状态下进行无序的、强烈的热运动，故开始时，让固体有较高的温度，然后缓慢降温，直到物质慢慢变为平衡且有序的状态，最后则在能量最小时达到基态，这就是所说的退火。模拟退火算法在高温下通过采用Metropolis抽样准则来搜索最优解，这个过程是随机的，在这个过程中，它利用降温的过程进行重复抽样，进而搜索相近的最优值。模拟退火算法能有效寻找全局最优解，但是也存在一定的缺点，比如：收敛速度较慢等。
5、鱼群算法
2002年，李晓磊博士提出了鱼群算法，这是人工智能的又一个典型的应用，它通过模拟鱼群的觅食行动和生存活动进行全局寻优，即算法首先构造动物的简单的底层行为，然后对个体均进行局部寻优，逐步搜寻出全局最优值。鱼群算法搜索全局极值的能力较强，能防止局部极值的产生；对搜索空间而言有较强的自适应能力;收敛速度较快,并且在精度要求不高的情况下，能很快地得到可行解；对问题要求不严格，不需要精确地描述，也不需要严格的机理模型，这使得鱼群算法的应用范围得到了更大的扩展。目前，鱼群算法已经被广泛地应用于解决连续优化问题系统辨识问题、组合优化问题、神经网络训练和电力系统无功优化等问题，并且效果良好。

三、必学知识（站在前人的肩膀上）

我在学习遗传算法的时候同样在CSDN和其他网站上参考了大量博客，因为需要复现自己找的论文，所以需要搞懂它的原理。

我找文章花了很多时间，但真正有帮助的非常有限。大部分有用的文章都是在CSDN上找的，下面给出我的一些经验和链接，看透这几篇，再用程序复现一下，我相信兄弟姐妹们基本上都能理解，能够为大家节省大量的时间。（当然也有其他很好的博客，可能目前我还未找到）

理解遗传算法的原理，搞懂它到底是怎么操作的，选择、交叉、变异到底是毛意思，看知乎上的这篇：遗传算法python（含例程代码与详解)。尤其是看这篇文章的第三部分：算法实例，搞懂怎么用遗传算法求x^2的极值后，我相信你已经入门了。
搞懂遗传算法的代码，学会用python代码来求极值，看这篇：遗传算法详解附python代码实现。我找了很多写遗传算法的代码的文章，但是我觉得都不如这篇文章清晰简洁。这位大兄弟用一个求函数极值的例子来讲解，代码的原理和逻辑非常清晰，能够成功复现，我的论文复现主要就是参考这篇代码，它的通用性很强。
还有其他的一些博客，可以作为补充参考：
遗传算法求解香蕉函数极大值
遗传算法详解python代码实现以及实例分析
matlab选手看这篇：遗传算法小结及算法实例（附Matlab代码）
python遗传算法（详解）
超参数寻优遗传算法（GA）超参数寻优的python实现
上文说到的除了常见的二进制编码法等，还有诸如格雷码、浮点编码法、符号编码法等。想要了解其他的编码方式和常用的选择算子看这篇：遗传算法（Genetic Algorithms）的全面讲解及python实现

虽然上面给出了很多参考博客，但是我最推荐的还是前两个，吃透前两个博客就搞懂了遗传算法的原理和代码逻辑，其他博客的可做补充说明来看。由于本文不讲遗传算法的基础知识，请兄弟姐妹们把这些知识补齐后再看本文，本文会给出在此基础上的，我对于遗传算法的理解。

四、python论文复现

复现的论文为参考文献1中的遗传算法部分，先将文章的部分内容截图如下：
第一个大头是目标函数，文章给出的目标函数为：
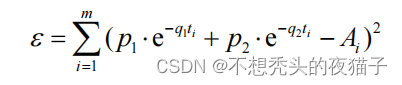
在这里插入图片描述
其中， $t_{i}$ 和 $A_{i}$ 是已知的，如下图所示， $t_{i}$ 表示第i个测量时刻， $A_{i}$ 表示第i个时刻所对应的器官内的血药浓度值：

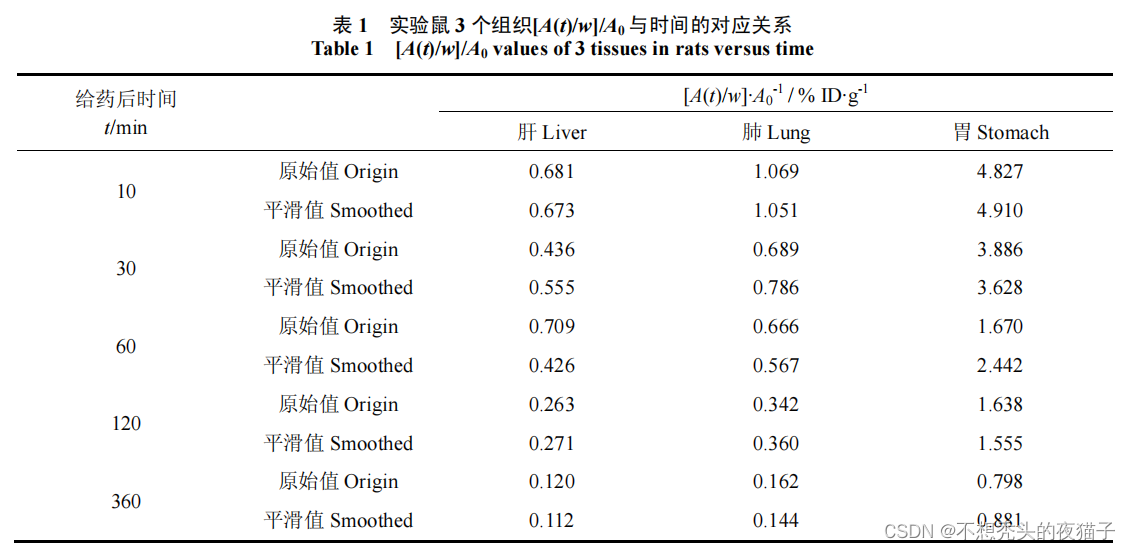
文章给出了大鼠三个器官分别在第10、30、60、120、360分钟的血药浓度值。因此在上述的目标函数中，对于每一个器官，我都可以建立一个模型，m=5， $t_{i}$ 和 $A_{i}$ 是已知的，此时只有 $p_{1}$ 、 $p_{2}$ 、 $q_{1}$ 、 $q_{2}$ 是未知的，也是我们要求的四个参数，因此我们能够得到一个关于 $p_{i}$ 、 $q_{i}$ 的四元函数表达式 $\xi$ ( $p_{1}$ , $p_{2}$ , $q_{1}$ , $q_{2}$ )，目标就是求当 $\xi$ 达到最小时， $p_{1}$ 、 $p_{2}$ 、 $q_{1}$ 、 $q_{2}$ 这四个参数值。

本文本质上是求四元函数的极小值，对5组数据需要分别代入再进行求和，因此目标函数可设为：

dic_liver = {0.167: 0.681, 0.5: 0.436, 1: 0.709, 2: 0.263, 6: 0.12}  # 键表示时间（h),值表示肝内的浓度
dic_lung = {0.167: 1.069, 0.5: 0.689, 1: 0.666, 2: 0.342, 6: 0.162}  # 表示肺内的浓度
dic_stomach = {0.167: 4.827, 0.5: 3.866, 1: 1.67, 2: 1.638, 6: 0.798}  # 表示胃内的浓度的


def F(p1, p2, q1, q2):  # 设计目标函数 法一
    fun = 0
    for key, value in dic_liver.items():
        fun = ((p1 * np.exp(-q1 * key) + p2 * np.exp(-q2 * key)) - value) ** 2 + fun
    return fun


def F2(p1, p2, q1, q2):  # 设计目标函数 法二
    l1 = list(dic_liver.keys())
    l2 = list(dic_liver.values())
    result = [((p1 * np.exp(-q1 * i) + p2 * np.exp(-q2 * i)) - j) ** 2 for i, j in zip(l1, l2)]
    # result = sum(result)
    total = 0
    for i in range(len(result)):
        total = total + result[i]
    return total

简要分析下：前三个字典是文章中给出的数据，描述了时间和对应血药浓度的关系，本文用字典类型，用键表示给药时间（文章以分钟为单位，这里把它都除以60标准化，以h为单位）。我在设计目标函数时用了两种方法，都要用到字典类型，但是方法一明显更简洁些。

适应度函数可设为（这里是求最小值对应的适应度函数）：

def get_fitness(pop):
    p1, p2, q1, q2 = translateDNA(pop)
    pred = F(p1, p2, q1, q2)
    return -(pred - np.max(pred)) + 1e-3  # 要加上一个很小的正数

第二个大头就是编码和解码过程，通常来说，我们应首先随机生成十进制的初始种群，然后将十进制编码为二进制进行交叉、变异等操作，完成后再将二进制解码为十进制。但是实际上，第一步（随机生成十进制数）可以去掉，因为我们可以在程序中直接随机生成二进制串，因此编码过程变得很简单，这里只需要重点关注解码过程。以我复现的这篇文章为例：

在这里插入图片描述

一个参数对应的二进制长度为20位，本文有4个参数，那么对于这个二进制的初始种群来说，每一行就有（20*4）80位。而本文要求初始种群包含150个个体，实际上就是有150组解（ $p_{1}$ , $p_{2}$ , $q_{1}$ , $q_{2}$ ），则列数为150，行数为80，因此最终应该形成一个150*80的0-1矩阵。

注：如果看了上面推荐的两篇博客就知道，一个十进制的数可以根据“除2取余，逆序排列”转换为任意位数的二进制，只要在高位上补0就行了。当二进制的长度越长，计算越复杂，但精度也越高。

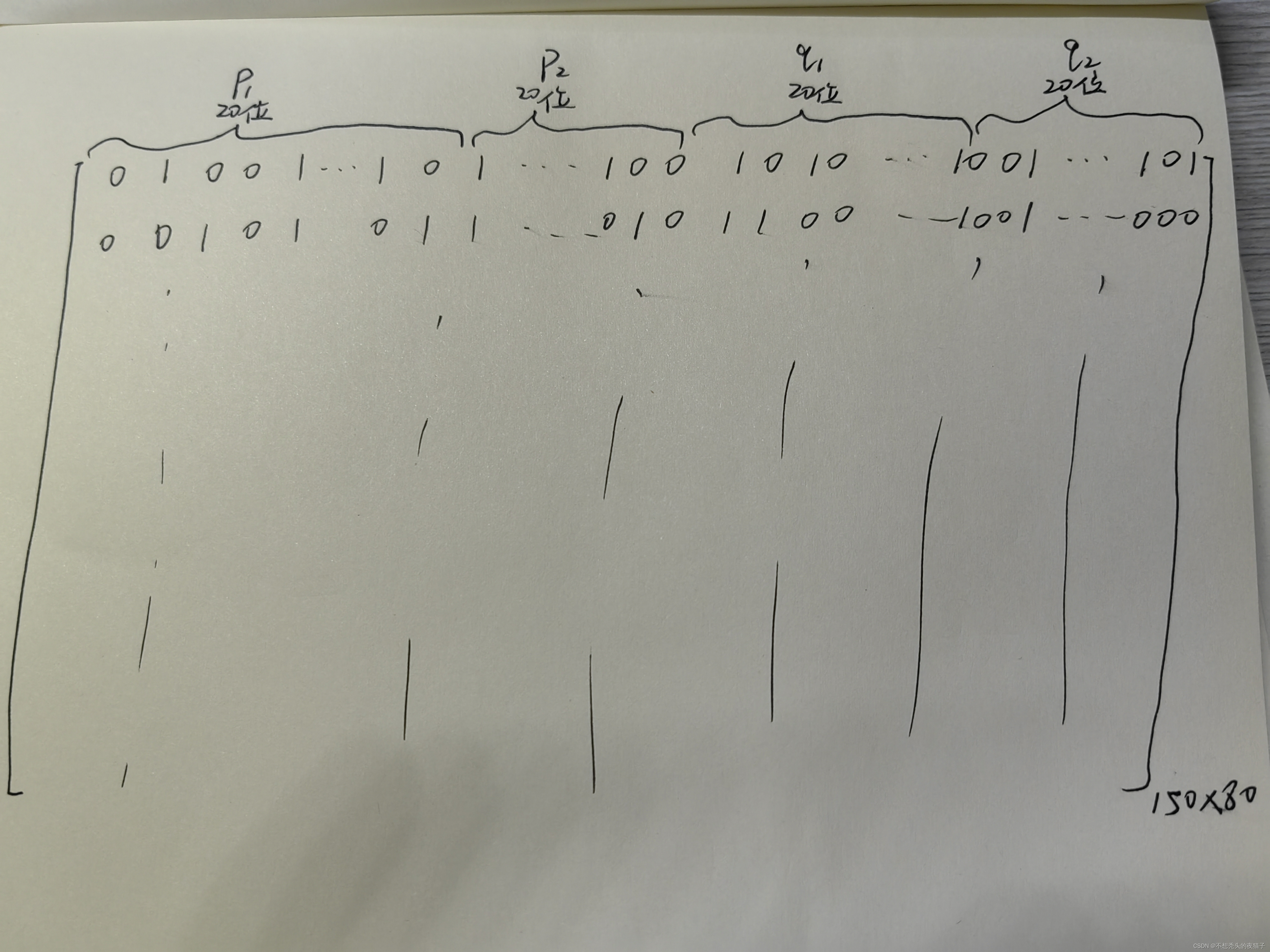
在这里插入图片描述
生成二进制初试种群代码如下：

pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE * 4))  
# matrix (POP_SIZE, DNA_SIZE) POP_SIZE为150，DNA_SIZE为20

解码过程如下：

def translateDNA(pop):  # 解码 pop表示种群矩阵，一行表示一个二进制编码表示的DNA，矩阵的行数为种群数目数为每个DNA长度*DNA个数
    p1_pop = pop[:, :20]
    p2_pop = pop[:, 20:40]
    q1_pop = pop[:, 40:60]
    q2_pop = pop[:, 60:]

    # 解码过程，并将pi和qi转换到规定的范围中去
    p1 = p1_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (p1_BOUND[1] - p1_BOUND[0]) + p1_BOUND[
        0]
    p2 = p2_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (p2_BOUND[1] - p2_BOUND[0]) + p2_BOUND[
        0]
    q1 = q1_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (q1_BOUND[1] - q1_BOUND[0]) + q1_BOUND[
        0]
    q2 = q2_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (q2_BOUND[1] - q2_BOUND[0]) + q2_BOUND[
        0]
    return p1, p2, q1, q2

两个大头根据自己的实际问题修改完后，剩下的基本可以套代码了。但是要注意一点，在遗传算法中，产生交叉和变异的位置都是随机的，比如我DNA序列的长度为80，则需要将产生随机数的范围修改到（0,80）。
cross_points = np.random.randint(low=0, high=DNA_SIZE * 4)

其他的长度以此类推。

下面附上完整代码，相关的初试参数设置均来源于复现论文，再次感谢遗传算法详解附python代码实现的大兄弟，为我的复现提供了很多参考：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import warnings

warnings.filterwarnings('ignore')

DNA_SIZE = 20  # DNA长度（二进制编码长度）
POP_SIZE = 150  # 初始种群数量
CROSSOVER_RATE = 0.95  # 交叉率
MUTATION_RATE = 0.005  # 变异率 将0.005改为0.01
N_GENERATIONS = 1000  # 进化代数 进化代数在 800—1200 之间比较适合，本文选取进化1000代
p1_BOUND = [0, 1]  # 确定参数的范围
p2_BOUND = [0, 1]
q1_BOUND = [0, 1]
q2_BOUND = [0, 1]

dic_liver = {0.167: 0.681, 0.5: 0.436, 1: 0.709, 2: 0.263, 6: 0.12}  # 键表示时间（h),值表示肝内的浓度
dic_lung = {0.167: 1.069, 0.5: 0.689, 1: 0.666, 2: 0.342, 6: 0.162}  # 表示肺内的浓度
dic_stomach = {0.167: 4.827, 0.5: 3.866, 1: 1.67, 2: 1.638, 6: 0.798}  # 表示胃内的浓度的


def F(p1, p2, q1, q2):  # 设计目标函数 法一
    fun = 0
    for key, value in dic_liver.items():
        fun = ((p1 * np.exp(-q1 * key) + p2 * np.exp(-q2 * key)) - value) ** 2 + fun
    return fun


def F2(p1, p2, q1, q2):  # 设计目标函数 法二
    l1 = list(dic_liver.keys())
    l2 = list(dic_liver.values())
    result = [((p1 * np.exp(-q1 * i) + p2 * np.exp(-q2 * i)) - j) ** 2 for i, j in zip(l1, l2)]
    # result = sum(result)
    total = 0
    for i in range(len(result)):
        total = total + result[i]
    return total

# 求最小值对应的适应度函数 
def get_fitness(pop):
    p1, p2, q1, q2 = translateDNA(pop)
    pred = F(p1, p2, q1, q2)
    return -(pred - np.max(pred)) + 1e-3  # 要加上一个很小的正数

def translateDNA(pop):  # 解码 pop表示种群矩阵，一行表示一个二进制编码表示的DNA，矩阵的行数为种群数目 即行数为150行，列数为每个DNA长度*DNA个数，即20*4=80列（150*80）
    p1_pop = pop[:, :20]
    p2_pop = pop[:, 20:40]
    q1_pop = pop[:, 40:60]
    q2_pop = pop[:, 60:]

    p1 = p1_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (p1_BOUND[1] - p1_BOUND[0]) + p1_BOUND[
        0]
    p2 = p2_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (p2_BOUND[1] - p2_BOUND[0]) + p2_BOUND[
        0]
    q1 = q1_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (q1_BOUND[1] - q1_BOUND[0]) + q1_BOUND[
        0]
    q2 = q2_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (q2_BOUND[1] - q2_BOUND[0]) + q2_BOUND[
        0]
    return p1, p2, q1, q2

# 以下函数包含两个功能，交叉和变异
def crossover_and_mutation(pop, CROSSOVER_RATE=0.95):  # 单点交叉
    new_pop = []
    for father in pop:  # 遍历种群中的每一个个体，将该个体作为父亲
        child = father  # 孩子先得到父亲的全部基因（这里我把一串二进制串的那些0，1称为基因）
        if np.random.rand() < CROSSOVER_RATE:  # 产生子代时不是必然发生交叉，而是以一定的概率发生交叉
            mother = pop[np.random.randint(POP_SIZE)]  # 再种群中选择另一个个体，并将该个体作为母亲
            cross_points = np.random.randint(low=0, high=DNA_SIZE * 4)  # 随机产生交叉的点
            child[cross_points:] = mother[cross_points:]  # 孩子得到位于交叉点后的母亲的基因
        mutation(child)  # 每个后代有一定的机率发生变异
        new_pop.append(child)

    return new_pop


# 基本位变异算子
def mutation(child, MUTATION_RATE=0.005):
    if np.random.rand() < MUTATION_RATE:  # 以MUTATION_RATE的概率进行变异
        mutate_point = np.random.randint(0, DNA_SIZE * 4)  # 随机产生一个实数，代表要变异基因的位置
        child[mutate_point] = child[mutate_point] ^ 1  # 将变异点的二进制为反转（异或运算符 1与1为0、1与0为1、0与0为0）


def select(pop, fitness):  # 描述了从np.arange(POP_SIZE)里选择每一个元素的概率，概率越高约有可能被选中，最后返回被选中的个体即可
    idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
                           p=(fitness) / (fitness.sum()))
    return pop[idx]

# # np.random.choice()函数的用法
# arr = ['pooh', 'rabbit', 'piglet', 'Christopher']
# np.random.choice(aa_milne_arr, size=11, p=[0.5, 0.1, 0.1, 0.3])


def print_info(pop):
    fitness = get_fitness(pop)
    min_fitness_index = np.argmin(fitness)  # 表示为array的最大值/最小值对应的索引
    print("min_fitness:", fitness[min_fitness_index])
    p1, p2, q1, q2 = translateDNA(pop)
    print("最优的基因型：", pop[min_fitness_index])
    print("(p1, p2, q1, q2):",
          (p1[min_fitness_index], p2[min_fitness_index], q1[min_fitness_index], q2[min_fitness_index]))

if __name__ == "__main__":

    pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE * 4))  # matrix (POP_SIZE, DNA_SIZE) POP_SIZE为150，DNA_SIZE为20
    for _ in range(N_GENERATIONS):  # 迭代N代
        pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))  # 进行交叉和变异
        fitness = get_fitness(pop)
        pop = select(pop, fitness)  

    print_info(pop)

相对于原博客来说，对于相对较难理解的部分，我给代码加上了必要的注释，能够方便大家理解。

以肝器官为例，程序的运行结果，最优的基因型是p1,p2,q1,q2所对应的二进制位数，下面是把它们解码为十进制后的结果：
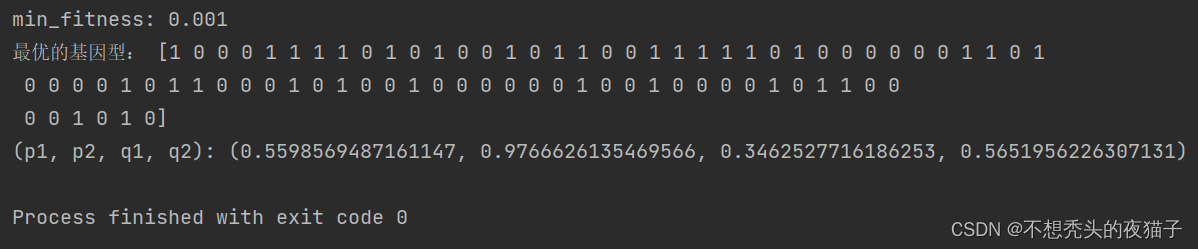
在这里插入图片描述
虽然跟原文的结果有一定出入，但是第一步，已经能够跑出来了。之后我们再对其进行修改完善。

交叉算法有单点交叉、多点交叉、均匀交叉等，本文用的方法时多点交叉。同理，变异的操作也不只这一种，本文所用的交叉、变异都是最常用的操作。

五、遗传算法的改进（预告）

要想使得程序获得更快更好的效果，我们需要对其进行改进。各位兄弟姐妹们先把本文搞懂，下篇文章我会综合找到的一些文献来介绍对遗传算法的改进和它的python程序实现。对遗传算法的改进主要有以下三部分：

适应度函数的改进
交叉概率的改进
变异概率的改进

不知道代码是否容易理解，若需要复现论文的讲解，可以在评论区留言或者私信我，如果人数多的话，可以做一期讲解视频，希望对各位兄弟姐妹们有所帮助！

李延梅. 一种改进的遗传算法及应用[D].华南理工大学,2012. ↩︎ ↩︎
孙亮,李君利,程建平.一种基于遗传算法和高斯-牛顿法的合成算法在放射性药物生物动力学数据分析中的应用[J].核技术,2006(12):927-931.
遗传算法python（含例程代码与详解)
遗传算法详解附python代码实现
遗传算法求解香蕉函数极大值
遗传算法详解python代码实现以及实例分析
遗传算法小结及算法实例（附Matlab代码）
python遗传算法（详解）
超参数寻优遗传算法（GA）超参数寻优的python实现
遗传算法（Genetic Algorithms）的全面讲解及python实现 ↩︎