目录

1. 用栈实现队列

         1.1 题目描述

1.2 栈和队列的基础知识

1.3 思路分析

2. 扩展题目——用队列实现栈

2.1 题目描述

2.2 思路分析

---

1. 用栈实现队列

原题链接：

剑指 Offer 09. 用两个栈实现队列 - 力扣（LeetCode）https://leetcode.cn/problems/yong-liang-ge-zhan-shi-xian-dui-lie-lcof/submissions/

1.1 题目描述

用两个栈实现一个队列。请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

1.2 栈和队列的基础知识

栈是一种非常常见的数据结构，他在计算机领域被广泛应用，比如操作系统会给每一个线程创建一个栈用来存储函数调用时各个函数的参数，返回地址及临时变量等。栈的特点是先进后出，即最后被压入栈的元素会被第一个弹出。栈一般用顺序表实现。

栈通常是一个不考虑排序的数据结构，我们需要O(N)的时间复杂度才能找到一个元素，如果想要在O(1)的时间内找到，那么栈需要进行特殊处理。等刷题刷到后面再讲！

队列呢？与栈似乎截然不同，队列的特点是先进先出，即第一个入队列的元素会第一个出来。队列的实现我们一般用一个带头指针和尾指针的链表来实现。

1.3 思路分析

一个队列里面包含了两个栈，stack1和stack2。直讲解有点抽象，我们用一个具体的例子来讲解。

假设我们要向队列中插入，1,2,3三个元素后将它们删除，如何实现呢？

首先，我们插入1这个元素，不妨把他插入到stack1，然后再依次插入，2，3，此时stack1内栈顶元素为3，stack2为空（见下图）。

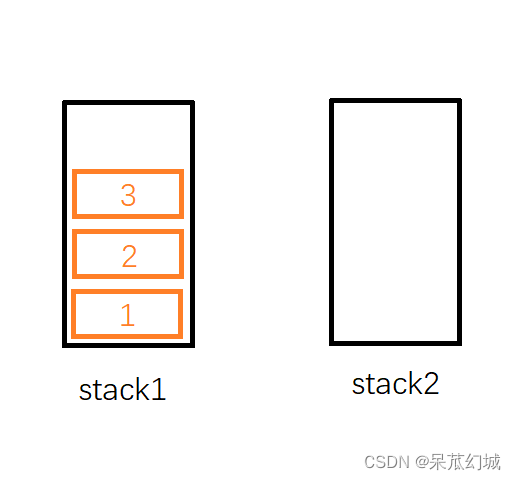
这时候，我们尝试从队列中删除一个元素。按照队列先入先出的规则，最先入列的1应该是最先出列的，故应该删除1。但是1存储在stack1中并不是在栈顶，于是我们需要借助stack2：如果我们把stack1中的元素依次弹出，并压入到stack2中，则stack2中的元素顺序正好和原来相反。因此经过三次弹出stack1和压入stack2的操作后，stack1为空，stack2中的元素是 3,  2,  1，这时候就可以弹出栈顶的1了。

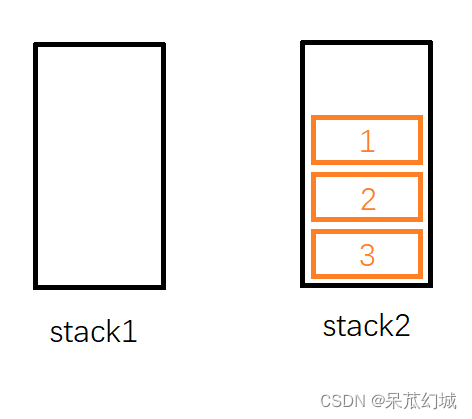
在删除队头的1后，队列中还剩2和3，我们想要继续删除队头的元素，那么应该删除2，而此时2恰好又在栈顶，因此直接弹出2即可。

 

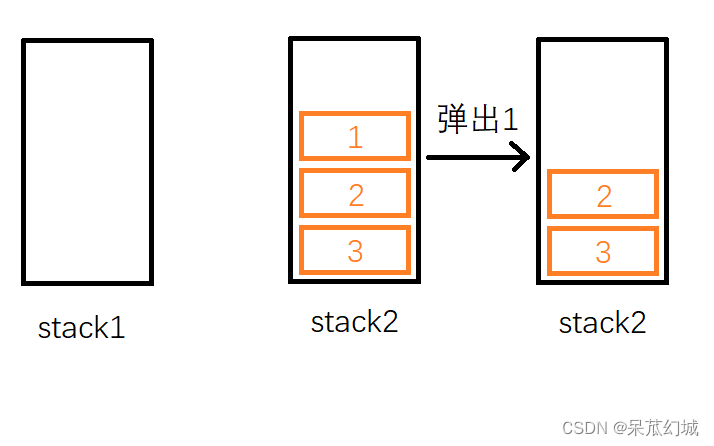
 通过例子的分析我们就可以总结如下规律：

添加元素的步骤：直接将元素入栈到stack1即可。

删除元素的步骤：当stack2不为空时，在栈顶的元素就是队列中先入列的元素，直接弹出栈顶的元素即可；当stack2为空时，我们就需要将stack1中的元素依次弹出并压入到stack2中，直到stack1为空。如果说stack2为空，去stack1中拿元素时发现stack1也为空，根据题目要求返回-1即可。

销毁队列：销毁两个栈即可。

//栈的代码
/
typedef int ST_DATA_TYPE;

typedef struct Stack
{
	ST_DATA_TYPE* data;
	int size;
	int capacity;
} ST;

//栈的初始化
void StackInit(ST* st)
{
	ST_DATA_TYPE* newlist = (ST_DATA_TYPE*)malloc(sizeof(ST_DATA_TYPE) * 4);
	if (newlist != NULL)
	{
		st->data = newlist;
		st->capacity = 4;
		st->size = 0;
	}
}

//销毁栈
void StackDestory(ST* st)
{
	free(st->data);
	st->data = NULL;
}

//入栈
void StackPush(ST* st, ST_DATA_TYPE x)
{
	if (st->size == st->capacity)
	{
		ST_DATA_TYPE* newlist = (ST_DATA_TYPE*)realloc(st->data, sizeof(ST_DATA_TYPE) * 2 * st->capacity);
		if (newlist == NULL)
		{
			perror("malloc");
		}
		else
		{
			st->data = newlist;
			st->capacity *= 2;
		}
	}
	st->data[st->size] = x;
	st->size++;

}

//出栈
void StackPop(ST* st)
{
	assert(st->size > 0);
	st->size--;
}

//查看栈顶元素
ST_DATA_TYPE StackTop(ST* st)
{
	assert(st->data);
	return st->data[st->size - 1];
}

//栈的大小
int StackSize(ST* st)
{
	assert(st->data);
	return st->size;
}

//判断栈是否为空
bool StackEmpty(ST* st)
{
	assert(st->data);
	return st->size == 0;
}

/

//定义队列
typedef struct {
	ST stack1;
	ST stack2;
} CQueue;


//初始化队列
CQueue* cQueueCreate() {
	CQueue* q1 = (CQueue*)malloc(sizeof(CQueue));
	StackInit(&q1->stack1);
	StackInit(&q1->stack2);
	return q1;
}

//入列
void cQueueAppendTail(CQueue* obj, int value) {
	StackPush(&obj->stack1, value);
}

//出列
int cQueueDeleteHead(CQueue* obj) {
	assert(obj);
	if (StackEmpty(&obj->stack2))
	{
        if(StackEmpty(&obj->stack1))
        {
            return -1;
        }
        else
        {
            while (!StackEmpty(&obj->stack1))
		    {
                int top = StackTop(&obj->stack1);
                StackPop(&obj->stack1);
                StackPush(&obj->stack2, top);
		    }
        }
	}
	int top = StackTop(&obj->stack2);
	StackPop(&obj->stack2);
	return top;
}

//销毁队列
void cQueueFree(CQueue* obj) {
	StackDestory(&obj->stack1);
	StackDestory(&obj->stack2);
}

2. 扩展题目——用队列实现栈

原题链接：

力扣https://leetcode.cn/problems/implement-stack-using-queues/

2.1 题目描述

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
bool empty() 如果栈是空的，返回 true ；否则，返回 false 。

2.2 思路分析

一个栈里面包含了两个队列，Queue1和Queue2，直接讲解也是有点抽象，我们通过例子来讲解：

假设我们要依次入栈1,  2，3

首先入栈元素1，同样，我们不妨直接把他插入Queue1中，然后再次插入2,  3到Queue1中，此时Queue1中有三个元素1,  2,  3，Queue2为空。

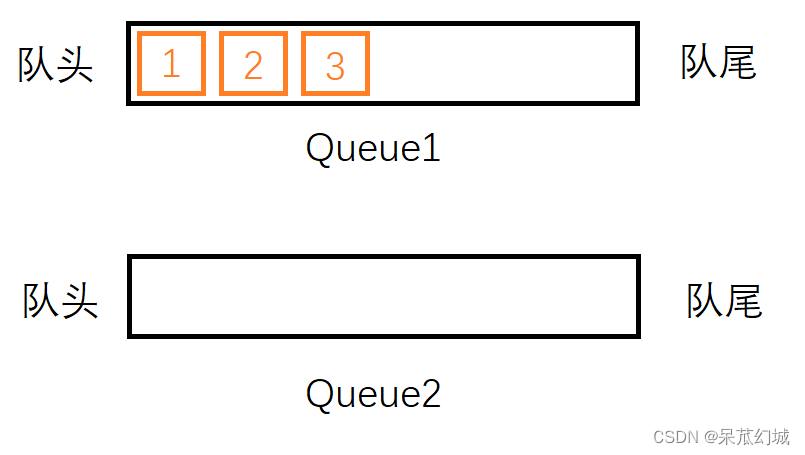
 现在，我们尝试从栈中删除一个元素。按照栈后进先出的规则，最后入栈的元素3应该最先出栈。但是元素3并不在Queue1的队头，我们不能直接把他删除。这时候我们就要借助Queue2了：将元素1从Queue1中出列，将它入列到Queue2中；将元素2从Queue1中出列将它入列到Queue2中，此时我们会发现，要出栈的元素3就在Queue1的队头了，直接将其出列即可。

 同样地，我们还想删除一个元素，此时2就是栈顶元素，它不在Queue2的队头不能直接删除，同样需要借助另一个队列Queue1，将元素1从Queue2中出列，入列到Queue1中，此时要出栈的元素2，就在Queue2的队头了，直接删除即可。

 还想删除栈顶的元素1时，我们发现它就在Queue1的队头直接删除即可。

通过以上分析我们总结出一下规律：

删除元素：将不为空的那个队列数据的N-1（N为不为空的那个队列的元素个数/队列大小）个导入到为空的那个队列，剩下的那个元素即为栈顶元素，删除即可。

添加元素：将元素添加到那个不为空的队列中即可，如果两个都为空，随便添加到哪一个都行。

查看栈顶的元素：根据以上分析：不为空的那个队列队尾的数据就是栈顶的元素，我们直接查看队尾的元素即可。

判断栈是否为空：如果两个队列都为空，则栈为空，否则栈不为空。

销毁栈：销毁两个队列即可。

//队列的代码
/
typedef  int Q_DATA_TYPE;

typedef struct QueueNode
{
	struct QueueNode* next;
	Q_DATA_TYPE data;
} QNode;

typedef struct QueuePointer
{
	QNode* head;
	QNode* tail;

} QP;

void QueueInit(QP* qp)
{
	assert(qp);
	qp->head = qp->tail = NULL;
}

void QueuePush(QP* qp, Q_DATA_TYPE x)
{
	assert(qp);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		printf("malloc failed\n");
		exit(-1);
	}
	newnode->next = NULL;
	newnode->data = x;
	if (qp->head == NULL)
	{
		qp->head = qp->tail = newnode;
	}
	else
	{
		qp->tail->next = newnode;
		qp->tail = newnode;
	}
}

void QueuePop(QP* qp)
{
	assert(qp);
	assert(qp->head);
	if (qp->head->next == NULL)
	{
		free(qp->head);
		qp->head = qp->tail = NULL;
	}
	else
	{
		QNode* next = qp->head->next;
		free(qp->head);
		qp->head = next;
	}

}

Q_DATA_TYPE QueueFront(QP* qp)
{
	assert(qp);
	assert(qp->head);
	return qp->head->data;
}

Q_DATA_TYPE QueueBack(QP* qp)
{
	assert(qp);
	assert(qp->tail);
	return qp->tail->data;
}

bool QueueEmpty(QP* qp)
{
	assert(qp);
	return qp->head == NULL;
}

void QueueDestory(QP* qp)
{
	assert(qp);

	QNode* cur = qp->head;
	while (cur != NULL)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	qp->head = qp->tail = NULL;
}

int QueueSize(QP* qp)
{
	assert(qp);

	int size = 0;
	QNode* cur = qp->head;
	while (cur)
	{
		++size;
		cur = cur->next;
	}
	return size;
}
/

//定义栈
typedef struct {
    QP Queue1;
    QP Queue2;

} MyStack;

//栈的初始化
MyStack* myStackCreate() {
    MyStack* ps = (MyStack*)malloc(sizeof(MyStack));
    if(ps==NULL)
    {
        printf("malloc failed");
        exit(-1);
    }
    else
    {
        QueueInit(&ps->Queue1);
        QueueInit(&ps->Queue2);
    }
    return ps;
}

//入栈
void myStackPush(MyStack* obj, int x) {

    if(QueueEmpty(&obj->Queue1))
    {
        QueuePush(&obj->Queue2,x);
    }
    else
    {
        QueuePush(&obj->Queue1,x);
    }
}

//出栈
int myStackPop(MyStack* obj) {
    QP*emptyq = &obj->Queue1; //假设Queue1为空，Queue2不为空
    QP*noneemptyq = &obj->Queue2;
    if(!QueueEmpty(&obj->Queue1)) //用if对假设进行修正
    {
        emptyq= &obj->Queue2;
        noneemptyq = &obj->Queue1;
    }
    while(QueueSize(noneemptyq)>1) //将不为空的那个队列导入到为空的那个
    {
        QueuePush(emptyq,QueueFront(noneemptyq));
        QueuePop(noneemptyq);
    }
    int a = QueueFront(noneemptyq); //记录原来不为空的那个队列的对头元素，然后删除
    QueuePop(noneemptyq);
    return a;
}
//查看栈顶元素
int myStackTop(MyStack* obj) {
    if(!QueueEmpty(&obj->Queue1))
    {
        return QueueBack(&obj->Queue1);
    }
    else
    {
        return QueueBack(&obj->Queue2);
    }
}
//判断栈是否为空
bool myStackEmpty(MyStack* obj) {
    return QueueEmpty(&obj->Queue1) && QueueEmpty(&obj->Queue2);
}
//销毁栈
void myStackFree(MyStack* obj) {
    QueueDestory(&obj->Queue1);
    QueueDestory(&obj->Queue2);
    free(obj);
}