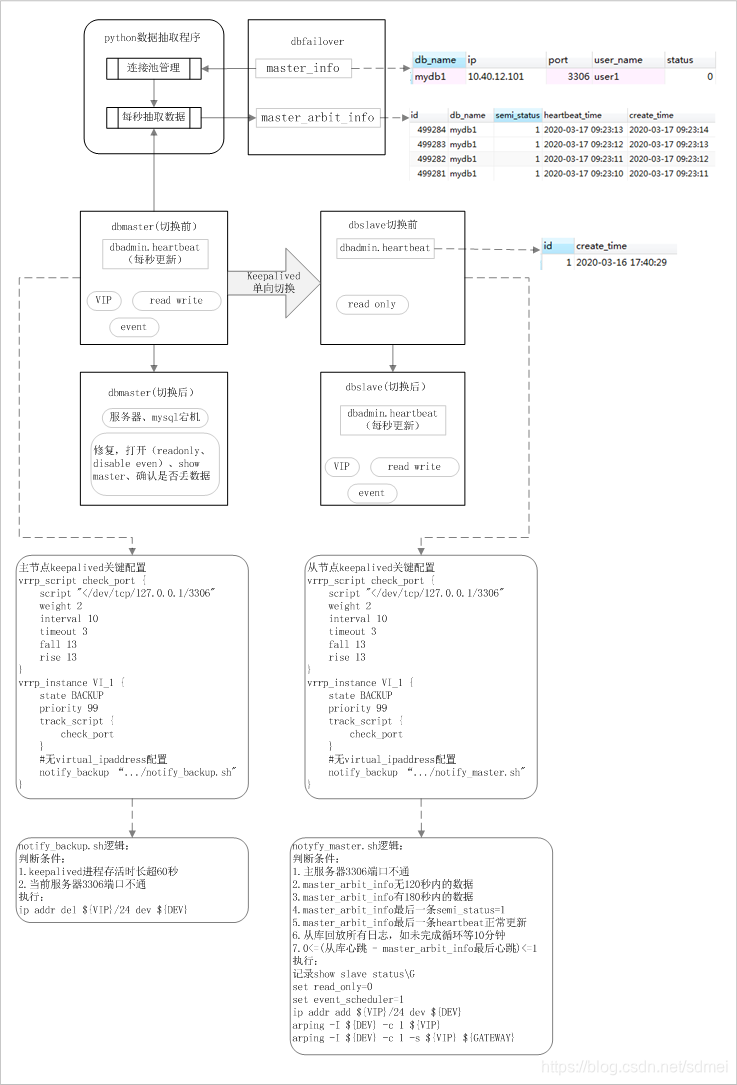
( A, B )---1*30*2---( 1, 0 )( 0, 1 )
让网络的输入只有1个节点,AB各由7张二值化的图片组成,排列组合A和B的所有可能性,固定收敛误差为7e-4,统计收敛迭代次数
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 迭代次数 | |
| 1b | 1b | 1b | 1b | 1b | 1b | 0 | 0*0*0*0*0*0*0-1*1*1*1*1*1*0 | 19807.77889 |
如0*0*0*0*0*0*0与1*1*1*1*1*1*0分类收敛误差为7e-4时,收敛199次,平均迭代次数为19807。
不同的数据共收集到了33组
| 差值结构 | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 迭代次数 | 等位点数值差 | |||
| 1b | 1b | 1b | 1b | 1b | 1b | 0 | 0*0*0*0*0*0*0-1*1*1*1*1*1*0 | 19807.77889 | 6 | 6 | |
| 1b | 1b | 1b | 1b | 1b | 0 | 0 | 0*0*0*0*0*0*0-1*1*1*1*1*0*0 | 23497.09548 | 5 | 5 | |
| 1b | 1b | 1b | 1b | 0 | 1b | 0 | 0*0*0*0*0*0*0-1*1*1*1*0*1*0 | 24556.31156 | 5 | 5 | |
| 1b | 1b | 1b | 0 | 1b | 1b | 0 | 0*0*0*0*0*0*0-1*1*1*0*1*1*0 | 25503.52764 | 5 | 5 | |
| 1 | 1 | 1 | 1 | 1 | 1 | k | 1*1*1*1*1*1*1-0*0*0*0*0*0*1 | 27214.27136 | 6 | 6+k | |
| 1b | 1b | 1b | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0-1*1*1*1*1*1*1 | 27341.50754 | 7 | 7 | |
| 1b | 1b | 1b | 1b | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*1*1*1*0*0*0 | 30043.60804 | 4 | 4 | |
| 1b | 1b | 1b | 0 | 1b | 0 | 0 | 0*0*0*0*0*0*0-1*1*1*0*1*0*0 | 31501.71859 | 4 | 4 | |
| 1b | 1b | 0 | 1b | 1b | 0 | 0 | 0*0*0*0*0*0*0-1*1*0*1*1*0*0 | 32460.26131 | 4 | 4 | |
| 1b | 1b | 0 | 1b | 0 | 1b | 0 | 0*0*0*0*0*0*0-1*1*0*1*0*1*0 | 33824.73367 | 4 | 4 | |
| 1 | 1 | 1 | 1 | 1 | k | k | 1*1*1*1*1*1*1-0*0*0*0*0*1*1 | 36199.8794 | 5 | 5+2k | |
| 1 | 1 | 1 | 1 | k | 1 | k | 1*1*1*1*1*1*1-0*0*0*0*1*0*1 | 38255.48744 | 5 | 5+2k | |
| 1 | 1 | 1 | k | 1 | 1 | k | 1*1*1*1*1*1*1-0*0*0*1*0*0*1 | 39879.06533 | 5 | 5+2k | |
| 1b | 1b | 1b | 0 | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*1*1*0*0*0*0 | 42226.91457 | 3 | 3 | |
| 1b | 1b | 0 | 1b | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*1*0*1*0*0*0 | 44105.9397 | 3 | 3 | |
| 1b | 1b | 0 | 0 | 1b | 0 | 0 | 0*0*0*0*0*0*0-1*1*0*0*1*0*0 | 45756.46231 | 3 | 3 | |
| 1b | 0 | 1b | 0 | 1b | 0 | 0 | 0*0*0*0*0*0*0-1*0*1*0*1*0*0 | 46829.46734 | 3 | 3 | |
| 1 | 1 | 1 | 1 | k | k | k | 1*1*1*1*1*1*1-0*0*0*0*1*1*1 | 52121.74874 | 4 | 4+3k | |
| 1 | 1 | 1 | k | 1 | k | k | 1*1*1*1*1*1*1-0*0*0*1*0*1*1 | 54487.11558 | 4 | 4+3k | |
| 1 | 1 | k | 1 | 1 | k | k | 1*1*1*1*1*1*1-0*0*1*0*0*1*1 | 57396.0201 | 4 | 4+3k | |
| 1 | 1 | k | 1 | k | 1 | k | 1*1*1*1*1*1*1-0*0*1*0*1*0*1 | 59399.84925 | 4 | 4+3k | |
| 1b | 1b | 0 | 0 | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*1*0*0*0*0*0 | 68840.98492 | 2 | 2 | |
| 1b | 0 | 1b | 0 | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*0*1*0*0*0*0 | 71077.46734 | 2 | 2 | |
| 1b | 0 | 0 | 1b | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*0*0*1*0*0*0 | 73174.44221 | 2 | 2 | |
| 1 | 1 | 1 | k | k | k | k | 1*1*1*1*1*1*1-0*0*0*1*1*1*1 | 78367.59799 | 3 | 3+4k | |
| 1 | 1 | k | 1 | k | k | k | 1*1*1*1*1*1*1-0*0*1*0*1*1*1 | 82986.47236 | 3 | 3+4k | |
| 1 | 1 | k | k | 1 | k | k | 1*1*1*1*1*1*1-0*0*1*1*0*1*1 | 87454.30151 | 3 | 3+4k | |
| 1 | k | 1 | k | 1 | k | k | 1*1*1*1*1*1*1-0*1*0*1*0*1*1 | 89113.82915 | 3 | 3+4k | |
| 1 | 1 | k | k | k | k | k | 1*1*1*1*1*1*1-0*0*1*1*1*1*1 | 131873.7688 | 2 | 2+5k | |
| 1 | k | 1 | k | k | k | k | 1*1*1*1*1*1*1-0*1*0*1*1*1*1 | 137729.3568 | 2 | 2+5k | |
| 1 | k | k | 1 | k | k | k | 1*1*1*1*1*1*1-0*1*1*0*1*1*1 | 141963.3367 | 2 | 2+5k | |
| 1b | 0 | 0 | 0 | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*0*0*0*0*0*0 | 150320.4221 | 1 | 1 | |
| 1 | k | k | k | k | k | k | 1*1*1*1*1*1*1-0*1*1*1*1*1*1 | 290903.9899 | 1 | 1+6k | |

迭代次数与等位点数值差之间的反比关系大体上是成立的,但不够精确,因为差值无法表达数值的分布方式,
| 1 | 1 | 1 | 1 | 1 | k | k | 1*1*1*1*1*1*1-0*0*0*0*0*1*1 | 36199.8794 | 5 | 5+2k | |
| 1 | 1 | 1 | 1 | k | 1 | k | 1*1*1*1*1*1*1-0*0*0*0*1*0*1 | 38255.48744 | 5 | 5+2k | |
| 1 | 1 | 1 | k | 1 | 1 | k | 1*1*1*1*1*1*1-0*0*0*1*0*0*1 | 39879.06533 | 5 | 5+2k |
如这三组数据,5个1的分布方式分别是5,4+1,3+2.同样都是5个1,4+1要比5更为分散,而3+2要比4+1更分散。所以在等位点数值差一致的前提下,数据越分散迭代次数越大。
| 1b | 1b | 1b | 1b | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*1*1*1*0*0*0 | 30043.60804 | 4 | 4 | |
| 1b | 1b | 1b | 0 | 1b | 0 | 0 | 0*0*0*0*0*0*0-1*1*1*0*1*0*0 | 31501.71859 | 4 | 4 | |
| 1b | 1b | 0 | 1b | 1b | 0 | 0 | 0*0*0*0*0*0*0-1*1*0*1*1*0*0 | 32460.26131 | 4 | 4 | |
| 1b | 1b | 0 | 1b | 0 | 1b | 0 | 0*0*0*0*0*0*0-1*1*0*1*0*1*0 | 33824.73367 | 4 | 4 |
同样比较这4组数据,等位点数值差都是4,但分布分别是4,3+1,2+2,2+1+1.按照分散度排序应该是4<3+1<2+2<2+1+1.同样也是数据越分散迭代次数越大。
所以需要找到一个量去描述这种分散度。
因为差值结构的循环节长度为7,因此所谓的分散度只有两种,一种是5-2分散,一种3-4分散。设5-2分散中4+1的分散度为j1,3+2的分散度为j2。设3-4分散中3+1分散度为g1,2+2的分散度为g2,2+1+1的分散度为g3
| k | j1 | j2 | |||||||||||
| -0.6 | -0.3 | -0.5 | |||||||||||
| g1 | g2 | g3 | |||||||||||
| -0.1 | -0.15 | -0.2 | |||||||||||
| 差值结构 | |||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 迭代次数 | 等位点数值差 | 复合等位点数值差 | ||||
| 1b | 1b | 1b | 1b | 1b | 1b | 0 | 0*0*0*0*0*0*0-1*1*1*1*1*1*0 | 19807.77889 | 6 | 6 | 6 | 6 | |
| 1b | 1b | 1b | 1b | 1b | 0 | 0 | 0*0*0*0*0*0*0-1*1*1*1*1*0*0 | 23497.09548 | 5 | 5 | 5 | 5 | |
| 1b | 1b | 1b | 1b | 0 | 1b | 0 | 0*0*0*0*0*0*0-1*1*1*1*0*1*0 | 24556.31156 | 5 | 5 | 5+j1 | 4.7 | |
| 1b | 1b | 1b | 0 | 1b | 1b | 0 | 0*0*0*0*0*0*0-1*1*1*0*1*1*0 | 25503.52764 | 5 | 5 | 5+j2 | 4.5 | |
| 1 | 1 | 1 | 1 | 1 | 1 | k | 1*1*1*1*1*1*1-0*0*0*0*0*0*1 | 27214.27136 | 6 | 6+k | 6+k | 5.4 | |
| 1b | 1b | 1b | 1b | 1b | 1b | 1b | 0*0*0*0*0*0*0-1*1*1*1*1*1*1 | 27341.50754 | 7 | 7 | 7 | 7 | |
| 1b | 1b | 1b | 1b | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*1*1*1*0*0*0 | 30043.60804 | 4 | 4 | 4 | 4 | |
| 1b | 1b | 1b | 0 | 1b | 0 | 0 | 0*0*0*0*0*0*0-1*1*1*0*1*0*0 | 31501.71859 | 4 | 4 | 4+g1 | 3.9 | |
| 1b | 1b | 0 | 1b | 1b | 0 | 0 | 0*0*0*0*0*0*0-1*1*0*1*1*0*0 | 32460.26131 | 4 | 4 | 4+g2 | 3.85 | |
| 1b | 1b | 0 | 1b | 0 | 1b | 0 | 0*0*0*0*0*0*0-1*1*0*1*0*1*0 | 33824.73367 | 4 | 4 | 4+g3 | 3.8 | |
| 1 | 1 | 1 | 1 | 1 | k | k | 1*1*1*1*1*1*1-0*0*0*0*0*1*1 | 36199.8794 | 5 | 5+2k | 5+2k | 3.8 | |
| 1 | 1 | 1 | 1 | k | 1 | k | 1*1*1*1*1*1*1-0*0*0*0*1*0*1 | 38255.48744 | 5 | 5+2k | 5+2k+j1 | 3.5 | |
| 1 | 1 | 1 | k | 1 | 1 | k | 1*1*1*1*1*1*1-0*0*0*1*0*0*1 | 39879.06533 | 5 | 5+2k | 5+2k+j2 | 3.3 | |
| 1b | 1b | 1b | 0 | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*1*1*0*0*0*0 | 42226.91457 | 3 | 3 | 3 | 3 | |
| 1b | 1b | 0 | 1b | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*1*0*1*0*0*0 | 44105.9397 | 3 | 3 | 3+g1 | 2.9 | |
| 1b | 1b | 0 | 0 | 1b | 0 | 0 | 0*0*0*0*0*0*0-1*1*0*0*1*0*0 | 45756.46231 | 3 | 3 | 3+g2 | 2.85 | |
| 1b | 0 | 1b | 0 | 1b | 0 | 0 | 0*0*0*0*0*0*0-1*0*1*0*1*0*0 | 46829.46734 | 3 | 3 | 3+g3 | 2.8 | |
| 1 | 1 | 1 | 1 | k | k | k | 1*1*1*1*1*1*1-0*0*0*0*1*1*1 | 52121.74874 | 4 | 4+3k | 4+3k | 2.2 | |
| 1 | 1 | 1 | k | 1 | k | k | 1*1*1*1*1*1*1-0*0*0*1*0*1*1 | 54487.11558 | 4 | 4+3k | 4+3k+g1 | 2.1 | |
| 1 | 1 | k | 1 | 1 | k | k | 1*1*1*1*1*1*1-0*0*1*0*0*1*1 | 57396.0201 | 4 | 4+3k | 4+3k+g2 | 2.05 | |
| 1 | 1 | k | 1 | k | 1 | k | 1*1*1*1*1*1*1-0*0*1*0*1*0*1 | 59399.84925 | 4 | 4+3k | 4+3k+g3 | 2 | |
| 1b | 1b | 0 | 0 | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*1*0*0*0*0*0 | 68840.98492 | 2 | 2 | 2 | 2 | |
| 1b | 0 | 1b | 0 | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*0*1*0*0*0*0 | 71077.46734 | 2 | 2 | 2+j1 | 1.7 | |
| 1b | 0 | 0 | 1b | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*0*0*1*0*0*0 | 73174.44221 | 2 | 2 | 2+j2 | 1.5 | |
| 1 | 1 | 1 | k | k | k | k | 1*1*1*1*1*1*1-0*0*0*1*1*1*1 | 78367.59799 | 3 | 3+4k | 3+4k | 0.6 | |
| 1 | 1 | k | 1 | k | k | k | 1*1*1*1*1*1*1-0*0*1*0*1*1*1 | 82986.47236 | 3 | 3+4k | 3+4k+g1 | 0.5 | |
| 1 | 1 | k | k | 1 | k | k | 1*1*1*1*1*1*1-0*0*1*1*0*1*1 | 87454.30151 | 3 | 3+4k | 3+4k+g2 | 0.45 | |
| 1 | k | 1 | k | 1 | k | k | 1*1*1*1*1*1*1-0*1*0*1*0*1*1 | 89113.82915 | 3 | 3+4k | 3+4k+g3 | 0.4 | |
| 1 | 1 | k | k | k | k | k | 1*1*1*1*1*1*1-0*0*1*1*1*1*1 | 131873.7688 | 2 | 2+5k | 2+5k | -1 | |
| 1 | k | 1 | k | k | k | k | 1*1*1*1*1*1*1-0*1*0*1*1*1*1 | 137729.3568 | 2 | 2+5k | 2+5k+j1 | -1.3 | |
| 1 | k | k | 1 | k | k | k | 1*1*1*1*1*1*1-0*1*1*0*1*1*1 | 141963.3367 | 2 | 2+5k | 2+5k+j2 | -1.5 | |
| 1b | 0 | 0 | 0 | 0 | 0 | 0 | 0*0*0*0*0*0*0-1*0*0*0*0*0*0 | 150320.4221 | 1 | 1 | 1 | 1 | |
| 1 | k | k | k | k | k | k | 1*1*1*1*1*1*1-0*1*1*1*1*1*1 | 290903.9899 | 1 | 1+6k | 1+6k | -2.6 | |
得到复合的等位点数值差,只要且当的设置k,j1,j2,g1,g2,g3的值就可以相对理想的拟合迭代次数与等位点数值差的反比关系。如设k=-0.6,j1=-0.3,j2=-0.5,g1=-0.1,g2=-0.15,g3=-0.2
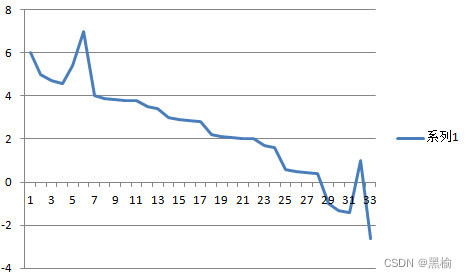
这组数据也体现了数据分布的散度的绝对值与迭代次数的正比关系。