自动梯度计算

news2024/9/23 13:21:41

神经网络的参数主要通过梯度下降来进行优化．当确定了风险函数以及网络结构后，我们就可以手动用链式法则来计算风险函数对每个参数的梯度，并用代码进行实现．但是手动求导并转换为计算机程序的过程非常琐碎并容易出错，导致实现神经网络变得十分低效．实际上，参数的梯度可以让计算机来自动计算．目前，主流的深度学习框架都包含了自动梯度计算的功能，即我们可以只考虑网络结构并用代码实现，其梯度可以自动进行计算，无须人工干预，这样可以大幅提高开发效率．
自动计算梯度的方法可以分为以下三类：数值微分、符号微分和自动微分．

1. 数值微分

数值微分（ Numerical Differentiation）是用数值方法来计算函数𝑓(𝑥)的导数．函数𝑓(𝑥)的点𝑥 的导数定义为

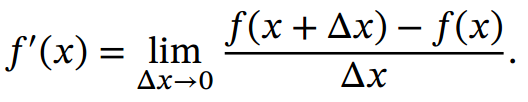
要计算函数 𝑓(𝑥) 在点 𝑥 的导数，可以对 𝑥 加上一个很少的非零的扰动 Δ𝑥，通过上述定义来直接计算函数𝑓(𝑥)的梯度．数值微分方法非常容易实现，但找到一个合适的扰动 Δ𝑥 却十分困难．如果 Δ𝑥 过小，会引起数值计算问题，比如舍入误差；如果Δ𝑥 过大，会增加截断误差，使得导数计算不准确．因此，数值微分的实用性比较差．

在实际应用，经常使用下面公式来计算梯度，可以减少截断误差．

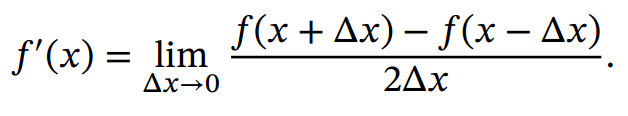
数值微分的另外一个问题是计算复杂度．假设参数数量为𝑁，则每个参数都需要单独施加扰动，并计算梯度．假设每次正向传播的计算复杂度为𝑂(𝑁)，则计算数值微分的总体时间复杂度为 $O(N^2)$ ．

2. 符号微分

符号微分（ Symbolic Differentiation）是一种基于符号计算的自动求导方法．符号计算也叫代数计算，是指用计算机来处理带有变量的数学表达式．这里的变量被看作符号（ Symbols），一般不需要代入具体的值．符号计算的输入和输出都是数学表达式，一般包括对数学表达式的化简、因式分解、微分、积分、解代数方程、求解常微分方程等运算．

比如数学表达式的化简：

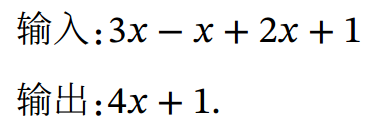
符号计算一般来讲是对输入的表达式，通过迭代或递归使用一些事先定义的规则进行转换．当转换结果不能再继续使用变换规则时，便停止计算．
符号微分可以在编译时就计算梯度的数学表示，并进一步利用符号计算方法进行优化．此外，符号计算的一个优点是符号计算和平台无关，可以在CPU或GPU 上运行．符号微分也有一些不足之处： 1）编译时间较长，特别是对于循环，需要很长时间进行编译； 2）为了进行符号微分，一般需要设计一种专门的语言来表示数学表达式，并且要对变量（符号）进行预先声明； 3）很难对程序进行调试．

3. 自动微分

自动微分（ Automatic Differentiation， AD）是一种可以对一个（程序）函数进行计算导数的方法．符号微分的处理对象是数学表达式，而自动微分的处理对象是一个函数或一段程序．

自动微分的基本原理是所有的数值计算可以分解为一些基本操作，包含+, −, ×, / 和一些初等函数 exp, log, sin, cos 等，然后利用链式法则来自动计算一个复合函数的梯度．

为简单起见，这里以一个神经网络中常见的复合函数的例子来说明自动微分的过程．令复合函数𝑓(𝑥; 𝑤, 𝑏)为

其中𝑥 为输入标量， 𝑤 和𝑏分别为权重和偏置参数．

首先，我们将复合函数 𝑓(𝑥; 𝑤, 𝑏) 分解为一系列的基本操作，并构成一个计算图（ Computational Graph）．计算图是数学运算的图形化表示．计算图中的每个非叶子节点表示一个基本操作，每个叶子节点为一个输入变量或常量．下图给出了当 𝑥 = 1, 𝑤 = 0, 𝑏 = 0 时复合函数 𝑓(𝑥; 𝑤, 𝑏) 的计算图，其中连边上的红色数字表示前向计算时复合函数中每个变量的实际取值．

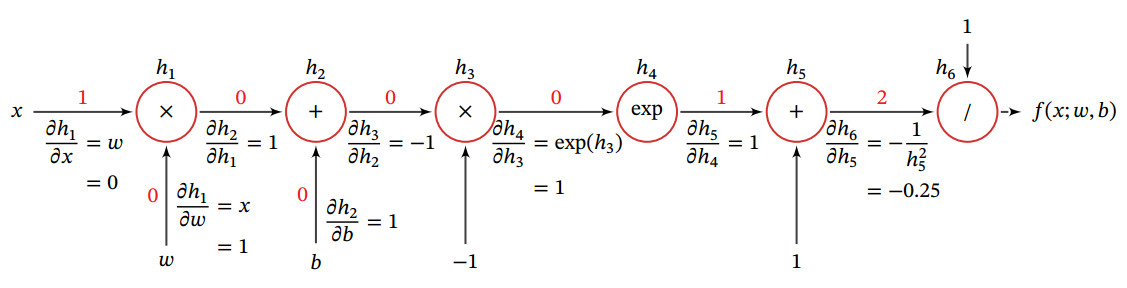
从计算图上可以看出，复合函数 𝑓(𝑥; 𝑤, 𝑏) 由 6 个基本函数 ℎ𝑖, 1 ≤ 𝑖 ≤ 6 组成．如下表所示，每个基本函数的导数都十分简单，可以通过规则来实现．

整个复合函数 𝑓(𝑥; 𝑤, 𝑏) 关于参数 𝑤 和 𝑏 的导数可以通过计算图上的节点𝑓(𝑥; 𝑤, 𝑏)与参数𝑤 和𝑏之间路径上所有的导数连乘来得到，即

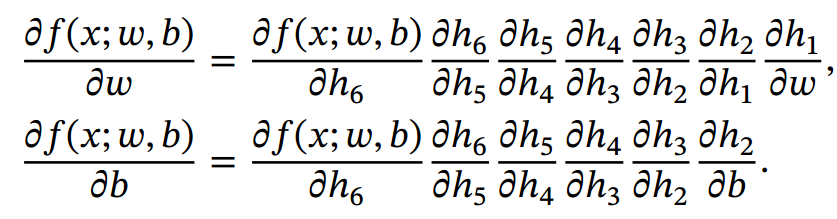
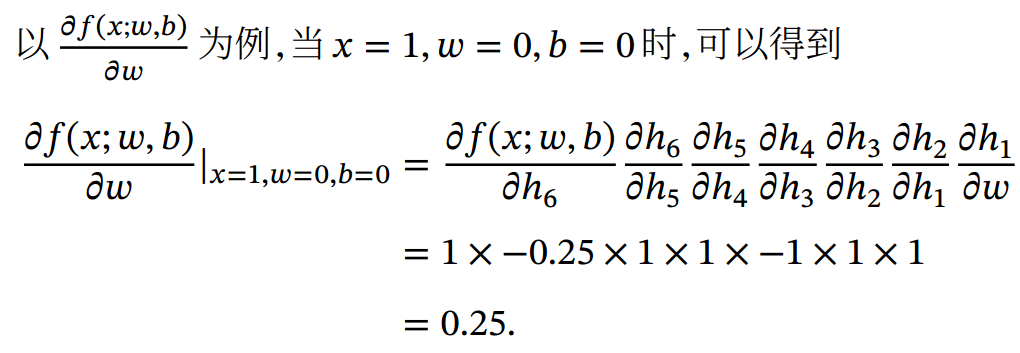
如果函数和参数之间有多条路径，可以将这多条路径上的导数再进行相加，得到最终的梯度．

按照计算导数的顺序，自动微分可以分为两种模式：前向模式和反向模式．

3.1. 前向模式

前向模式是按计算图中计算方向的相同方向来递归地计算梯度．以 $\frac{\partial f(x;w, b)}{\partial b}$ 为例，当𝑥 = 1, 𝑤 = 0, 𝑏 = 0时，前向模式的累积计算顺序如下：

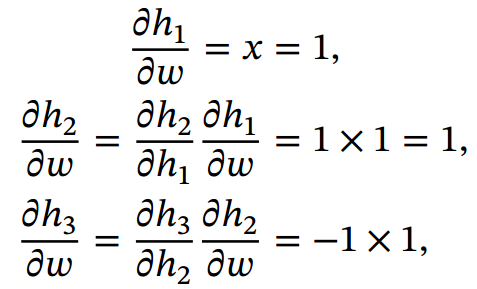
3.2. 反向模式

反向模式是按计算图中计算方向的相反方向来递归地计算梯度．以 $\frac{\partial f(x;w, b)}{\partial b}$ 为例，当𝑥 = 1, 𝑤 = 0, 𝑏 = 0时，反向模式的累积计算顺序如下：

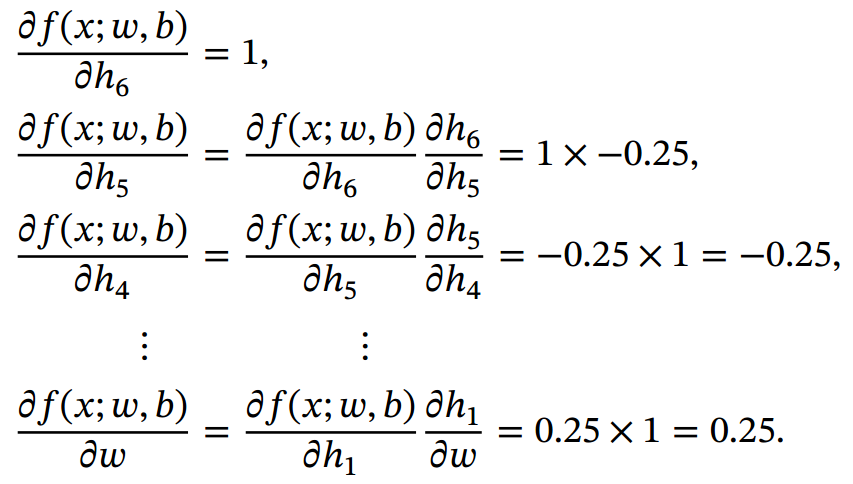
前向模式和反向模式可以看作应用链式法则的两种梯度累积方式．从反向模式的计算顺序可以看出，反向模式和反向传播的计算梯度的方式相同．

对于一般的函数形式 $f: R^N \rightarrow R^M$ ，前向模式需要对每一个输入变量都进行一遍遍历，共需要 𝑁 遍．而反向模式需要对每一个输出都进行一个遍历，共需要𝑀 遍．当𝑁 > 𝑀 时，反向模式更高效．在前馈神经网络的参数学习中，风险函数为 $f: R^N \rightarrow R$ ，输出为标量，因此采用反向模式为最有效的计算方式，只需要一遍计算．

3.3. 静态计算图和动态计算图

计算图按构建方式可以分为静态计算图（ Static Computational Graph）和动态计算图（ Dynamic Computational Graph）．静态计算图是在编译时构建计算图，计算图构建好之后在程序运行时不能改变，而动态计算图是在程序运行时动态构建．两种构建方式各有优缺点．静态计算图在构建时可以进行优化，并行能力强，但灵活性比较差．动态计算图则不容易优化，当不同输入的网络结构不一致时，难以并行计算，但是灵活性比较高．

3.4. 符号微分和自动微分

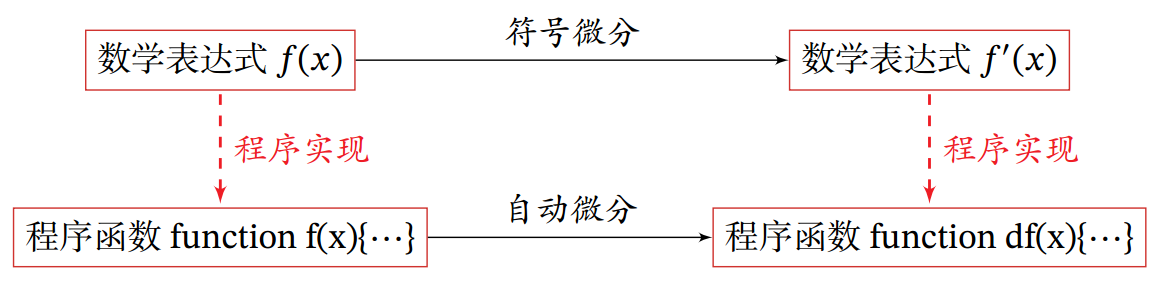
符号微分和自动微分都利用计算图和链式法则来自动求解导数．符号微分在编译阶段先构造一个复合函数的计算图，通过符号计算得到导数的表达式，还可以对导数表达式进行优化，在程序运行阶段才代入变量的具体数值来计算导数．而自动微分则无须事先编译，在程序运行阶段边计算边记录计算图，计算图上的局部梯度都直接代入数值进行计算，然后用前向或反向模式来计算最终的梯度．

下图给出了符号微分与自动微分的对比．