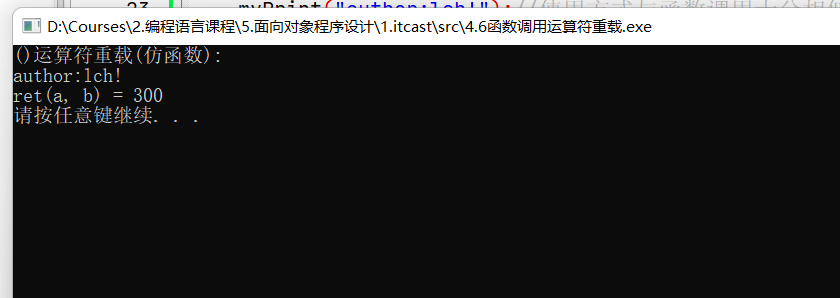
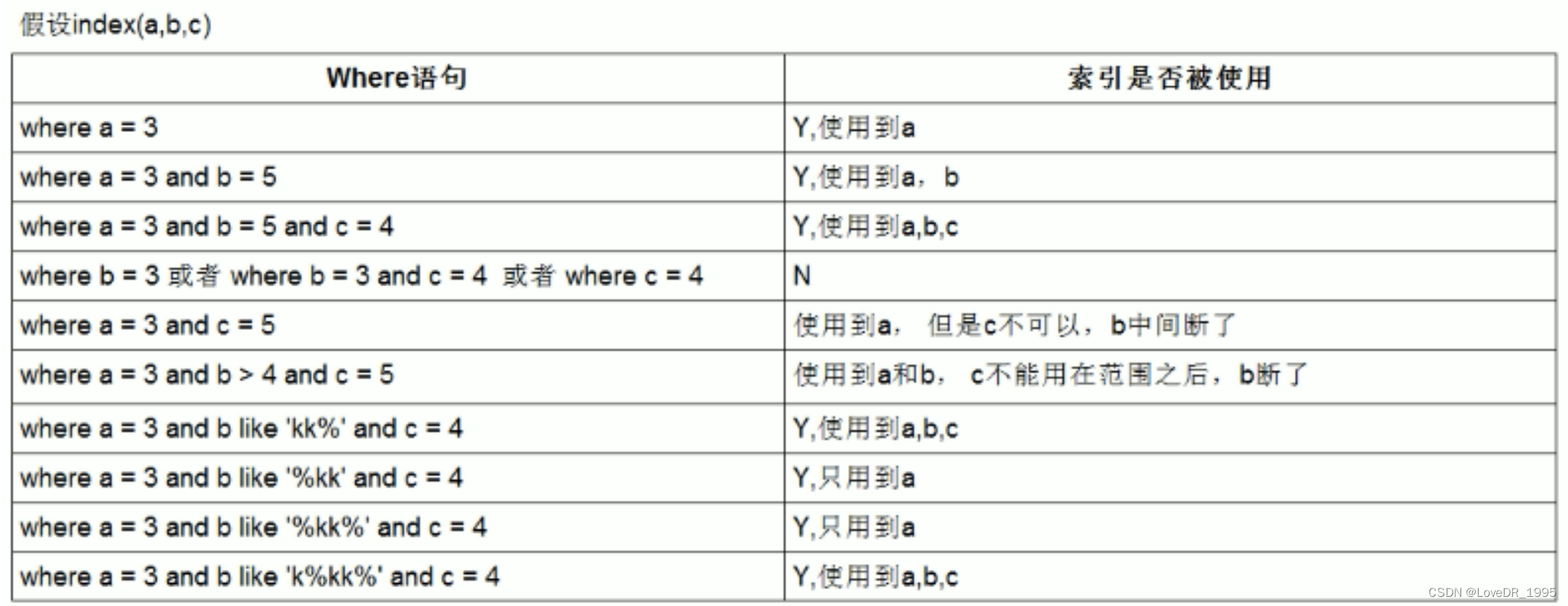
目录
- 第一天
- 第二章:简单的神经网络
- 第三章:深度学习工作流程
- 卷积模块介绍
- 卷积
- 池化层
- 池化层书中的代码
- 池化层相关资料
- 提取 (各)层(的)结构
- 如何提取参数及自定义初始化
- LeNet
- AlexNet
- VGGNet
- CIFAR 10
- VGGNet
- GoogLeNet
- Inception 模块
- ResNet
- 案例-MNIST手写数字分类
- 实现cifar10分类
- 图像增强
- 定义基本模块
第一天
官网:PyTorch
Markdown语法:markdown_百度百科 (baidu.com)
第二章:简单的神经网络
英文概念
如果要手动设计神经网络,则
权重矩阵的大小为input_size x hidden_size,
这会将您输入的大小input_size转换为大小hidden_size。
epoch是通过网络进行迭代的计数器值。
epoch的概念最终取决于程序员如何定义迭代过程。
通常,对于每个周期,您都要遍历整个数据集,然后对每个周期重复一次。
汉语概念:
学习率决定了我们希望我们的网络从每次迭代的误差中获取反馈的速度。
它通过忘记网络从所有先前迭代中学到的知识来决定从当前迭代中学到的知识。
将学习率保持为 1 可使网络考虑完全误差,并根据完全误差调整权重。 学习率为 0 意味着向网络传递的信息为零。
学习率将是神经网络中梯度更新方程式中的选择因子。
较低的学习率可帮助网络沿着山路走很小的步,而较高的学习率可帮助网络沿山路走。 但是,这是有代价的。 一旦损失接近最小值,较高的学习率可能会使网络跳过最小值,并导致网络永远找不到最小值。 从技术上讲,在每次迭代中,网络都会对近似值进行线性近似,而学习率将控制该近似值。
如果损失函数高度弯曲,则以较高的学习率进行较长的步骤可能会导致模型变坏。 因此,理想的学习率始终取决于问题陈述和当前的模型架构
我们将为各种神经网络模型定义五个典型的超参数:
epochs = 500
batches = 64
lr = 0.01
input_size = 10
output_size = 4
hidden_size = 100
我们需要在程序顶部定义输入和输出大小,这将帮助我们在不同的地方使用输入和输出大小,例如网络设计函数。
隐藏大小是隐藏层中神经元的数量。
对于每个神经元,我们运行以下公式来更新神经元的权重:
weight -= lr * loss
张量充当计算图中的一个节点,并通过函数式模块实例连接到其他节点。 张量实例主要具有支持 Autograd 的三个属性:.grad,.data和grad_fn()(注意字母大小写:Function代表 PyTorch Function模块,而function代表 Python 函数)。
.grad属性在任何时间点存储梯度,所有向后调用将当前梯度累积到.grad属性。 .data属性可访问其中包含数据的裸张量对象。
backward() - 知乎 (zhihu.com)
线性层也称为全连接层或密集层,它在权重和输入之间进行矩阵乘法。
Parameter类将权重和偏差添加到模块参数列表中
apply()此函数可帮助我们将自定义函数应用于模型的所有参数,它通常用于进行自定义权重初始化。
net = FizBuzNet(input_size, hidden_size, output_size) net.cpu() # convert all parameters to CPU tensors net.cuda() # convert all parameters to GPU tensors`
nn.Module附带的一个重要层是顺序容器,如果模型的结构是连续且直接的,则它提供了一个易于使用的 API 来制作模型对象而无需用户编写类结构。
人们已经提出了更好的解决方案,例如 ReLU,Leaky ReLU 和 ELU。
第三章:深度学习工作流程
transforms模块为常用的预处理函数(例如填充,裁切,灰度缩放,仿射变换,将图像转换为 PyTorch 张量等)提供了开箱即用的实现,以及一些实现数据扩充,例如翻转,随机裁剪和色彩抖动。
Compose工具将多个转换组合在一起,以形成一个管道对象。
ToTensor将三通道输入 RGB 图像转换为尺寸为通道×宽度×高度的三维张量。 这是 PyTorch 中视觉网络期望的尺寸顺序。
在这里插入代码片
卷积模块介绍
卷积网络在计算机视觉领域被应用得非常广泛,那么常见的卷机网络中用到的模块能够使用 pytorch 非常轻松地实现,下面我们来讲一下 pytorch 中的卷积模块

卷积
卷积(块)在 pytorch 中有两种方式,一种是 torch.nn.Conv2d(),一种是 torch.nn.functional.conv2d(),这两种形式本质都是使用一个卷积操作
这两种形式的卷积对于输入的要求都是一样的,首先需要输入是一个 torch.autograd.Variable() 的类型,大小是 (batch, channel, H, W),其中 batch 表示输入的一批数据的数目,第二个是输入的通道数,一般一张彩色的图片是 3,灰度图是 1,而卷积网络过程中的通道数比较大,会出现几十到几百的通道数,H 和 W 表示输入图片的高度和宽度,比如一个 batch 是 32 张图片,每张图片是 3 通道,高和宽分别是 50 和 100,那么输入的大小就是 (32, 3, 50, 100)
下面举例来说明一下这两种卷积方式
import numpy as np
import torch
from torch import nn
from torch.autograd import Variable
import torch.nn.functional as F
from PIL import Image
import matplotlib.pyplot as plt
%matplotlib inline
im = Image.open('./cat.png').convert('L') # 读入一张灰度图的图片
im = np.array(im, dtype='float32') # 将其转换为一个矩阵
# 可视化图片
plt.imshow(im.astype('uint8'), cmap='gray')
<matplotlib.image.AxesImage at 0x108634c88>
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8x1XcVJx-1672562670014)(output_4_1.png)]](https://img-blog.csdnimg.cn/3617a54e276e4831a6b7ae3d1e034f5e.png)
# 将图片矩阵转化为 pytorch tensor,并适配卷积输入的要求
im = torch.from_numpy(im.reshape((1, 1, im.shape[0], im.shape[1])))
下面我们定义一个算子对其进行轮廓检测
# 使用 nn.Conv2d
conv1 = nn.Conv2d(1, 1, 3, bias=False) # 定义卷积
sobel_kernel = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]], dtype='float32') # 定义轮廓检测算子
sobel_kernel = sobel_kernel.reshape((1, 1, 3, 3)) # 适配卷积的输入输出
conv1.weight.data = torch.from_numpy(sobel_kernel) # 给卷积的 kernel 赋值
edge1 = conv1(Variable(im)) # 作用在图片上
edge1 = edge1.data.squeeze().numpy() # 将输出转换为图片的格式
下面我们可视化边缘检测之后的结果
plt.imshow(edge1, cmap='gray')
<matplotlib.image.AxesImage at 0x109a4a128>
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9RwvM7kI-1672562670015)(output_9_1.png)]](https://img-blog.csdnimg.cn/83c95158b17d4d46acfe77d2f20bdb8a.png)
# 使用 F.conv2d
sobel_kernel = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]], dtype='float32') # 定义轮廓检测算子
sobel_kernel = sobel_kernel.reshape((1, 1, 3, 3)) # 适配卷积的输入输出
weight = Variable(torch.from_numpy(sobel_kernel))
edge2 = F.conv2d(Variable(im), weight) # 作用在图片上
edge2 = edge2.data.squeeze().numpy() # 将输出转换为图片的格式
plt.imshow(edge2, cmap='gray')
详解pytorch中squeeze()和unsqueeze()函数介绍
<matplotlib.image.AxesImage at 0x10a103eb8>
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-w0eg4pVi-1672562670015)(output_10_1.png)]](https://img-blog.csdnimg.cn/5a776b897cfb4b2fb186ce11e3e5d80f.png)
可以看到两种形式能够得到相同的效果,不同的地方相信你也看到了,使用 nn.Conv2d() 相当于直接定义了一层卷积网络结构,而使用 torch.nn.functional.conv2d() 相当于定义了一个卷积的操作,所以使用后者需要再额外去定义一个 weight,而且这个 weight 也必须是一个 Variable,而使用 nn.Conv2d() 则会帮我们默认定义一个随机初始化的 weight,如果我们需要修改,那么取出其中的值对其修改,如果不想修改,那么可以直接使用这个默认初始化的值,非常方便
实际使用中我们基本都使用 nn.Conv2d() 这种形式
池化层
卷积网络中另外一个非常重要的结构就是池化,这是利用了图片的下采样不变性,即一张图片变小了还是能够看出了这张图片的内容,而使用池化层能够将图片大小降低,非常好地提高了计算效率,同时池化层也没有参数。池化的方式有很多种,比如最大值池化,均值池化等等,在卷积网络中一般使用最大值池化。
在 pytorch 中最大值池化的方式也有两种,一种是 nn.MaxPool2d(),一种是 torch.nn.functional.max_pool2d(),他们对于图片的输入要求跟卷积对于图片的输入要求是一样了,就不再赘述,下面我们也举例说明
# 使用 nn.MaxPool2d
pool1 = nn.MaxPool2d(2, 2)
print('before max pool, image shape: {} x {}'.format(im.shape[2], im.shape[3]))
small_im1 = pool1(Variable(im))
small_im1 = small_im1.data.squeeze().numpy()
print('after max pool, image shape: {} x {} '.format(small_im1.shape[0], small_im1.shape[1]))
before max pool, image shape: 224 x 224
after max pool, image shape: 112 x 112
可以看到图片的大小减小了一半,那么图片是不是变了呢?我们可以可视化一下
plt.imshow(small_im1, cmap='gray')
<matplotlib.image.AxesImage at 0x10a5867f0>
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OJWAjtQo-1672562670016)(output_15_1.png)]](https://img-blog.csdnimg.cn/b20dae79e2bb42a3afbdb408f09d208d.png)
可以看到图片几乎没有变化,说明池化层只是减小了图片的尺寸,并不会影响图片的内容
# F.max_pool2d
print('before max pool, image shape: {} x {}'.format(im.shape[2], im.shape[3]))
small_im2 = F.max_pool2d(Variable(im), 2, 2)
small_im2 = small_im2.data.squeeze().numpy()
print('after max pool, image shape: {} x {} '.format(small_im1.shape[0], small_im1.shape[1]))
plt.imshow(small_im2, cmap='gray')
before max pool, image shape: 224 x 224
after max pool, image shape: 112 x 112
<matplotlib.image.AxesImage at 0x10a6ac898>
![(img-vtnSndp1-1672562670016)(output_17_2.png)]](https://img-blog.csdnimg.cn/98dc198c720f49d88bf4bdbd5f9c2580.png)
跟卷积层一样,实际使用中,我们一般使用 nn.MaxPool2d()
池化层书中的代码

可以看到,大多用了add_module()函数。


目前的model()只是卷积层、激活层、池化层的三合一。
下面是作者的建议,个人感觉很有用。

池化层相关资料
pytorch中的add_module函数
【Pytorch学习】add_module()函数用法
提取 (各)层(的)结构
对于一个给定的模型,如果不想要模型中所有的层结构,只希望能够提取网络中的某一层或者几层,应该如何来实现呢?

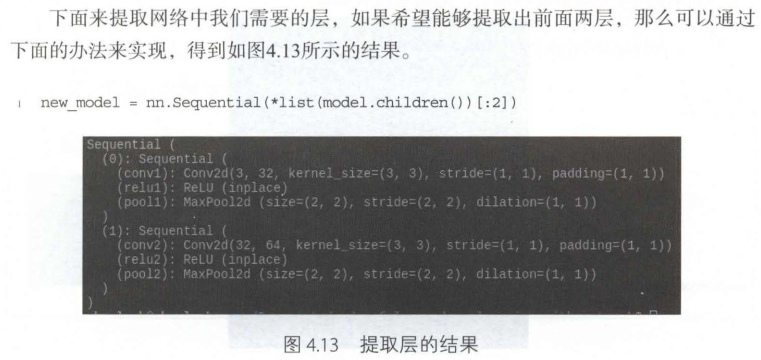

如何提取参数及自定义初始化
有时候提取出的层结构并不够,还需要对里面的参数进行初始化,那么如何提取出网络的参数并对其初始化呢?


如何对权重做初始化呢?非常简单,因为权重是一个 Variable,所以只需要取出其中的data 属性,然后对它进行所需要的处理就可以了。
下面是模板性的代码:

通过上面的操作,对将卷积层中使用PyTorch里面提供的方法的权重进行初始化,
这样就能够使用任意我们想使用的初始化,
甚至我们可以自己定义初始化方法并对权重进行初始化。
一整个流程的操作出了看上文,还可以看这个博文:https://blog.csdn.net/weixin_41560402/article/details/108122910
至于自定义怎么弄,如果日后我弄项目的时候遇到了这块知识,我会进行补充的。
pytorch参数初始化方法
Pytorch参数初始化–默认与自定义
【pytorch参数初始化】 pytorch默认参数初始化以及自定义参数初始化
LeNet



这样就实现了LeNet网络,可以发现网络的层数很浅,也没有添加激活层。
AlexNet
AlexNet网络相对于LeNet,层数更深,同时第一次引入了激活层ReLU,在全连接层引入了DropOut层防止过拟合。



VGGNet


它之所以使用很多小的滤波器,是因为
- 层叠很多小的滤波器的感受野和一个大的滤波器的感受野是相同的,
- 还能减少参数,
- 同时有更深的网络结构。




其实可以看出VGG只是对网络层进行不断的堆叠,并没有进行太多的创新,而增加深度确实可以一定程度改善模型效果。
计算机视觉是一直深度学习的主战场,从这里我们将接触到近几年非常流行的卷积网络结构,网络结构由浅变深,参数越来越多,网络有着更多的跨层链接,首先我们先介绍一个数据集 cifar10,我们将以此数据集为例介绍各种卷积网络的结构。
CIFAR 10
cifar 10 这个数据集一共有 50000 张训练集,10000 张测试集,两个数据集里面的图片都是 png 彩色图片,图片大小是 32 x 32 x 3,一共是 10 分类问题,分别为飞机、汽车、鸟、猫、鹿、狗、青蛙、马、船和卡车。这个数据集是对网络性能测试一个非常重要的指标,可以说如果一个网络在这个数据集上超过另外一个网络,那么这个网络性能上一定要比另外一个网络好,目前这个数据集最好的结果是 95% 左右的测试集准确率。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AjpnTuAc-1672578260381)(null)]
你能用肉眼对这些图片进行分类吗?
cifar 10 已经被 pytorch 内置了,使用非常方便,只需要调用 torchvision.datasets.CIFAR10 就可以了
VGGNet
vggNet 是第一个真正意义上的深层网络结构,其是 ImageNet2014年的冠军,得益于 python 的函数和循环,我们能够非常方便地构建重复结构的深层网络。
vgg 的网络结构非常简单,就是不断地堆叠卷积层和池化层,下面是一个简单的图示
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KD8lL98K-1672578260426)(null)]
vgg 几乎全部使用 3 x 3 的卷积核以及 2 x 2 的池化层,使用小的卷积核进行多层的堆叠和一个大的卷积核的感受野是相同的,同时小的卷积核还能减少参数,同时可以有更深的结构。
vgg 的一个关键就是使用很多层 3 x 3 的卷积然后再使用一个最大池化层,这个模块被使用了很多次,下面我们照着这个结构来写一写
import sys
sys.path.append('..')
import numpy as np
import torch
from torch import nn
from torch.autograd import Variable
from torchvision.datasets import CIFAR10
我们可以定义一个 vgg 的 block,传入三个参数,第一个是模型层数,第二个是输入的通道数,第三个是输出的通道数,第一层卷积接受的输入通道就是图片输入的通道数,然后输出最后的输出通道数,后面的卷积接受的通道数就是最后的输出通道数
def vgg_block(num_convs, in_channels, out_channels):
net = [nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1), nn.ReLU(True)] # 定义第一层
for i in range(num_convs-1): # 定义后面的很多层
net.append(nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1))
net.append(nn.ReLU(True))
net.append(nn.MaxPool2d(2, 2)) # 定义池化层
return nn.Sequential(*net)
我们可以将模型打印出来看看结构
block_demo = vgg_block(3, 64, 128)
print(block_demo)
Sequential(
(0): Conv2d (64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace)
(2): Conv2d (128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(3): ReLU(inplace)
(4): Conv2d (128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(5): ReLU(inplace)
(6): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), dilation=(1, 1))
)
# 首先定义输入为 (1, 64, 300, 300)
input_demo = Variable(torch.zeros(1, 64, 300, 300))
output_demo = block_demo(input_demo)
print(output_demo.shape)
torch.Size([1, 128, 150, 150])
可以看到输出就变为了 (1, 128, 150, 150),可以看到经过了这一个 vgg block,输入大小被减半,通道数变成了 128
下面我们定义一个函数对这个 vgg block 进行堆叠
def vgg_stack(num_convs, channels):
net = []
for n, c in zip(num_convs, channels):
in_c = c[0]
out_c = c[1]
net.append(vgg_block(n, in_c, out_c))
return nn.Sequential(*net)
作为实例,我们定义一个稍微简单一点的 vgg 结构,其中有 8 个卷积层
vgg_net = vgg_stack((1, 1, 2, 2, 2), ((3, 64), (64, 128), (128, 256), (256, 512), (512, 512)))
print(vgg_net)
Sequential(
(0): Sequential(
(0): Conv2d (3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace)
(2): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), dilation=(1, 1))
)
(1): Sequential(
(0): Conv2d (64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace)
(2): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), dilation=(1, 1))
)
(2): Sequential(
(0): Conv2d (128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace)
(2): Conv2d (256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(3): ReLU(inplace)
(4): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), dilation=(1, 1))
)
(3): Sequential(
(0): Conv2d (256, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace)
(2): Conv2d (512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(3): ReLU(inplace)
(4): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), dilation=(1, 1))
)
(4): Sequential(
(0): Conv2d (512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace)
(2): Conv2d (512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(3): ReLU(inplace)
(4): MaxPool2d(kernel_size=(2, 2), stride=(2, 2), dilation=(1, 1))
)
)
我们可以看到网络结构中有个 5 个 最大池化,说明图片的大小会减少 5 倍,我们可以验证一下,输入一张 256 x 256 的图片看看结果是什么
test_x = Variable(torch.zeros(1, 3, 256, 256))
test_y = vgg_net(test_x)
print(test_y.shape)
torch.Size([1, 512, 8, 8])
可以看到图片减小了 2 5 2^5 25 倍,最后再加上几层全连接,就能够得到我们想要的分类输出
class vgg(nn.Module):
def __init__(self):
super(vgg, self).__init__()
self.feature = vgg_net
self.fc = nn.Sequential(
nn.Linear(512, 100),
nn.ReLU(True),
nn.Linear(100, 10)
)
def forward(self, x):
x = self.feature(x)
x = x.view(x.shape[0], -1)
x = self.fc(x)
return x
然后我们可以训练我们的模型看看在 cifar10 上的效果
from utils import train
def data_tf(x):
x = np.array(x, dtype='float32') / 255
x = (x - 0.5) / 0.5 # 标准化,这个技巧之后会讲到
x = x.transpose((2, 0, 1)) # 将 channel 放到第一维,只是 pytorch 要求的输入方式
x = torch.from_numpy(x)
return x
train_set = CIFAR10('./data', train=True, transform=data_tf)
train_data = torch.utils.data.DataLoader(train_set, batch_size=64, shuffle=True)
test_set = CIFAR10('./data', train=False, transform=data_tf)
test_data = torch.utils.data.DataLoader(test_set, batch_size=128, shuffle=False)
net = vgg()
optimizer = torch.optim.SGD(net.parameters(), lr=1e-1)
criterion = nn.CrossEntropyLoss()
train(net, train_data, test_data, 20, optimizer, criterion)
Epoch 0. Train Loss: 2.303118, Train Acc: 0.098186, Valid Loss: 2.302944, Valid Acc: 0.099585, Time 00:00:32
Epoch 1. Train Loss: 2.303085, Train Acc: 0.096907, Valid Loss: 2.302762, Valid Acc: 0.100969, Time 00:00:33
Epoch 2. Train Loss: 2.302916, Train Acc: 0.097287, Valid Loss: 2.302740, Valid Acc: 0.099585, Time 00:00:33
Epoch 3. Train Loss: 2.302395, Train Acc: 0.102042, Valid Loss: 2.297652, Valid Acc: 0.108782, Time 00:00:32
Epoch 4. Train Loss: 2.079523, Train Acc: 0.202026, Valid Loss: 1.868179, Valid Acc: 0.255736, Time 00:00:31
Epoch 5. Train Loss: 1.781262, Train Acc: 0.307625, Valid Loss: 1.735122, Valid Acc: 0.323279, Time 00:00:31
Epoch 6. Train Loss: 1.565095, Train Acc: 0.400975, Valid Loss: 1.463914, Valid Acc: 0.449565, Time 00:00:31
Epoch 7. Train Loss: 1.360450, Train Acc: 0.495225, Valid Loss: 1.374488, Valid Acc: 0.490803, Time 00:00:31
Epoch 8. Train Loss: 1.144470, Train Acc: 0.585758, Valid Loss: 1.384803, Valid Acc: 0.524624, Time 00:00:31
Epoch 9. Train Loss: 0.954556, Train Acc: 0.659287, Valid Loss: 1.113850, Valid Acc: 0.609968, Time 00:00:32
Epoch 10. Train Loss: 0.801952, Train Acc: 0.718131, Valid Loss: 1.080254, Valid Acc: 0.639933, Time 00:00:31
Epoch 11. Train Loss: 0.665018, Train Acc: 0.765945, Valid Loss: 0.916277, Valid Acc: 0.698972, Time 00:00:31
Epoch 12. Train Loss: 0.547411, Train Acc: 0.811241, Valid Loss: 1.030948, Valid Acc: 0.678896, Time 00:00:32
Epoch 13. Train Loss: 0.442779, Train Acc: 0.846228, Valid Loss: 0.869791, Valid Acc: 0.732496, Time 00:00:32
Epoch 14. Train Loss: 0.357279, Train Acc: 0.875440, Valid Loss: 1.233777, Valid Acc: 0.671677, Time 00:00:31
Epoch 15. Train Loss: 0.285171, Train Acc: 0.900096, Valid Loss: 0.852879, Valid Acc: 0.765131, Time 00:00:32
Epoch 16. Train Loss: 0.222431, Train Acc: 0.923374, Valid Loss: 1.848096, Valid Acc: 0.614023, Time 00:00:31
Epoch 17. Train Loss: 0.174834, Train Acc: 0.939478, Valid Loss: 1.137286, Valid Acc: 0.728639, Time 00:00:31
Epoch 18. Train Loss: 0.144375, Train Acc: 0.950587, Valid Loss: 0.907310, Valid Acc: 0.776800, Time 00:00:31
Epoch 19. Train Loss: 0.115332, Train Acc: 0.960878, Valid Loss: 1.009886, Valid Acc: 0.761175, Time 00:00:31
可以看到,跑完 20 次,vgg 能在 cifar 10 上取得 76% 左右的测试准确率
GoogLeNet
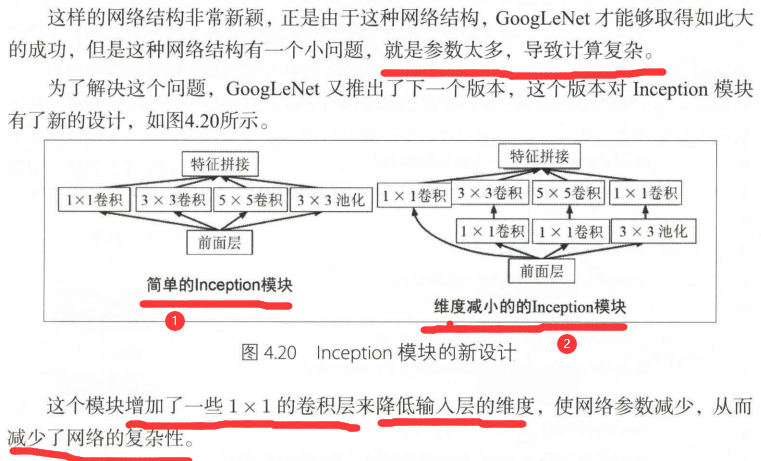
GoogLeNet也叫InceptionNet,是在2014年被提出的,如今已经进化到了v4版本,
下面介绍它最核心的部分。
GoogLeNet采取了比VGGNet更深的网络结构,一共有22层,但是它的参数却比AlexNet少了12 倍,同时有很高的计算效率,因为它采用了一种
很有效的Inception模块,而且它也没有全连接层,
是2014年比赛的冠军。
深度学习-inception模块介绍
Inception模块

or
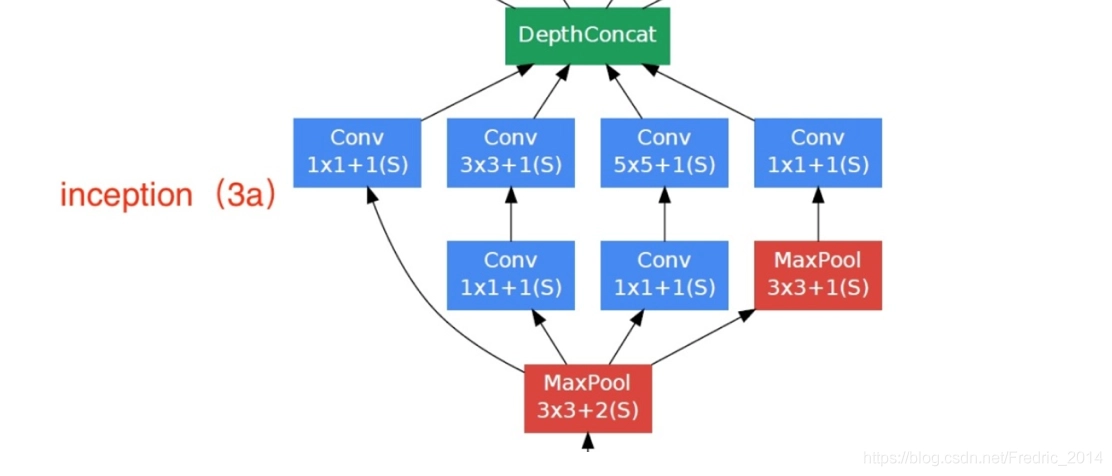
Inception模块设计了一个局部的网络拓扑结构,然后将这些模块堆叠在一起形成一个抽象层网络结构。具体来说就是运用几个并行的滤波器对输入
进行卷积和池化,这些滤波器有不同的感受野,
最后将输出的结果按深度拼接在一起形成输出层。
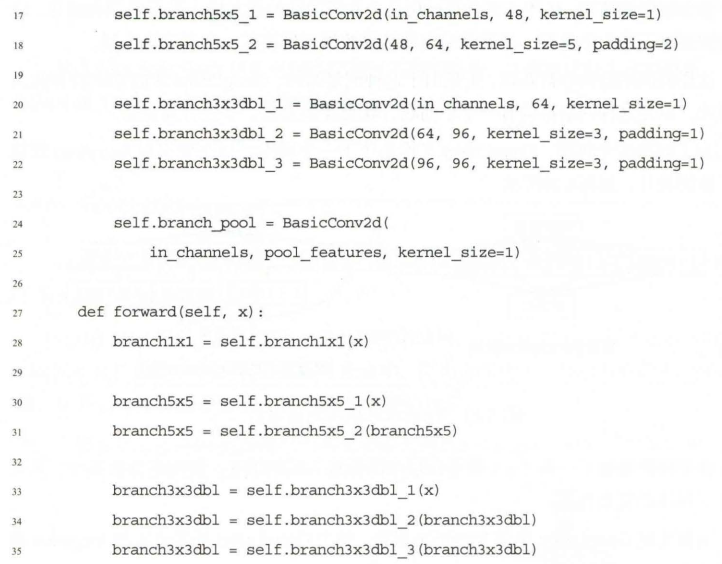
模板代码如下:



前面我们讲的 VGG 是 2014 年 ImageNet 比赛的亚军,那么冠军是谁呢?就是我们马上要讲的 GoogLeNet,这是 Google 的研究人员提出的网络结构,在当时取得了非常大的影响,因为网络的结构变得前所未有,它颠覆了大家对卷积网络的串联的印象和固定做法,采用了一种非常有效的 inception 模块,得到了比 VGG 更深的网络结构,但是却比 VGG 的参数更少,因为其去掉了后面的全连接层,所以参数大大减少,同时有了很高的计算效率。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4vYpXyFN-1672578425493)(null)]
这是 googlenet 的网络示意图,下面我们介绍一下其作为创新的 inception 模块。
Inception 模块
在上面的网络中,我们看到了多个四个并行卷积的层,这些四个卷积并行的层就是 inception 模块,可视化如下
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uVKMbdHQ-1672578425321)(null)]
一个 inception 模块的四个并行线路如下:
1.一个 1 x 1 的卷积,一个小的感受野进行卷积提取特征
2.一个 1 x 1 的卷积加上一个 3 x 3 的卷积,1 x 1 的卷积降低输入的特征通道,减少参数计算量,然后接一个 3 x 3 的卷积做一个较大感受野的卷积
3.一个 1 x 1 的卷积加上一个 5 x 5 的卷积,作用和第二个一样
4.一个 3 x 3 的最大池化加上 1 x 1 的卷积,最大池化改变输入的特征排列,1 x 1 的卷积进行特征提取
最后将四个并行线路得到的特征在通道这个维度上拼接在一起,下面我们可以实现一下
import sys
sys.path.append('..')
import numpy as np
import torch
from torch import nn
from torch.autograd import Variable
from torchvision.datasets import CIFAR10
# 定义一个卷积加一个 relu 激活函数和一个 batchnorm 作为一个基本的层结构
def conv_relu(in_channel, out_channel, kernel, stride=1, padding=0):
layer = nn.Sequential(
nn.Conv2d(in_channel, out_channel, kernel, stride, padding),
nn.BatchNorm2d(out_channel, eps=1e-3),
nn.ReLU(True)
)
return layer
class inception(nn.Module):
def __init__(self, in_channel, out1_1, out2_1, out2_3, out3_1, out3_5, out4_1):
super(inception, self).__init__()
# 第一条线路
self.branch1x1 = conv_relu(in_channel, out1_1, 1)
# 第二条线路
self.branch3x3 = nn.Sequential(
conv_relu(in_channel, out2_1, 1),
conv_relu(out2_1, out2_3, 3, padding=1)
)
# 第三条线路
self.branch5x5 = nn.Sequential(
conv_relu(in_channel, out3_1, 1),
conv_relu(out3_1, out3_5, 5, padding=2)
)
# 第四条线路
self.branch_pool = nn.Sequential(
nn.MaxPool2d(3, stride=1, padding=1),
conv_relu(in_channel, out4_1, 1)
)
def forward(self, x):
f1 = self.branch1x1(x)
f2 = self.branch3x3(x)
f3 = self.branch5x5(x)
f4 = self.branch_pool(x)
output = torch.cat((f1, f2, f3, f4), dim=1)
return output
test_net = inception(3, 64, 48, 64, 64, 96, 32)
test_x = Variable(torch.zeros(1, 3, 96, 96))
print('input shape: {} x {} x {}'.format(test_x.shape[1], test_x.shape[2], test_x.shape[3]))
test_y = test_net(test_x)
print('output shape: {} x {} x {}'.format(test_y.shape[1], test_y.shape[2], test_y.shape[3]))
input shape: 3 x 96 x 96
output shape: 256 x 96 x 96
可以看到输入经过了 inception 模块之后,大小没有变化,通道的维度变多了
下面我们定义 GoogLeNet,GoogLeNet 可以看作是很多个 inception 模块的串联,注意,原论文中使用了多个输出来解决梯度消失的问题,这里我们只定义一个简单版本的 GoogLeNet,简化为一个输出
class googlenet(nn.Module):
def __init__(self, in_channel, num_classes, verbose=False):
super(googlenet, self).__init__()
self.verbose = verbose
self.block1 = nn.Sequential(
conv_relu(in_channel, out_channel=64, kernel=7, stride=2, padding=3),
nn.MaxPool2d(3, 2)
)
self.block2 = nn.Sequential(
conv_relu(64, 64, kernel=1),
conv_relu(64, 192, kernel=3, padding=1),
nn.MaxPool2d(3, 2)
)
self.block3 = nn.Sequential(
inception(192, 64, 96, 128, 16, 32, 32),
inception(256, 128, 128, 192, 32, 96, 64),
nn.MaxPool2d(3, 2)
)
self.block4 = nn.Sequential(
inception(480, 192, 96, 208, 16, 48, 64),
inception(512, 160, 112, 224, 24, 64, 64),
inception(512, 128, 128, 256, 24, 64, 64),
inception(512, 112, 144, 288, 32, 64, 64),
inception(528, 256, 160, 320, 32, 128, 128),
nn.MaxPool2d(3, 2)
)
self.block5 = nn.Sequential(
inception(832, 256, 160, 320, 32, 128, 128),
inception(832, 384, 182, 384, 48, 128, 128),
nn.AvgPool2d(2)
)
self.classifier = nn.Linear(1024, num_classes)
def forward(self, x):
x = self.block1(x)
if self.verbose:
print('block 1 output: {}'.format(x.shape))
x = self.block2(x)
if self.verbose:
print('block 2 output: {}'.format(x.shape))
x = self.block3(x)
if self.verbose:
print('block 3 output: {}'.format(x.shape))
x = self.block4(x)
if self.verbose:
print('block 4 output: {}'.format(x.shape))
x = self.block5(x)
if self.verbose:
print('block 5 output: {}'.format(x.shape))
x = x.view(x.shape[0], -1)
x = self.classifier(x)
return x
test_net = googlenet(3, 10, True)
test_x = Variable(torch.zeros(1, 3, 96, 96))
test_y = test_net(test_x)
print('output: {}'.format(test_y.shape))
block 1 output: torch.Size([1, 64, 23, 23])
block 2 output: torch.Size([1, 192, 11, 11])
block 3 output: torch.Size([1, 480, 5, 5])
block 4 output: torch.Size([1, 832, 2, 2])
block 5 output: torch.Size([1, 1024, 1, 1])
output: torch.Size([1, 10])
可以看到输入的尺寸不断减小,通道的维度不断增加
from utils import train
def data_tf(x):
x = x.resize((96, 96), 2) # 将图片放大到 96 x 96
x = np.array(x, dtype='float32') / 255
x = (x - 0.5) / 0.5 # 标准化,这个技巧之后会讲到
x = x.transpose((2, 0, 1)) # 将 channel 放到第一维,只是 pytorch 要求的输入方式
x = torch.from_numpy(x)
return x
train_set = CIFAR10('./data', train=True, transform=data_tf)
train_data = torch.utils.data.DataLoader(train_set, batch_size=64, shuffle=True)
test_set = CIFAR10('./data', train=False, transform=data_tf)
test_data = torch.utils.data.DataLoader(test_set, batch_size=128, shuffle=False)
net = googlenet(3, 10)
optimizer = torch.optim.SGD(net.parameters(), lr=0.01)
criterion = nn.CrossEntropyLoss()
train(net, train_data, test_data, 20, optimizer, criterion)
Epoch 0. Train Loss: 1.504840, Train Acc: 0.452605, Valid Loss: 1.372426, Valid Acc: 0.514339, Time 00:01:25
Epoch 1. Train Loss: 1.046663, Train Acc: 0.630734, Valid Loss: 1.147823, Valid Acc: 0.606309, Time 00:01:02
Epoch 2. Train Loss: 0.833869, Train Acc: 0.710618, Valid Loss: 1.017181, Valid Acc: 0.644284, Time 00:00:54
Epoch 3. Train Loss: 0.688739, Train Acc: 0.760670, Valid Loss: 0.847099, Valid Acc: 0.712520, Time 00:00:58
Epoch 4. Train Loss: 0.576516, Train Acc: 0.801111, Valid Loss: 0.850494, Valid Acc: 0.706487, Time 00:01:01
Epoch 5. Train Loss: 0.483854, Train Acc: 0.832241, Valid Loss: 0.802392, Valid Acc: 0.726958, Time 00:01:08
Epoch 6. Train Loss: 0.410416, Train Acc: 0.857657, Valid Loss: 0.865246, Valid Acc: 0.721618, Time 00:01:23
Epoch 7. Train Loss: 0.346010, Train Acc: 0.881813, Valid Loss: 0.850472, Valid Acc: 0.729430, Time 00:01:28
Epoch 8. Train Loss: 0.289854, Train Acc: 0.900815, Valid Loss: 1.313582, Valid Acc: 0.650712, Time 00:01:22
Epoch 9. Train Loss: 0.239552, Train Acc: 0.918378, Valid Loss: 0.970173, Valid Acc: 0.726661, Time 00:01:30
Epoch 10. Train Loss: 0.212439, Train Acc: 0.927270, Valid Loss: 1.188284, Valid Acc: 0.665843, Time 00:01:29
Epoch 11. Train Loss: 0.175206, Train Acc: 0.939758, Valid Loss: 0.736437, Valid Acc: 0.790051, Time 00:01:29
Epoch 12. Train Loss: 0.140491, Train Acc: 0.952366, Valid Loss: 0.878171, Valid Acc: 0.764241, Time 00:01:14
Epoch 13. Train Loss: 0.127249, Train Acc: 0.956981, Valid Loss: 1.159881, Valid Acc: 0.731309, Time 00:01:00
Epoch 14. Train Loss: 0.108748, Train Acc: 0.962836, Valid Loss: 1.234320, Valid Acc: 0.716377, Time 00:01:23
Epoch 15. Train Loss: 0.091655, Train Acc: 0.969030, Valid Loss: 0.822575, Valid Acc: 0.790348, Time 00:01:28
Epoch 16. Train Loss: 0.086218, Train Acc: 0.970309, Valid Loss: 0.943607, Valid Acc: 0.767306, Time 00:01:24
Epoch 17. Train Loss: 0.069979, Train Acc: 0.976822, Valid Loss: 1.038973, Valid Acc: 0.755340, Time 00:01:22
Epoch 18. Train Loss: 0.066750, Train Acc: 0.977322, Valid Loss: 0.838827, Valid Acc: 0.801226, Time 00:01:23
Epoch 19. Train Loss: 0.052757, Train Acc: 0.982577, Valid Loss: 0.876127, Valid Acc: 0.796479, Time 00:01:25
GoogLeNet 加入了更加结构化的 Inception 块使得我们能够使用更大的通道,更多的层,同时也控制了计算量。
**小练习:GoogLeNet 有很多后续的版本,尝试看看论文,看看有什么不同,实现一下:
v1:最早的版本
v2:加入 batch normalization 加快训练
v3:对 inception 模块做了调整
v4:基于 ResNet 加入了 残差连接 **
ResNet
ResNet是2015年ImageNet竞赛的冠军,由微软研究院提出。
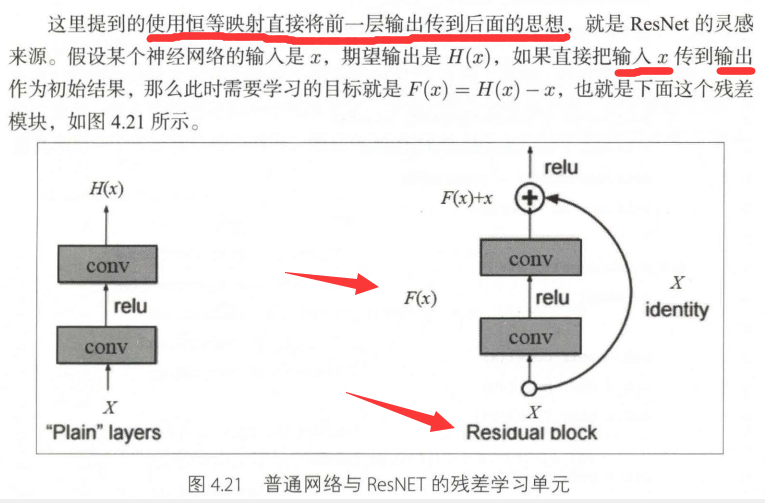




从forward 的最后一行, 能够看出网络将最开始的x加到了输出当中,形成了残差结构。
当大家还在惊叹 GoogLeNet 的 inception 结构的时候,微软亚洲研究院的研究员已经在设计更深但结构更加简单的网络 ResNet,并且凭借这个网络子在 2015 年 ImageNet 比赛上大获全胜。
ResNet 有效地解决了深度神经网络难以训练的问题,可以训练高达 1000 层的卷积网络。网络之所以难以训练,是因为存在着梯度消失的问题,离 loss 函数越远的层,在反向传播的时候,梯度越小,就越难以更新,随着层数的增加,这个现象越严重。之前有两种常见的方案来解决这个问题:
1.按层训练,先训练比较浅的层,然后在不断增加层数,但是这种方法效果不是特别好,而且比较麻烦
2.使用更宽的层,或者增加输出通道,而不加深网络的层数,这种结构往往得到的效果又不好
ResNet 通过引入了跨层链接解决了梯度回传消失的问题。
这就普通的网络连接跟跨层残差连接的对比图,使用普通的连接,上层的梯度必须要一层一层传回来,而是用残差连接,相当于中间有了一条更短的路,梯度能够从这条更短的路传回来,避免了梯度过小的情况。
假设某层的输入是 x,期望输出是 H(x), 如果我们直接把输入 x 传到输出作为初始结果,这就是一个更浅层的网络,更容易训练,而这个网络没有学会的部分,我们可以使用更深的网络 F(x) 去训练它,使得训练更加容易,最后希望拟合的结果就是 F(x) = H(x) - x,这就是一个残差的结构
残差网络的结构就是上面这种残差块的堆叠,下面让我们来实现一个 residual block
import sys
sys.path.append('..')
import numpy as np
import torch
from torch import nn
import torch.nn.functional as F
from torch.autograd import Variable
from torchvision.datasets import CIFAR10
def conv3x3(in_channel, out_channel, stride=1):
return nn.Conv2d(in_channel, out_channel, 3, stride=stride, padding=1, bias=False)
class residual_block(nn.Module):
def __init__(self, in_channel, out_channel, same_shape=True):
super(residual_block, self).__init__()
self.same_shape = same_shape
stride=1 if self.same_shape else 2
self.conv1 = conv3x3(in_channel, out_channel, stride=stride)
self.bn1 = nn.BatchNorm2d(out_channel)
self.conv2 = conv3x3(out_channel, out_channel)
self.bn2 = nn.BatchNorm2d(out_channel)
if not self.same_shape:
self.conv3 = nn.Conv2d(in_channel, out_channel, 1, stride=stride)
def forward(self, x):
out = self.conv1(x)
out = F.relu(self.bn1(out), True)
out = self.conv2(out)
out = F.relu(self.bn2(out), True)
if not self.same_shape:
x = self.conv3(x)
return F.relu(x+out, True)
我们测试一下一个 residual block 的输入和输出
# 输入输出形状相同
test_net = residual_block(32, 32)
test_x = Variable(torch.zeros(1, 32, 96, 96))
print('input: {}'.format(test_x.shape))
test_y = test_net(test_x)
print('output: {}'.format(test_y.shape))
input: torch.Size([1, 32, 96, 96])
output: torch.Size([1, 32, 96, 96])
# 输入输出形状不同
test_net = residual_block(3, 32, False)
test_x = Variable(torch.zeros(1, 3, 96, 96))
print('input: {}'.format(test_x.shape))
test_y = test_net(test_x)
print('output: {}'.format(test_y.shape))
input: torch.Size([1, 3, 96, 96])
output: torch.Size([1, 32, 48, 48])
下面我们尝试实现一个 ResNet,它就是 residual block 模块的堆叠
class resnet(nn.Module):
def __init__(self, in_channel, num_classes, verbose=False):
super(resnet, self).__init__()
self.verbose = verbose
self.block1 = nn.Conv2d(in_channel, 64, 7, 2)
self.block2 = nn.Sequential(
nn.MaxPool2d(3, 2),
residual_block(64, 64),
residual_block(64, 64)
)
self.block3 = nn.Sequential(
residual_block(64, 128, False),
residual_block(128, 128)
)
self.block4 = nn.Sequential(
residual_block(128, 256, False),
residual_block(256, 256)
)
self.block5 = nn.Sequential(
residual_block(256, 512, False),
residual_block(512, 512),
nn.AvgPool2d(3)
)
self.classifier = nn.Linear(512, num_classes)
def forward(self, x):
x = self.block1(x)
if self.verbose:
print('block 1 output: {}'.format(x.shape))
x = self.block2(x)
if self.verbose:
print('block 2 output: {}'.format(x.shape))
x = self.block3(x)
if self.verbose:
print('block 3 output: {}'.format(x.shape))
x = self.block4(x)
if self.verbose:
print('block 4 output: {}'.format(x.shape))
x = self.block5(x)
if self.verbose:
print('block 5 output: {}'.format(x.shape))
x = x.view(x.shape[0], -1)
x = self.classifier(x)
return x
输出一下每个 block 之后的大小
test_net = resnet(3, 10, True)
test_x = Variable(torch.zeros(1, 3, 96, 96))
test_y = test_net(test_x)
print('output: {}'.format(test_y.shape))
block 1 output: torch.Size([1, 64, 45, 45])
block 2 output: torch.Size([1, 64, 22, 22])
block 3 output: torch.Size([1, 128, 11, 11])
block 4 output: torch.Size([1, 256, 6, 6])
block 5 output: torch.Size([1, 512, 1, 1])
output: torch.Size([1, 10])
from utils import train
def data_tf(x):
x = x.resize((96, 96), 2) # 将图片放大到 96 x 96
x = np.array(x, dtype='float32') / 255
x = (x - 0.5) / 0.5 # 标准化,这个技巧之后会讲到
x = x.transpose((2, 0, 1)) # 将 channel 放到第一维,只是 pytorch 要求的输入方式
x = torch.from_numpy(x)
return x
train_set = CIFAR10('./data', train=True, transform=data_tf)
train_data = torch.utils.data.DataLoader(train_set, batch_size=64, shuffle=True)
test_set = CIFAR10('./data', train=False, transform=data_tf)
test_data = torch.utils.data.DataLoader(test_set, batch_size=128, shuffle=False)
net = resnet(3, 10)
optimizer = torch.optim.SGD(net.parameters(), lr=0.01)
criterion = nn.CrossEntropyLoss()
train(net, train_data, test_data, 20, optimizer, criterion)
Epoch 0. Train Loss: 1.437317, Train Acc: 0.476662, Valid Loss: 1.928288, Valid Acc: 0.384691, Time 00:00:44
Epoch 1. Train Loss: 0.992832, Train Acc: 0.648198, Valid Loss: 1.009847, Valid Acc: 0.642405, Time 00:00:48
Epoch 2. Train Loss: 0.767309, Train Acc: 0.732617, Valid Loss: 1.827319, Valid Acc: 0.430380, Time 00:00:47
Epoch 3. Train Loss: 0.606737, Train Acc: 0.788043, Valid Loss: 1.304808, Valid Acc: 0.585245, Time 00:00:46
Epoch 4. Train Loss: 0.484436, Train Acc: 0.834499, Valid Loss: 1.335749, Valid Acc: 0.617089, Time 00:00:47
Epoch 5. Train Loss: 0.374320, Train Acc: 0.872922, Valid Loss: 0.878519, Valid Acc: 0.724288, Time 00:00:47
Epoch 6. Train Loss: 0.280981, Train Acc: 0.904212, Valid Loss: 0.931616, Valid Acc: 0.716871, Time 00:00:48
Epoch 7. Train Loss: 0.210800, Train Acc: 0.929747, Valid Loss: 1.448870, Valid Acc: 0.638548, Time 00:00:48
Epoch 8. Train Loss: 0.147873, Train Acc: 0.951427, Valid Loss: 1.356992, Valid Acc: 0.657536, Time 00:00:47
Epoch 9. Train Loss: 0.112824, Train Acc: 0.963895, Valid Loss: 1.630560, Valid Acc: 0.627769, Time 00:00:47
Epoch 10. Train Loss: 0.082685, Train Acc: 0.973905, Valid Loss: 0.982882, Valid Acc: 0.744264, Time 00:00:44
Epoch 11. Train Loss: 0.065325, Train Acc: 0.979680, Valid Loss: 0.911631, Valid Acc: 0.767009, Time 00:00:47
Epoch 12. Train Loss: 0.041401, Train Acc: 0.987952, Valid Loss: 1.167992, Valid Acc: 0.729826, Time 00:00:48
Epoch 13. Train Loss: 0.037516, Train Acc: 0.989011, Valid Loss: 1.081807, Valid Acc: 0.746737, Time 00:00:47
Epoch 14. Train Loss: 0.030674, Train Acc: 0.991468, Valid Loss: 0.935292, Valid Acc: 0.774031, Time 00:00:45
Epoch 15. Train Loss: 0.021743, Train Acc: 0.994565, Valid Loss: 0.879348, Valid Acc: 0.790150, Time 00:00:47
Epoch 16. Train Loss: 0.014642, Train Acc: 0.996463, Valid Loss: 1.328587, Valid Acc: 0.724387, Time 00:00:47
Epoch 17. Train Loss: 0.011072, Train Acc: 0.997363, Valid Loss: 0.909065, Valid Acc: 0.792919, Time 00:00:47
Epoch 18. Train Loss: 0.006870, Train Acc: 0.998561, Valid Loss: 0.923746, Valid Acc: 0.794403, Time 00:00:46
Epoch 19. Train Loss: 0.004240, Train Acc: 0.999500, Valid Loss: 0.877908, Valid Acc: 0.802314, Time 00:00:46
ResNet 使用跨层通道使得训练非常深的卷积神经网络成为可能。同样它使用很简单的卷积层配置,使得其拓展更加简单。
小练习:
1.尝试一下论文中提出的 bottleneck 的结构
2.尝试改变 conv -> bn -> relu 的顺序为 bn -> relu -> conv,看看精度会不会提高
案例-MNIST手写数字分类




实现cifar10分类
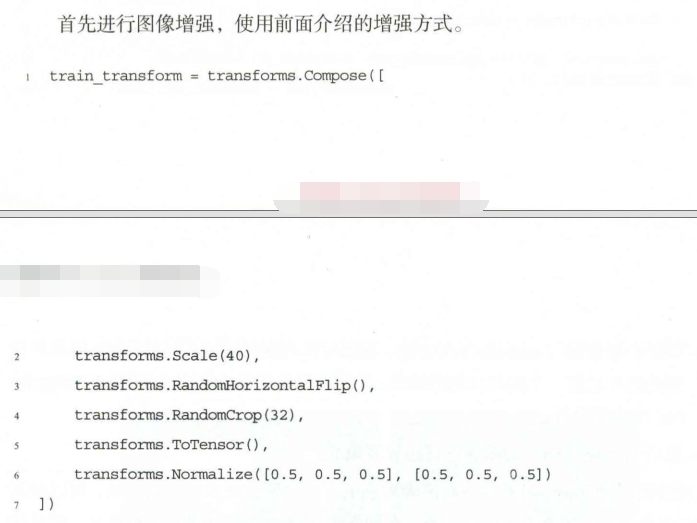
图像增强

定义基本模块