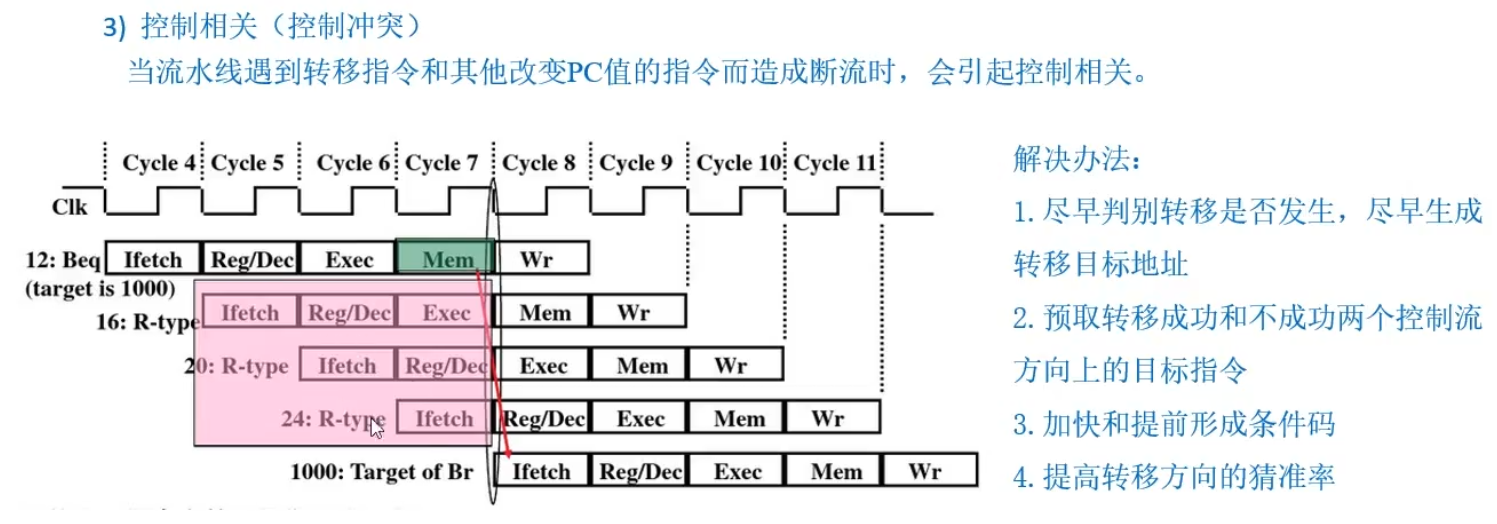
查找算法【二叉查找树】 - 二叉查找树的插入

因为二叉查找树的中序遍历存在有序性，所以首先要查找待插入关键字的插入位置，当查找不成功时，再将待插入关键字作为新的叶子节点成为最后一个查找节点的左孩子或右孩子。

【算法步骤】

① 若二叉查找树为空，则创建一个新的节点s ，将待插入关键字放入新节点的数据域，将s 节点作为根节点，左右子树均为空。

② 若二叉查找树非空，则将待查找关键字x 与根节点的关键字T->data进行比较。

• 若x <T ->data，则将x 插入左子树中。
• 若x >T ->data，则将x 插入右子树中。

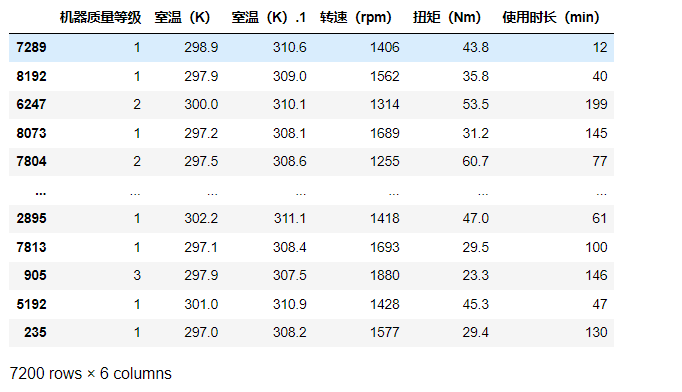
【举个栗子】

一棵二叉查找树如下图所示，向其中插入关键字30。

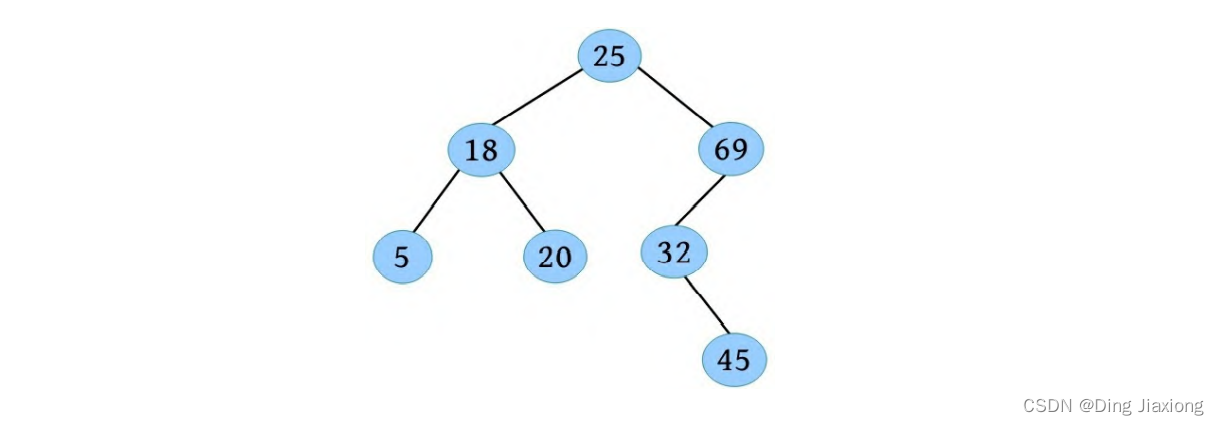
① 将30与树根25进行比较，30>25，在25的右子树中查找，如下图所示。

② 将30与右子树的树根69进行比较，30<69，在69的左子树中查找，如下图所示。

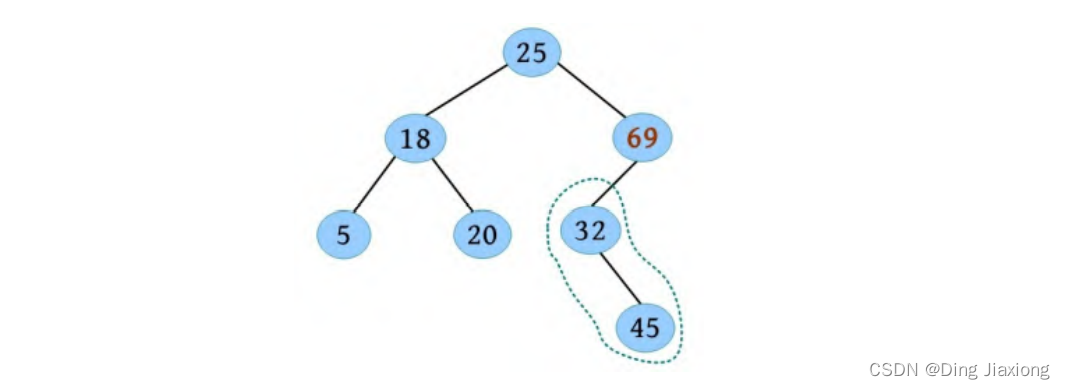
③ 将30与左子树的树根32进行比较，30<32，在32的左子树中查找，如下图所示。

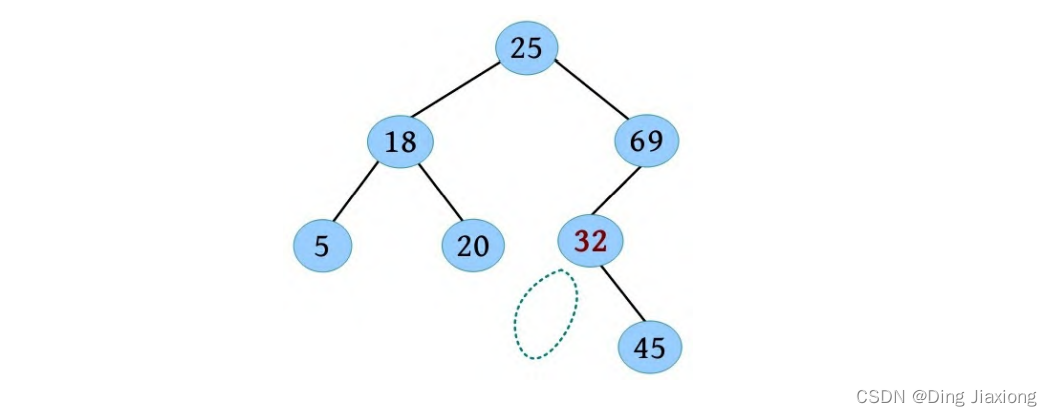
④ 32的左子树为空，将30作为新的叶子节点插入32的左子树中，如下图所示。

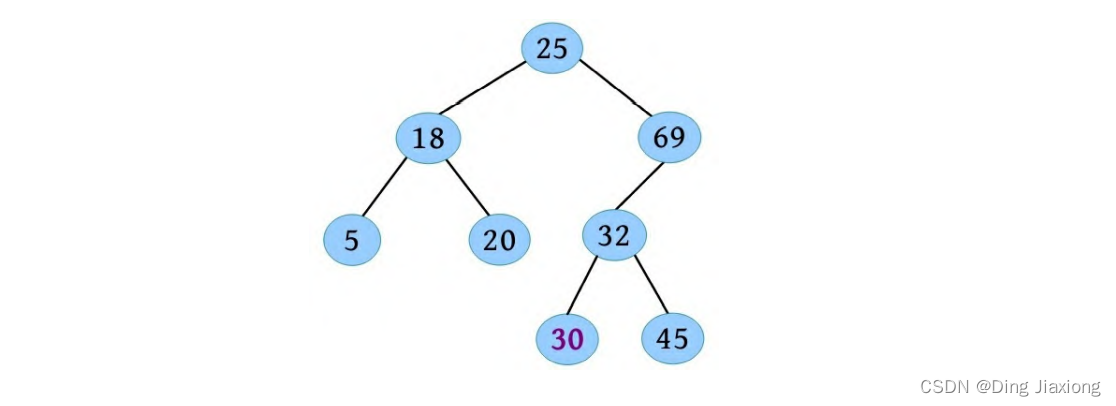
【算法实现】

void InsertBST(BSTree &T , ElemType e){ //二叉查找树的插入
	//当二叉排序树T 中不存在关键字等于e 的数据元素时，插入该元素
	if(!T){
		BSTree S = new BSTNode;  //生成新节点
		S-> data = e; //将新节点S的数据域置为e
		S-> lchild = S -> rchild = NULL; //将新节点S作为叶子节点
		T = S; //将新节点S 链接到已找到的插入位置
	}
	else if(e < T-> data){
		InsertBST(T->lchild , e); //插入左子树
	}
	else if(e > T->data){
		InsertBST(T->rchild , e); //插入右子树
	}
}

【算法分析】

在二叉查找树中进行插入操作时需要先查找插入位置，插入本身只需要常数时间，但查找插入位置的时间复杂度为O (logn )。