一、NVM：Node Version Management；

下载地址：Releases · coreybutler/nvm-windows · GitHubA node.js version management utility for Windows. Ironically written in Go. - Releases · coreybutler/nvm-windowshttps://github.com/coreybutler/nvm-windows/releasesnode的版本管理工具，轻松实现不同版本node的安装与切换。

二、常用命令；

1、查看node版本；

# 查看当前使用node版本；

node  -v

 

# 查看本地已安装的`Node`版本列表（`list`可简化为`ls`）
nvm list

或  nvm ls

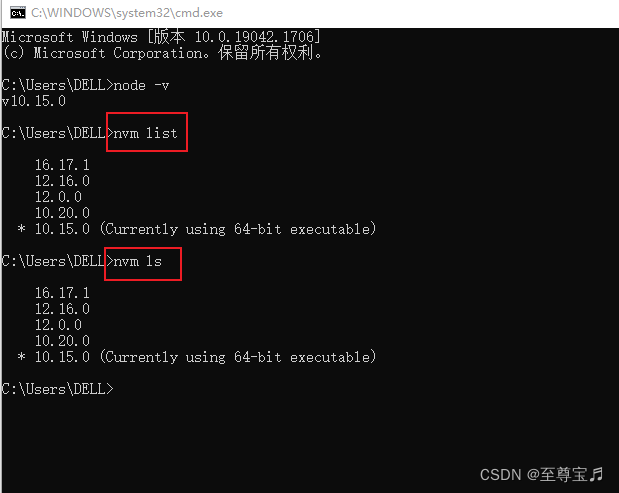
2、安装指定版本的node;

# 安装指定版本的`Node`（`version`是版本号）。
nvm install <'version'>

# 安装最新版本，用`latest`
nvm install latest

 

 # 安装最新稳定版本；

nvm install stable 

（测试后，好像没啥效果）

#  `arch`指定安装`32`位还是`64`位版本（可选参数，默认是系统位数）。
# 可以添加`--insecure`绕过远程服务器的`SSL`。
nvm install <'version'> ['arch'] ['--insecure']

3、node版本切换；

# 切换指定`Node`版本（可指定`32`/`64`位）。
nvm use  <'version'>  ['arch']

# 比如切换`16.17.1`版本。
nvm use 16.17.1

报错如下；

 原因：当前打开命令提示框的权限是user，无法切换node版本。

解决方法：用管理员身份打开命令框，执行命令即可，如下图所示；

 

 4、卸载指定版本的node;（命令提示框用user权限即可）

# 卸载`Node`版本
nvm uninstall <'version'>

# 比如：卸载`12.0.0`版本
nvm uninstall 12.0.0

  三、应用案例：

 

 

 

四、备注：

node安装包下载地址：

Download | Node.js

 Previous Releases | Node.js