DeepGCNs: Can GCNs Go as Deep as CNNs?
- 绪论
- 1、介绍
- 2、相关工作
- 3、方法
- 3.1、图神经网络的表针学习
- 3.2、图神经网络的残差结构
- 3.3、图神经网络的密集连接
- 3.4、图神经网络的扩张性聚集
绪论
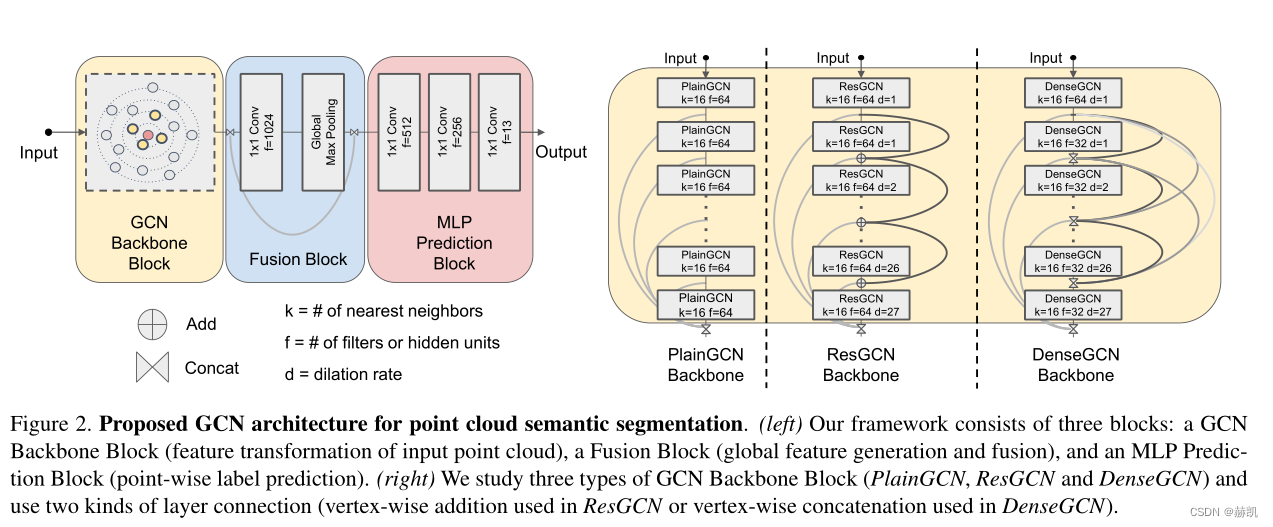
CNN很强,但不能正确解决非欧几里得数据的问题,图卷积网络(GCNs)可以建立图形来表示非欧几里得数据,借鉴CNN的概念,并将其应用到训练中。GCN有点作用但有梯度消失的问题,限制在很浅的模型。这篇论文就可以成功训练出非常深的GCN。通过借用CNN的概念,特别是残差/密集连接和扩张卷积,并将其适应于GCN架构,大量的实验显示了这些深度GCN框架的积极作用。最后,使用这些新概念建立了一个非常深的56层的GCN,并展示了它是如何在点云语义分割的任务中显著提高性能的(比最先进的+3.7% mIoU)。
1、介绍
在过去的几年里,GCNs获得了很大的发展势头。这种兴趣的增加主要归因于两个因素:现实世界应用中的非欧几里得数据越来越多,以及CNN在处理这些数据时性能有限。GCNs直接在非欧几里得数据上操作,对于依赖这种信息模式的应用是非常有前途的。目前,GCNs被用来预测社交网络中的个体关系,为药物发现建立蛋白质模型,加强推荐引擎的预测,有效分割大型点云,以及其他领域。
CNN成功背后的一个关键原因是能够设计并可靠地训练非常深的CNN模型。相比之下,目前还不清楚如何正确地训练深度GCN架构,有几项工作已经研究了它们的局限性。将更多的层堆叠到GCN中会导致常见的梯度消失问题。这意味着通过这些网络的反向传播会导致过度平滑,最终导致图形顶点的特征收敛到同一数值。由于这些限制,大多数最先进的GCN的深度不超过4层。
对于梯度消失,CNN引入了RESNet,GCN看下能不能模仿下。在这篇文章借鉴了CNN的一些网络结构,也可以构建深层次的网络模型。
贡献:将残差/密集连接和扩张卷积适应于GCNs。在点云数据上进行了广泛的实验,展示了这些新层对训练深度GCN的稳定性和性能的影响。我们使用点云的语义分割作为我们的实验测试平台。展示了这些新概念如何帮助建立一个56层的GCN,这是最深的GCN架构,并在S3DIS数据集上实现接近4%的性能提升。
2、相关工作
因为在现实世界中,非欧几里得结构的数据比较多,而CNN没有办法处理,所以图神经网络就出来了。
它是一类不具有平移不变性的数据。这类数据以其中的一个为节点,其邻居节点的数量可能不同。常见这类数据有知识图谱、社交网络、化学分子结构等等。
图神经网络借鉴CNN残差/密集连接和扩张卷积,来加深网络。
3、方法
3.1、图神经网络的表针学习
图的定义。图 G G G由一个元组 G = ( V , E ) G = (V, E) G=(V,E)表示,其中 V V V是无序顶点的集合, E E E是代表顶点 v ∈ V v∈V v∈V之间连通性的边的集合,如果 e i , j ∈ E e_{i,j}∈E ei,j∈E,那么顶点 v i v_i vi和 v j v_j vj之间有一条边 e i , j e_{i,j} ei,j相连。
图卷积网络。受CNN的启发,GCN打算通过聚合其附近顶点的特征,在一个顶点上提取更丰富的特征。GCN通过将每个顶点与一个特征向量 h v ∈ R D h_v∈R^D hv∈RD相关联来表示顶点,其中 D D D是特征维度。因此,图 G G G作为一个整体可以通过串联所有无序顶点的特征来表示,即
h G = [ h v 1 , h v 2 , . . . , h v N ] > ∈ R N × D h_G = [h_{v1}, h_{v2}, ..., h_{vN} ]> ∈R^{N×D} hG=[hv1,hv2,...,hvN]>∈RN×D,其中 N N N为集合 V V V的可选域。在第 l l l层的一般图卷积操作 F F F可以被表述为以下聚合和更新操作。
G l + 1 = F ( G l , W l ) = U p d a t e ( A g g r e g a t e ( G l , W l a g g ) , W l u p d a t e ) . G_{l+1} = F(G_l, W_l) = U pdate(Aggregate(G_l, W^{agg}_l ), W^{update}_l ). Gl+1=F(Gl,Wl)=Update(Aggregate(Gl,Wlagg),Wlupdate).
G
l
=
(
V
l
,
E
l
)
G_l = (V_l, E_l)
Gl=(Vl,El) 和
G
l
+
1
=
(
V
l
+
1
,
E
l
+
1
)
G_{l+1} = (V_{l+1}, E_{l+1})
Gl+1=(Vl+1,El+1) 分别是第l层的输入和输出图。
W
l
a
g
g
W^{agg}_l
Wlagg和
W
l
u
p
d
a
t
e
W^{update}_l
Wlupdate分别是聚合函数和更新函数的可学习权重,它们是GCN的基本组成部分。在大多数GCN框架中,聚合函数用于编译顶点附近的信息,而更新函数对聚合的信息进行非线性变换以计算新的顶点表示。这两个函数有不同的变体。例如,聚合函数可以是平均聚合器、最大集合聚合器、注意聚合器或LSTM聚合器。更新函数可以是一个多层感知器,一个门控网络,等等。更具体地说,顶点的表示是在每一层通过聚合所有
v
l
+
1
∈
V
l
+
1
v_{l+1}∈V_{l+1}
vl+1∈Vl+1的邻居顶点的特征来计算的,如下所示。
h
v
l
+
1
=
ϕ
(
h
v
l
,
ρ
(
h
u
l
∣
u
l
∈
N
(
v
l
)
,
h
v
l
,
W
ρ
)
,
W
ϕ
)
,
h_{v_{l+1}} = ϕ (h_{v_l}, ρ({h_{u_l}|u_l ∈ N (v_l)}, h_{v_l}, W_ρ), W_ϕ),
hvl+1=ϕ(hvl,ρ(hul∣ul∈N(vl),hvl,Wρ),Wϕ),
其中, ρ ρ ρ为顶点特征聚合函数, ϕ ϕ ϕ为顶点特征更新函数, h v l h_{v_l} hvl和 h v l + 1 h_{v_{l+1}} hvl+1分别为第l层和第l+1层的顶点特征。 N ( v l ) N(v_l) N(vl)是 v v v在第l层的邻居顶点集合, h u l h_{u_l} hul是由 W ρ W_ρ Wρ参数化的这些邻居顶点的特征。 W ϕ W_ϕ Wϕ包含这些函数的可学习参数。为简单起见,在不丧失一般性的情况下,我们使用一个最大集合顶点特征聚合器,没有可学习的参数,以集合顶点 v l v_l vl和其所有邻居之间的特征差异。 ρ ( . ) = m a x ( h u l − h v l ∣ u l ∈ N ( v l ) ) ρ(.) = max(h_{u_l} − h{v_l}| u_l ∈ N (v_l)) ρ(.)=max(hul−hvl∣ul∈N(vl)). 然后,我们将顶点特征更新器 ϕ ϕ ϕ建模为一个多层感知器(MLP),采用批量归一化和ReLU作为激活函数。这个MLP将 h v l h_{v_l} hvl与来自 ρ ( . ) ρ(.) ρ(.)的聚合特征连接起来,形成其输入。
动态边框。如前所述,大多数GCN有固定的图形结构,并且只在每次迭代时更新顶点特征。最近的工作表明,与具有固定图形结构的GCN相比,动态图形卷积,即允许图形结构在每一层发生变化,可以学习更好的图形表示。例如,ECC(Edge-Conditioned Convolution)使用动态边缘条件过滤器来学习特定边缘的权重矩阵。此外,EdgeConv在每个EdgeConv层之后,在当前特征空间中找到最近的邻居来重建图。为了学习生成点云,Graph-Convolution GAN(生成对抗网络)也应用k-NN图来构建每层中每个顶点的邻域。我们发现,动态改变GCN中的邻域有助于缓解过度平滑问题,并且在考虑更深的GCN时,会产生一个有效的更大的感受野。在我们的框架中,我们建议在每一层的特征空间中通过Dilated k-NN函数重新计算顶点之间的边缘,以进一步增加感受野。在下文中,我们将详细描述三种可以使更深的GCN得到训练的操作:剩余连接、密集连接和扩张聚合。
3.2、图神经网络的残差结构
3.3、图神经网络的密集连接
3.4、图神经网络的扩张性聚集







](https://img-blog.csdnimg.cn/img_convert/e6676e08e1a2e253e9f6e3de05cd34c8.png)