文章目录
- 基本简介
- 调试准备
- 损失函数
基本简介
损失函数是神经网络的重要组成部分,用于评估网络的预测值和真实值的差异度。根据偏差的大小,反向调整网络的训练参数,迭代优化使得损失尽量小,也就得到最优的网络参数。
调试准备
-
debug 设置
具体设置可以参考上一篇博文: YOLO-V5 系列算法和代码解析(三)—— 训练数据加载。调试过程中,为了避免输出的中间变量太长,关闭【mosaic】数据增强功能。关闭方法:【data/hyps/hyp.scratch-low.yaml,L32】,调整如下# mosaic: 1.0 # image mosaic (probability) mosaic:0.0 -
数据准备
调试损失函数所用图片为【000000000623.jpg】

上面图片对应的标签如下:
# --- 上面图片对应的标签 # classID,x,y,w,h(归一化) 13 0.86172 0.38362 0.27656 0.47676 77 0.4764 0.52584 0.946827 0.92584 56 0.86248 0.36568 0.265653 0.47968 0 0.71516 0.49351 0.564507 0.98182
损失函数
YOLO-V5 中的损失函数计算类主要包括:
- 类初始好化:设置参数,以及不同的损失函数API;
- 扩增正样本:生成更多的正样本;
- 计算损失 :类别损失,定位损失,置信度损失;
-
损失函数的代码结构
主要从【整体上】领略损失函数的代码结构,明确每一部分的功能,特省略详细的实现代码。整体结构如下,class ComputeLoss: sort_obj_iou = False # Compute losses def __init__(self, model, autobalance=False): device = next(model.parameters()).device # get model device h = model.hyp # hyperparameters # Define criteria # 定义类别损失和置信度损失 BCEcls = nn.BCEWithLogitsLoss(pos_weight=torch.tensor([h['cls_pw']], device=device)) BCEobj = nn.BCEWithLogitsLoss(pos_weight=torch.tensor([h['obj_pw']], device=device)) # Class label smoothing https://arxiv.org/pdf/1902.04103.pdf eqn 3 self.cp, self.cn = smooth_BCE(eps=h.get('label_smoothing', 0.0)) # positive, negative BCE targets # Focal loss # 目标检测中,用于降低类别不平衡造成的影响 g = h['fl_gamma'] # focal loss gamma if g > 0: BCEcls, BCEobj = FocalLoss(BCEcls, g), FocalLoss(BCEobj, g) m = de_parallel(model).model[-1] # Detect() module self.balance = {3: [4.0, 1.0, 0.4]}.get(m.nl, [4.0, 1.0, 0.25, 0.06, 0.02]) # P3-P7 self.ssi = list(m.stride).index(16) self.BCEcls, self.BCEobj, self.gr, self.hyp, self.autobalance = BCEcls, BCEobj, 1.0, h, autobalance self.na = m.na # number of anchors self.nc = m.nc # number of classes self.nl = m.nl # number of layers self.anchors = m.anchors self.device = device # 损失函数计算的核心函数,计算三种损失 def __call__(self, p, targets): # predictions, targets lcls = torch.zeros(1, device=self.device) # class loss lbox = torch.zeros(1, device=self.device) # box loss lobj = torch.zeros(1, device=self.device) # object loss tcls, tbox, indices, anchors = self.build_targets(p, targets) # targets """ 此处省略代码,后续会继续解析该部分代码 """ # 扩增正样本的核心函数 def build_targets(self, p, targets): """ 此处省略代码,后续会继续解析该部分代码 """ -
扩增正样本
在目标检测中,通常背景(负样本)占据比例较大,为了降低正负样本的失衡程度,需要扩增正样本。在YOLO-V5的代码中,是在正样本的上,下,左,右四个位置进行扩增。 代码位置:~/yolov5/utils/loss.py,L177.
在讲解扩增正样本代码之前,需要先直观上理解YOLO-V5中扩增正样本的核心思想。那么具体阅读代码时,也就更容易理解作者代码上的实现逻辑。大致的步骤如下,(1) 输入数据准备:扩增正样本是基于网络输出层,Anchor,真实标注框等输入信息进行处理,也是
build_targets()函数的已知条件,代码片段如下,仔细阅读代码中的注释内容,def build_targets(self, p, targets): # Build targets for compute_loss(), input targets(image,class,x,y,w,h) na, nt = self.na, targets.shape[0] # number of anchors, targets tcls, tbox, indices, anch = [], [], [], [] gain = torch.ones(7, device=self.device) # normalized to gridspace gain ai = torch.arange(na, device=self.device).float().view(na, 1).repeat(1, nt) # same as .repeat_interleave(nt) targets = torch.cat((targets.repeat(na, 1, 1), ai[..., None]), 2) # append anchor indices # ai: 用于给anchor赋予ID # ai.shape: [3,4], 每个尺度下有三个anchor, 索引为(0,1,2), 4表示输入图片中总共有4个标注框 # tensor([[0., 0., 0., 0.], # [1., 1., 1., 1.], # [2., 2., 2., 2.]], device='cuda:0') # targets: 真实标签,被复制三份([4,6]->[3,4,6]),便于和anchor进行运算, # 与ai合并后,targets变为[3,4,7], 最后一个维度是anchors的索引,标记anchor和真实框的对应关系 # tensor([[[ 0.00000, 13.00000, 0.73501, 0.37763, 0.20976, 0.48214, 0.00000], # [ 0.00000, 77.00000, 0.44276, 0.52145, 0.71813, 0.93628, 0.00000], # [ 0.00000, 56.00000, 0.73559, 0.35948, 0.20149, 0.48509, 0.00000], # [ 0.00000, 0.00000, 0.62385, 0.49260, 0.42815, 0.98520, 0.00000]], # [[ 0.00000, 13.00000, 0.73501, 0.37763, 0.20976, 0.48214, 1.00000], # [ 0.00000, 77.00000, 0.44276, 0.52145, 0.71813, 0.93628, 1.00000], # [ 0.00000, 56.00000, 0.73559, 0.35948, 0.20149, 0.48509, 1.00000], # [ 0.00000, 0.00000, 0.62385, 0.49260, 0.42815, 0.98520, 1.00000]], # [[ 0.00000, 13.00000, 0.73501, 0.37763, 0.20976, 0.48214, 2.00000], # [ 0.00000, 77.00000, 0.44276, 0.52145, 0.71813, 0.93628, 2.00000], # [ 0.00000, 56.00000, 0.73559, 0.35948, 0.20149, 0.48509, 2.00000], # [ 0.00000, 0.00000, 0.62385, 0.49260, 0.42815, 0.98520, 2.00000]]], # device='cuda:0')(2) 根据 Anchor 和标注框的宽高比例筛选标注框: 网络输出三层的【shape】分别为【1,3,80,80,85】,【1,3,40,40,85】,【1,3,20,20,85】,这些输出应该与哪些标注框进行损失计算?三组不同尺度的【Anchor】依次从真实框中筛选出符合一定尺度比例的框{Box}集合,这是第一次进行框的筛选,这一步骤为了解决【真实标注框】应该归属那一层输出的问题。具体的公式表达如下图所示,

三组不同尺度的【Anchor】如下图所示,数值已经转换到特征图尺度下的大小,
下面的代码片段则是具体的实现代码,至此则完成每一组尺度下【Anchor】与真实框的匹配过程,# Matches r = t[..., 4:6] / anchors[:, None] # wh ratio j = torch.max(r, 1 / r).max(2)[0] < self.hyp['anchor_t'] # compare # j = wh_iou(anchors, t[:, 4:6]) > model.hyp['iou_t'] # iou(3,n)=wh_iou(anchors(3,2), # gwh(n,2)) t = t[j] # filter,筛选符合条件的边框 # j: 表明第三个anchor匹配到2个真实框, # j: tensor([[False, False, False, False], # [False, False, False, False], # [ True, False, True, False]], device='cuda:0') # t[j]: 过滤没有匹配上的真实框,剩下的真实框如下,最后一列的ID(2)表示与第2个anchor匹配成功2个标签框 # 后续计算损失的时候,需要该ID取数据 # tensor([[ 0.00000, 13.00000, 29.40045, 15.10509, 8.39034, 19.28541, 2.00000], # [ 0.00000, 56.00000, 29.42351, 14.37940, 8.05945, 19.40353, 2.00000]])(3)扩增样本总体概述:(2)解决了归属的问题,当前步骤是增加每个标注框的数量。 基于第一次筛选的{Box}集合,可以进行正样本扩增。在具体讲解正样本扩增代码之前,先直观上理解其基本的思想。扩增的方法,简单说就是每一个边框的中心点坐标更靠近【上、下、左、右】的哪一个Grid,比如下图中的蓝色点,假设坐标为【2.1,4.4】,显然更靠近左、上Grid,那么左、上红绿Grid就为扩增正样本所在Grid;如此,该正样本(黄色)则扩充了两个正样本(红色,绿色),增加了正样本的数量,具体参考下图,

(4) 接下来,从代码的层面,逐步分析正样本扩增的过程
首先,确认正样本的可扩增方向。gxy是正样本本身的中心点坐标,用于指示【左、上】方向是否可偏移,gxi + gxy = 40(输出特征图尺寸),所以【gxy,gxi】的小数部分的和为1,那么必然是指示【右,下】方向是否可偏移。# Offsets gxy = t[:, 2:4] # grid xy gxi = gain[[2, 3]] - gxy # inverse j, k = ((gxy % 1 < g) & (gxy > 1)).T l, m = ((gxi % 1 < g) & (gxi > 1)).T j = torch.stack((torch.ones_like(j), j, k, l, m)) t = t.repeat((5, 1, 1))[j] offsets = (torch.zeros_like(gxy)[None] + off[:, None])[j]参考下面的注释,通过L2-L5行的代码,得到了【左、上、右、下】四个方向是否可偏移。L6行代码则是将正样本本身的grid和其它四个方向的grid组合起来,便于统一运算。注意【j】的形状,行数表示5个grid,列数表示边框数量的一个方向(x或者y方向)。
# (gxy % 1):取浮点数的小数部分,gxy>1(判断是否位于边界,边界不需要扩增) # tensor([[0.40045, 0.10509], # [0.42351, 0.37940]], device='cuda:0') # gxy % 1 < g(0.5): 负责该真实框Grid的左上的Grid是否为扩增正样本 # tensor([[True, True], # [True, True]], device='cuda:0') # 上面的值表明:两个框的中心均靠近左、上的Grid # gxi % 1:取浮点数的小数部分,负责该真实框Grid的右下的Grid是否为扩增正样本 # tensor([[0.59955, 0.89491], # [0.57649, 0.62060]], device='cuda:0') # gxi % 1 < g(0.5) # tensor([[False, False], # [False, False]], device='cuda:0') # j,k:负责指示当前Grid的左上的Grid,l,m:负责指示当前Grid的右下Grid # j:tensor([True, True], device='cuda:0') # 指示(2个)真实框的X方向都为true,即左侧可扩增 # k:tensor([True, True], device='cuda:0') # 指示(2个)真实框的Y方向,即上侧可扩增 # l:tensor([False, False], device='cuda:0') # 指示(2个)真实框的X方向,即右侧不可扩增 # m:tensor([False, False], device='cuda:0') # 指示(2个)真实框的Y方向,即下侧不可扩增 # j = torch.stack((torch.ones_like(j), j, k, l, m)): 【5,2】分别指示当前Grid,以及Grid的左上,右下 # 是否需要增加样本 # tensor([[ True, True], # 2个真实框本身 # [ True, True], # 2个真实框的左grid为扩增样本 # [ True, True], # 2个真实框的上grid为扩增样本 # [False, False], # 2个真实框的右grid不是扩增样本 # [False, False]], device='cuda:0') # 2个真实框的下grid不是扩增样本根据合成的扩增指示数组【j】,L7行的代码用于获取正样本本身和扩增样本。如下注释内容:先将正样本复制相同的5份(5:依次是中,左,上,右,下四个grid);然后,根据【j】索引数据,获取有效的样本。
# t.repeat((5, 1, 1)):将筛选后的正样本复制5份,便于与j(正样本扩增指示器)进行运算,留下所有的正样本 # tensor([[[ 0.00000, 13.00000, 29.40045, 15.10509, 8.39034, 19.28541, 2.00000], # [ 0.00000, 56.00000, 29.42351, 14.37940, 8.05945, 19.40353, 2.00000]], # [[ 0.00000, 13.00000, 29.40045, 15.10509, 8.39034, 19.28541, 2.00000], # [ 0.00000, 56.00000, 29.42351, 14.37940, 8.05945, 19.40353, 2.00000]], # [[ 0.00000, 13.00000, 29.40045, 15.10509, 8.39034, 19.28541, 2.00000], # [ 0.00000, 56.00000, 29.42351, 14.37940, 8.05945, 19.40353, 2.00000]], # [[ 0.00000, 13.00000, 29.40045, 15.10509, 8.39034, 19.28541, 2.00000], # [ 0.00000, 56.00000, 29.42351, 14.37940, 8.05945, 19.40353, 2.00000]], # [[ 0.00000, 13.00000, 29.40045, 15.10509, 8.39034, 19.28541, 2.00000], # [ 0.00000, 56.00000, 29.42351, 14.37940, 8.05945, 19.40353, 2.00000]]], # device='cuda:0') # t.repeat((5, 1, 1))[j]:根据指示器j,取出样本本身和扩增样本 # tensor([[ 0.00000, 13.00000, 29.40045, 15.10509, 8.39034, 19.28541, 2.00000], # [ 0.00000, 56.00000, 29.42351, 14.37940, 8.05945, 19.40353, 2.00000], # [ 0.00000, 13.00000, 29.40045, 15.10509, 8.39034, 19.28541, 2.00000], # [ 0.00000, 56.00000, 29.42351, 14.37940, 8.05945, 19.40353, 2.00000], # [ 0.00000, 13.00000, 29.40045, 15.10509, 8.39034, 19.28541, 2.00000], # [ 0.00000, 56.00000, 29.42351, 14.37940, 8.05945, 19.40353, 2.00000]], # device='cuda:0')其次,获取正样本的偏移量。
torch.zeros_like(gxy)全为0,表示正样本本身保留一份,不进行偏移。其它的方向偏移量需要按照样本数量复制相应的份数。off:【5,2】,样本个数:2,所以,(torch.zeros_like(gxy)[None] + off[:, None])的形状为【5,2,2】。这里 off 的数值为0.5或者-0.5,是为了保证样本即使偏移后,也是靠近正样本本身。offsets = (torch.zeros_like(gxy)[None] + off[:, None])[j]# (torch.zeros_like(gxy)[None] + off[:, None]): torch.Size([5, 2, 2]),按照off的shape复制5份,也是为 # 了便于和样本指示器【j】运算,中间的2是正样本的数量,最后的2表示x,y # tensor([[[ 0.00000, 0.00000], # [ 0.00000, 0.00000]], # [[ 0.50000, 0.00000], # [ 0.50000, 0.00000]], # [[ 0.00000, 0.50000], # [ 0.00000, 0.50000]], # [[-0.50000, 0.00000], # [-0.50000, 0.00000]], # [[ 0.00000, -0.50000], # [ 0.00000, -0.50000]]], device='cuda:0') # offsets:经过样本指示器筛选后,留下需要偏移的正样本 # tensor([[0.00000, 0.00000], # 正样本本身1,无偏移 # [0.00000, 0.00000], # 正样本本身2,无偏移 # [0.50000, 0.00000], # 左扩增样本1-1 # [0.50000, 0.00000], # 左扩增样本2-1 # [0.00000, 0.50000], # 上扩增样本1-1 # [0.00000, 0.50000]], device='cuda:0') # 上扩增样本1-2然后,得到正样本的索引值。如下面的代码所示,L2-L3分解所有筛选剩下的正样本,得到图像和anchor的索引值。L4-L5得到左上角grid的整数索引值。
# Define bc, gxy, gwh, a = t.chunk(4, 1) # (image, class), grid xy, grid wh, anchors a, (b, c) = a.long().view(-1), bc.long().T # anchors, image, class gij = (gxy - offsets).long() gi, gj = gij.T # grid indices # gxy: # tensor([[29.40045, 15.10509], # [29.42351, 14.37940], # [29.40045, 15.10509], # [29.42351, 14.37940], # [29.40045, 15.10509], # [29.42351, 14.37940]], device='cuda:0') # gij: 偏移后的 grid indice # tensor([[29, 15], # [29, 14], # [28, 15], # [28, 14], # [29, 14], # [29, 13]], device='cuda:0')最后,要保存特定的变量值,用于后续损失函数的计算。indices保存的是索引值,用于从网络的输出层取有效的数据,计算损失值。tbox保存边框的值(x,y,w,h),anch保存具体的anchor数值,tcls具体的类别值
# Append indices.append((b, a, gj.clamp_(0, shape[2] - 1), gi.clamp_(0, shape[3] - 1))) # image, anchor, grid tbox.append(torch.cat((gxy - gij, gwh), 1)) # box anch.append(anchors[a]) # anchors tcls.append(c) # class return tcls, tbox, indices, anch# b,a,gj,gi:根据4个记录的值,可以索引到具体grid的数据,用于后面计算损失 # b:输入图像的索引 # tensor([0, 0, 0, 0, 0, 0], device='cuda:0') # a:anchor的索引 # tensor([2, 2, 2, 2, 2, 2], device='cuda:0') # gj.clamp_(0, shape[2] - 1) # tensor([15, 14, 15, 14, 14, 13], device='cuda:0') # gi.clamp_(0, shape[3] - 1) # tensor([29, 29, 28, 28, 29, 29], device='cuda:0') # gxy - gij:框和扩增框的中心坐标,相对grid左上角的偏移量 # shape: [6,2], 每一个真实框对应三个正样本,总共6个正样本 # tensor([[0.40045, 0.10509], # 正样本1 # [0.42351, 0.37940], # 正样本2 # [1.40045, 0.10509], # 扩增正样本1-1 # [1.42351, 0.37940], # 扩增正样本2-1 # [0.40045, 1.10509], # 扩增正样本1-2 # [0.42351, 1.37940]], device='cuda:0') # 扩增正样本2-2(5) 新样本的表达方式。真实标注框的表达为(x,y,w,h),其中x,y相对于本身Grid的左上角的偏移量,那么新的扩增框的标签应该如何表达?我们应该知道,新的框也是用来表示正样本本身,那么偏移量【x,y】应是相对于正样本本身。以(3)中的扩增正样本为例,新的正样本(1.1,0.4,w,h),(0.1,1.4,w,h),本身正样本(0.1,0.4,w,h);
如此便得到了与正样本本身表达形式一样的扩增正样本。下图更为直观理解样本的扩增情况,

(6)数据的存储结构
经过三次循环计算,可以得到 tcls, tbox, indices, anch四个存储数据的列表,列表的大小均为【3】,具体数值和形状如下陈述,第一次循环,
[[ 1.25000, 1.62500],[ 2.00000, 3.75000],[ 4.12500, 2.87500]],尺度1下的Anchor与标签框匹配,匹配的结果如下图所示,表示并没有找到合适的标签框

第二次循环,
[[ 1.87500, 3.81250],[ 3.87500, 2.81250],[ 3.68750, 7.43750]],尺度2下的Anchor与真实框匹配,结果如下图所示(包括扩增样本),匹配 6 个正样本。由于调试的时候,用的batch=1,所以img index均为0,
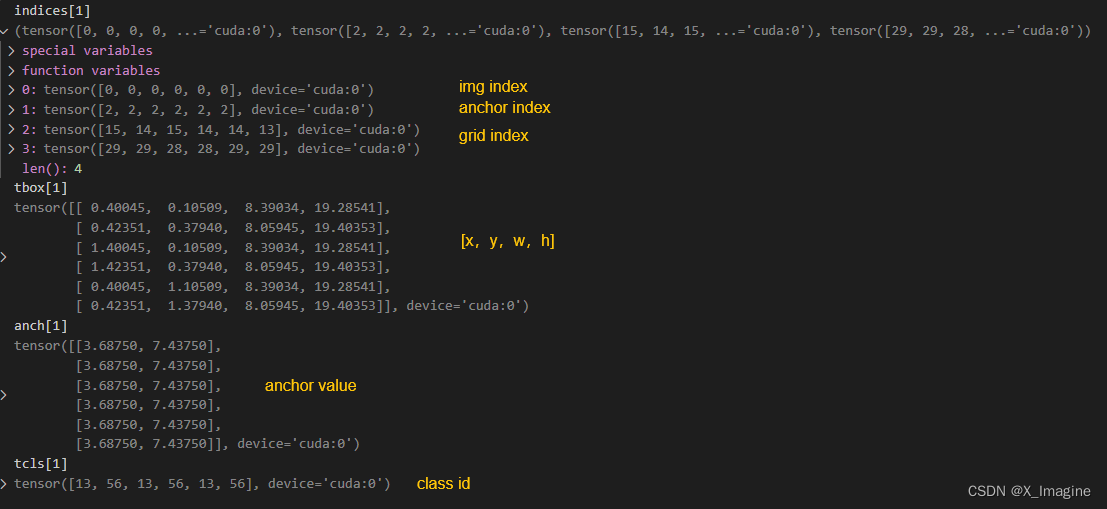
第三次循环,
[[ 3.62500, 2.81250],[ 4.87500, 6.18750],[11.65625, 10.18750]],尺度3下的Anchor与真实框匹配,结果如下图所示,匹配 【30】个正样本,
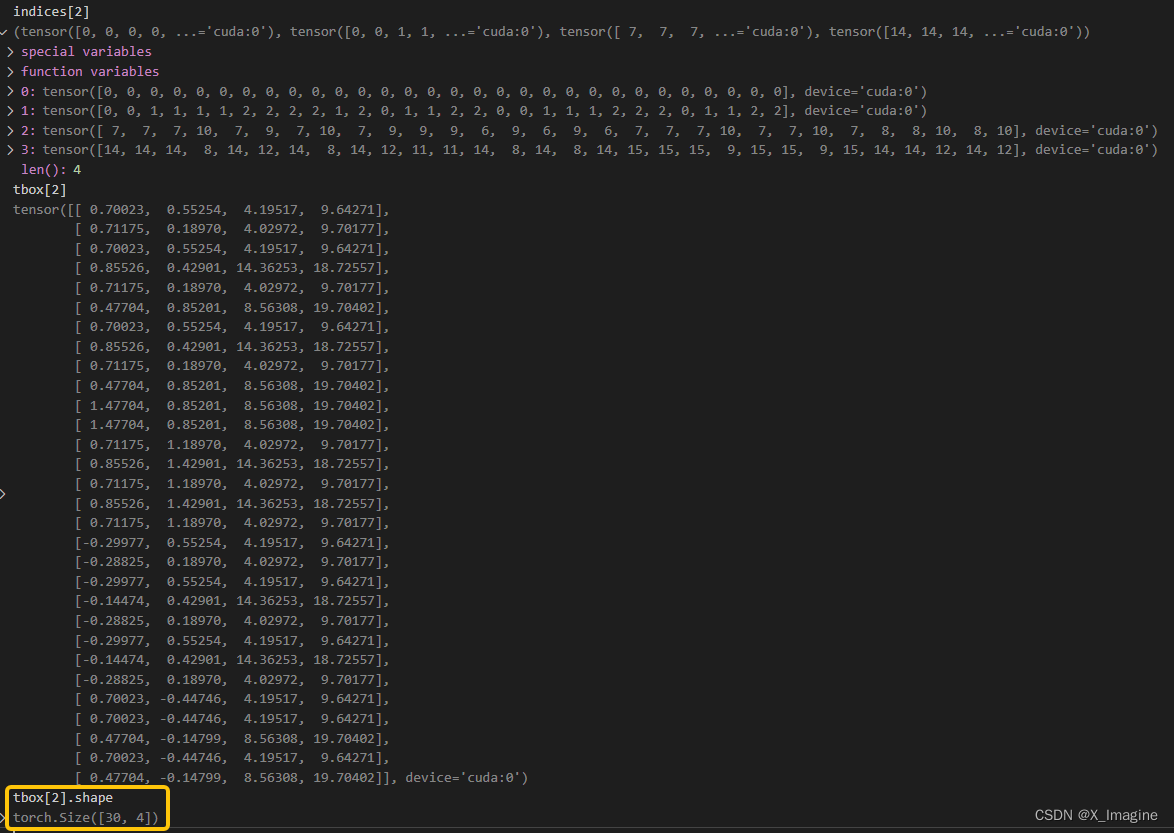

-
损失函数
(1) 整体概述
经过正样本扩增后,我们可以得到每一个Anchor尺度下匹配的标注框,通常数量是多于原始的标注框。在【扩增正样本,(6) 数据的存储结构】小节中,我们打印出了正样本数据的存储结构。网络的三层输出形状如下,
【1,3,80,80,85】
【1,3,40,40,85】
【1,3,20,20,85】
分类损失:类别的损失,只计算正样本,使用二元交叉熵损失函数;
定位损失:边框的损失,只计算正样本,使用CIOU作为损失函数;
置信度损失:衡量一个grid内存在目标的概率【0~1】,正样本和负样本都计算置信度,只是计算时的标签不一样,负样本是0,正样本的是CIOU的值;损失函数计算的核心代码结构如下所示,依次处理网络输出的每一层,最后将损失汇总求和(仔细阅读注释内容),
# Losses,网络输出层为三层,所以循环三次,依次计算损失 for i, pi in enumerate(p): # layer index, layer predictions b, a, gj, gi = indices[i] # image, anchor, gridy, gridx tobj = torch.zeros(pi.shape[:4], dtype=pi.dtype, device=self.device) # target obj n = b.shape[0] # number of targets if n: # 正样本数量,没有正样本是不进行下面的损失相关的计算 """ 省略代码,取出对应位置的预测数据 """ # Regression """ 省略代码,计算定位损失 """ # Objectness """ 计算IOU,用于后面计算置信度损失 """ # Classification """ 省略代码,生成one-hot标签,计算分类损失 """ # 即使没有正样本,仍需计算置信度损失, obji = self.BCEobj(pi[..., 4], tobj) # 为了改善不同样本的识别难度,每一层的置信度权重系数是不一样的【4,1,0.4】 lobj += obji * self.balance[i] # obj loss if self.autobalance: self.balance[i] = self.balance[i] * 0.9999 + 0.0001 / obji.detach().item() # 给每一个损失添加权重 if self.autobalance: self.balance = [x / self.balance[self.ssi] for x in self.balance] lbox *= self.hyp['box'] lobj *= self.hyp['obj'] lcls *= self.hyp['cls'] bs = tobj.shape[0] # batch size return (lbox + lobj + lcls) * bs, torch.cat((lbox, lobj, lcls)).detach()(2) 第一次循环
P3层的网络输出为【1,3,80,80,85】,而该层对应的正样本数量为【0】。此时不需要计算分类损失和定位损失,但是需要计算置信度损失。此时的二元交叉熵损失函数的标签是提前初始化为全零的矩阵【tobj】,其大小是与该层输出特征图的大小是一致的,每一个grid预测【3】个预测框,所以形状为 [1, 3, 80, 80]。# 即使没有正样本,仍需计算置信度损失, obji = self.BCEobj(pi[..., 4], tobj) # tobj 的形状为:torch.Size([1, 3, 80, 80]) # pi[..., 4]的形状为:torch.Size([1, 3, 80, 80]) # 为了改善不同尺寸目标的识别难度,每一层的置信度权重系数是不一样的【4,1,0.4】 lobj += obji * self.balance[i] # obj loss上述代码使用的是二元交叉熵损失函数计算,并且合并了sigmoid函数。针对不同的层,置信度损失分别赋予不同的权重,计算的结果如下,

(3) 第二次循环
首先,取出提前保存的索引值。具体的值可以参考【扩增正样本,(6) 数据的存储结构】小节中第二次循环的打印结果。此时会再次初始化【tobj】为全零矩阵,形状为 torch.Size([1, 3, 40, 40]),与当前层输出特征图大小保持一致。b, a, gj, gi = indices[i] # image, anchor, gridy, gridx tobj = torch.zeros(pi.shape[:4], dtype=pi.dtype, device=self.device) # target obj其次,从预测的数据中取出有效数据。此时正样本数量【n=6】,然后从预测结果【pi】中取出有效的数据,所谓有效的数据,表示这个位置有正样本,a,b,gj,gi 就是正样本所在位置的索引。
if n: # pxy, pwh, _, pcls = pi[b, a, gj, gi].tensor_split((2, 4, 5), dim=1) # faster, requires torch 1.8.0 pxy, pwh, _, pcls = pi[b, a, gj, gi].split((2, 2, 1, self.nc), 1) # target-subset of predictions那么,如何从高维Tensor中取数据?如下图所示,依据【b】可以定位到batch的哪一个大的块,【a】可以定位到哪一个anchor块,【gj,gi】定位具体grid,

然后,计算损失。
定位损失:pxy与pwh的计算方式与YOLO-V3不一样,边框损失使用CIOU,# Regression pxy = pxy.sigmoid() * 2 - 0.5 pwh =(pwh.sigmoid() * 2) ** 2 * anchors[i] pbox = torch.cat((pxy, pwh),1) # predicted box iou = bbox_iou(pbox, tbox[i], CIoU=True).squeeze() # iou(prediction, target) lbox += (1.0 - iou).mean() # iou loss置信度损失:这里用IOU值给【tobj】赋予置信度值,也是后面计算置信度损失的标签值,L7行代码如下,
iou.detach().clamp(0).type(tobj.dtype) if self.sort_obj_iou: j = iou.argsort() b, a, gj, gi, iou = b[j], a[j], gj[j], gi[j], iou[j] if self.gr < 1: iou = (1.0 - self.gr) + self.gr * iou tobj[b, a, gj, gi] = iou # iou ratio分类损失:用self.cn=0初始化t,形状为 torch.Size([6, 80]),代码L5行将类别id作为索引值,给【t】指定位置赋值为【1】,相当于制作【one-hot】标签。L6行代码调用二元交叉熵函数计算分类损失,
# Classification if self.nc > 1: # cls loss (only if multiple classes) # 初始化0矩阵 t = torch.full_like(pcls, self.cn, device=self.device) # targets t[range(n), tcls[i]] = self.cp lcls += self.BCEcls(pcls, t) # BCE上述过程完成了【正样本】的损失计算。下面继续计算置信度损失,【tobj】既有正样本又有负样本,正样本标签为【iou】值,负样本标签为【0】,
obji = self.BCEobj(pi[..., 4], tobj) lobj += obji * self.balance[i] # obj loss(4) 第三次循环
与第二次类似,略。(5) 最终结果
三部分损失的权重是不太一样的,box=0.05,obj=1,cls=0.5. 最终的损失是三部分之和,并且乘以batch_size,代码如下lbox *= self.hyp['box'] lobj *= self.hyp['obj'] lcls *= self.hyp['cls'] bs = tobj.shape[0] # batch size return (lbox + lobj + lcls) * bs, torch.cat((lbox, lobj,lcls)).detach()






](https://img-blog.csdnimg.cn/img_convert/e6676e08e1a2e253e9f6e3de05cd34c8.png)