N皇后问题-leetcode51-java回溯解+详细优化过程

news2024/10/6 6:50:59

说明：问题描述来源leetcode

一、问题描述：

51. N 皇后

难度困难1592

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

img

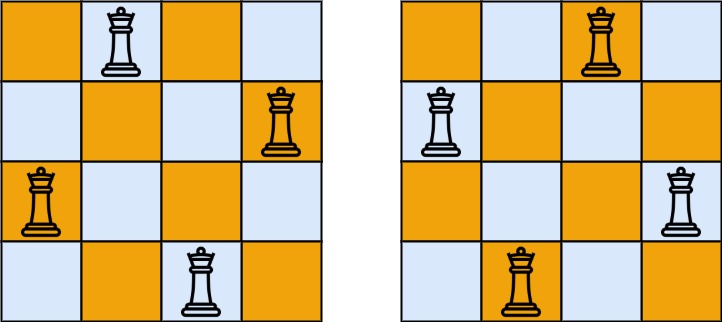
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

  • 1 <= n <= 9

二、题解：

做题过程：

题解1：

class Solution {
    List<List<String>> res = new LinkedList<>();
    char[][] chars ;
    private int n;

    public List<List<String>> solveNQueens(int n) {
        chars= new char[n][n];
        this.n = n;
        backTracking(0,0,0);
        return res;
    }

    private void backTracking(int row, int column,int count) {
        if (count == n){
            // 说明已经达到了不会相互攻击的n皇后,可以通过char获取一个结果
            addToRes();
            return;
        }
        for (int i = row; i < n; i++) {
            for (int j = column; j < n; j++) {
                if (chars[i][j] == 0){
                    char[][] arrays = getNewArrays();
                    doIAndJ(i,j);
                    count++;
                    backTracking(i + 1,0,count);
                    count--;
                    chars = arrays;

                }
            }
        }
    }

    private void addToRes() {
        List<String> list = new ArrayList<>();

        for (int i = 0; i < chars.length; i++) {
            String s = String.valueOf(chars[i]);
            list.add(s);
        }
        res.add(new ArrayList<>(list));

    }

    private char[][] getNewArrays() {
        char[][] result = new char[n][n];
        for (int i = 0; i < chars.length; i++) {
            for (int j = 0; j < chars[i].length; j++) {
                result[i][j] = chars[i][j];
            }
        }

        return result;
    }

    private void doIAndJ(int row, int column) {
        chars[row][column] = 'Q';
        for (int i = 0; i < n; i++) {
            if (chars[row][i] == 0) chars[row][i] = '.'; 
            
            if (chars[i][column] == 0) chars[i][column] = '.'; 
            
            if (column - i >= 0){//左边
                if (row - i >=0 && chars[row - i][column - i] == 0) chars[row - i][column - i] = '.';//左上 
                if (row + i < n && chars[row + i][column - i] == 0) chars[row + i][column - i] = '.';//左下 
            }
            
            if (column + i < n){//右边
                if (row - i >=0 && chars[row - i][column + i] == 0) chars[row - i][column + i] = '.';//左上 
                if (row + i < n && chars[row + i][column + i] == 0) chars[row + i][column + i] = '.';//左下 
            }
            
            
        }
    }
}

这个可以通过n为4的情况

后面这个题解通过了！！！

居然通过了哈哈！

还以为会超出时间复杂度。

还可以继续优化：

题解2：

再分析：

每一行必定会有一个皇后。

为什么？我们拆解这句话应该是等价于：每一行最多只可以有一个皇后，最少也是只有一个皇后。

先证明前半部分每一行最多只可以有一个皇后，①反证法：假如存在一行有2个皇后，那么不就和题目所说的同一行的皇后会相互攻击的条件所矛盾了吗？

再证明后半部分最少也是只有一个皇后,②反证法：假如最少是0个，那么存在一行没有皇后，那么肯定会有某一行会有多个皇后，这不就又回到①了吗

因此每一行必定有一个皇后。也不知道证明得够不够说服力，目前就感觉证明得没什么问题。

那么当我们即将遍历到n+1行就退出即可。

相应的，根据对称性，每一列也必定会存在一个皇后。

找到了这个条件，我们可以改造下：

class Solution {
    List<List<String>> res = new LinkedList<>();
    char[][] chars;
    private int n;

    public List<List<String>> solveNQueens(int n) {
        chars = new char[n][n];
        this.n = n;
        backTracking(0);
        return res;
    }

    private void backTracking(int row) {
        if (row == n) {
            // 说明已经达到了不会相互攻击的n皇后,可以通过char获取一个结果
            addToRes();
            return;
        }
        for (int i = 0; i < n; i++) {//对于每一列
            if (chars[row][i] == 0) {
                char[][] arrays = getNewArrays();
                doIAndJ(row,i);
                backTracking(row + 1);
                chars = arrays;
            }
        }
    }


    private void addToRes() {
        List<String> list = new ArrayList<>();

        for (int i = 0; i < chars.length; i++) {
            String s = String.valueOf(chars[i]);
            list.add(s);
        }
        res.add(new ArrayList<>(list));

    }

    private char[][] getNewArrays() {
        char[][] result = new char[n][n];
        for (int i = 0; i < chars.length; i++) {
            for (int j = 0; j < chars[i].length; j++) {
                result[i][j] = chars[i][j];
            }
        }

        return result;
    }

    private void doIAndJ(int row, int column) {
        chars[row][column] = 'Q';
        for (int i = 0; i < n; i++) {
            if (chars[row][i] == 0) chars[row][i] = '.';

            if (chars[i][column] == 0) chars[i][column] = '.';

            if (column - i >= 0) {//左边
                if (row - i >= 0 && chars[row - i][column - i] == 0) chars[row - i][column - i] = '.';//左上 
                if (row + i < n && chars[row + i][column - i] == 0) chars[row + i][column - i] = '.';//左下 
            }

            if (column + i < n) {//右边
                if (row - i >= 0 && chars[row - i][column + i] == 0) chars[row - i][column + i] = '.';//左上 
                if (row + i < n && chars[row + i][column + i] == 0) chars[row + i][column + i] = '.';//左下 
            }


        }
    }
}

end

这里的效率较之题解1已经提高了很多了，剩下的应该是对数据的处理的部分的优化了。

而题解1和题解2相比较，题解1走多了什么步骤呢？题解1有2层循环，我们可以设想当第一层递归遍历到第二行的chars数组时，是不是已经算是找到了所有结果了呢？

事实上按照推理是这样的，当第一行全部遍历后已经是找到所有的结果了，而其他的递归也存在遍历第二次的场景。

也就是当那一行确定后，再遍历到下一行进行递归时就已经出现了重复了，不行可以改一下题解1的代码，让它每次递归都不走下一行的遍历：

class Solution {
List<List<String>> res = new LinkedList<>();
    char[][] chars ;
    private int n;

    public List<List<String>> solveNQueens(int n) {
        chars= new char[n][n];
        this.n = n;
        backTracking(0,0,0);
        return res;
    }

    private void backTracking(int row, int column,int count) {
        if (count == n){
            // 说明已经达到了不会相互攻击的n皇后,可以通过char获取一个结果
            addToRes();
            return;
        }
        for (int i = row; i < n; i++) {
            for (int j = column; j < n; j++) {
                if (chars[i][j] == 0){
                    char[][] arrays = getNewArrays();
                    doIAndJ(i,j);
                    count++;
                    backTracking(i + 1,0,count);
                    count--;
                    chars = arrays;

                }
            }
            break;
        }
    }

    private void addToRes() {
        List<String> list = new ArrayList<>();

        for (int i = 0; i < chars.length; i++) {
            String s = String.valueOf(chars[i]);
            list.add(s);
        }
        res.add(new ArrayList<>(list));

    }

    private char[][] getNewArrays() {
        char[][] result = new char[n][n];
        for (int i = 0; i < chars.length; i++) {
            for (int j = 0; j < chars[i].length; j++) {
                result[i][j] = chars[i][j];
            }
        }

        return result;
    }

    private void doIAndJ(int row, int column) {
        chars[row][column] = 'Q';
        for (int i = 0; i < n; i++) {
            if (chars[row][i] == 0) chars[row][i] = '.';

            if (chars[i][column] == 0) chars[i][column] = '.';

            if (column - i >= 0){//左边
                if (row - i >=0 && chars[row - i][column - i] == 0) chars[row - i][column - i] = '.';//左上
                if (row + i < n && chars[row + i][column - i] == 0) chars[row + i][column - i] = '.';//左下
            }

            if (column + i < n){//右边
                if (row - i >=0 && chars[row - i][column + i] == 0) chars[row - i][column + i] = '.';//左上
                if (row + i < n && chars[row + i][column + i] == 0) chars[row + i][column + i] = '.';//左下
            }


        }
    }
}

这里和题解1的区别就是只完成内部的一层遍历就break了，无法继续走下面的行的遍历，效率和题解2几乎一样。

我们剩下的就对题解2进行优化数据处理就可以了：

但是本题解2的数据处理部分很难处理，这里对数据的操作实在是够多了的，比如getNewArrays这个函数每次都要创建和修改，其他的也是，总之很难修改了，是因为选定了默认（数值表示为0）的char作为判断条件.

可以换另一种思路，

比如说让是否为目标值作为判断条件。

题解3：

下面是替换了要判断的目标值，同时对数据的操作也减少了，不需要很多次地进行数组的创建

class Solution {
    List<List<String>> res = new LinkedList<>();
    char[][] chars;
    private int n;

    public List<List<String>> solveNQueens(int n) {
        chars = new char[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(chars[i],'.');
        }
        this.n = n;
        backTracking(0);
        return res;
    }

    private void backTracking(int row) {
        if (row == n) {
            // 说明已经达到了不会相互攻击的n皇后,可以通过char获取一个结果
            addToRes();
            return;
        }
        for (int i = 0; i < n; i++) {//对于每一列
            if (!isExistQ(row,i)){
                chars[row][i] = 'Q';
                backTracking(row + 1);
                chars[row][i] = '.';
            }
        }
    }

    private boolean isExistQ(int row, int column) {
        for (int i = 0; i < n; i++) {//判断列
            if ( chars[i][column] == 'Q') return true;

        }
        for (int i = 1; i < n; i++) {
            if (column - i >= 0) {//左边
                if (row - i >= 0 && chars[row - i][column - i] == 'Q') return true;//左上
                if (row + i < n && chars[row + i][column - i] == 'Q') return true;//左下
            }

            if (column + i < n) {//右边
                if (row - i >= 0 && chars[row - i][column + i] == 'Q') return true;//左上
                if (row + i < n && chars[row + i][column + i] == 'Q') return true;//左下
            }
        }
        return false;
    }


    private void addToRes() {
        List<String> list = new ArrayList<>();

        for (int i = 0; i < chars.length; i++) {
            String s = String.valueOf(chars[i]);
            list.add(s);
        }
        res.add(new ArrayList<>(list));

    }
}

但是还是不够！到底是哪里出错了呢，然后思考一下：

再来剪枝操作一下终于！！！

题解4：

对于斜边的操作其实只需要对左上角、右上角进行查询是否有目标值Q就可以了

class Solution {
    List<List<String>> res = new LinkedList<>();

    public List<List<String>> solveNQueens(int n) {
        char[][] chars = new char[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(chars[i], '.');
        }
        backTracking(chars, n, 0);
        return res;
    }

    private void backTracking(char[][] chars, int n, int row) {
        if (row == n) {
            // 说明已经达到了不会相互攻击的n皇后,可以通过char获取一个结果
            addToRes(chars);
            return;
        }
        for (int i = 0; i < n; i++) {//对于每一列
            if (!isExistQ(chars, n, row, i)) {
                chars[row][i] = 'Q';
                backTracking(chars, n, row + 1);
                chars[row][i] = '.';
            }
        }
    }

    private boolean isExistQ(char[][] chars, int n, int row, int column) {
        for (int i = 0; i < n; i++) {//判断列
            if (chars[i][column] == 'Q') return true;

        }

        for (int i = column - 1, j = 1; i >=0 && row - j >= 0; i--, j++) {
            if (chars[row - j][i] == 'Q') return true;//左上
        }
        
        for (int i = column + 1, j = 1; i < n && row - j >= 0; i++, j++) {
            if (chars[row - j][i] == 'Q') return true;//左上
        }

        return false;
    }


    private void addToRes(char[][] chars) {
        List<String> list = new ArrayList<>();

        for (int i = 0; i < chars.length; i++) {
            String s = String.valueOf(chars[i]);
            list.add(s);
        }
        res.add(new ArrayList<>(list));

    }
}

这个就成功优化到了2ms，而这样子实际上还是可以优化的，对于列的目标值Q的查询直接剔除在下方的那些就可以了

也就是对isExistQ函数的列操作进行稍作改变：

class Solution {
    List<List<String>> res = new LinkedList<>();

    public List<List<String>> solveNQueens(int n) {
        char[][] chars = new char[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(chars[i], '.');
        }
        backTracking(chars, n, 0);
        return res;
    }

    private void backTracking(char[][] chars, int n, int row) {
        if (row == n) {
            // 说明已经达到了不会相互攻击的n皇后,可以通过char获取一个结果
            addToRes(chars);
            return;
        }
        for (int i = 0; i < n; i++) {//对于每一列
            if (!isExistQ(chars, n, row, i)) {
                chars[row][i] = 'Q';
                backTracking(chars, n, row + 1);
                chars[row][i] = '.';
            }
        }
    }

    private boolean isExistQ(char[][] chars, int n, int row, int column) {
        for (int i = 0; i < row; i++) {//判断列
            if (chars[i][column] == 'Q') return true;

        }

        for (int i = column - 1, j = 1; i >=0 && row - j >= 0; i--, j++) {
            if (chars[row - j][i] == 'Q') return true;//左上
        }
        
        for (int i = column + 1, j = 1; i < n && row - j >= 0; i++, j++) {
            if (chars[row - j][i] == 'Q') return true;//左上
        }

        return false;
    }


    private void addToRes(char[][] chars) {
        List<String> list = new ArrayList<>();

        for (int i = 0; i < chars.length; i++) {
            String s = String.valueOf(chars[i]);
            list.add(s);
        }
        res.add(new ArrayList<>(list));

    }
}

end

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/126777.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

实验八、直接耦合多级放大电路的调试

实验八、直接耦合多级放大电路的调试

一、题目 两级直接耦合放大电路的调试。 二、仿真电路 图1(a)所示电路为两级直接耦合放大电路&#xff0c;第一级为双端输入、单端输出差分放大电路&#xff0c;第二级为共射放大电路。 由于在分立元件中很难找到在任何温度下均具有完全相同特性的两只晶体管&#xff0c;因而…
阅读更多...
Active Directory 基础 —— 如何理解group的类型

Active Directory 基础 —— 如何理解group的类型

因为创建一个跨域的组，重新温习了一下最基本的AD知识，所谓温故而知新，把温习的结果整理了一下。AD里面的group类型从范围来说分为global, universal 和 local domain, 从类型来分分为security和distribution。后面的类型理解很容易，security就是纯粹用来权限访问的，而dist…
阅读更多...
Java实现FIFO、LRU、LFU、OPT四页面置换算法

Java实现FIFO、LRU、LFU、OPT四页面置换算法

题目要求 采用多道程序思想设计一个程序&#xff0c;模拟页存储管理地址变换的过程&#xff0c;可采用FIFO、LRU、LFU、OPT四页面置换算法。基本要求如下&#xff1a; 需要建立访问页表线程、访问快表线程、缺页中断处理线程、访问内存线程等&#xff0c;协同这些线程模拟完成…
阅读更多...
JDK17升级之路：JCE cannot authenticate the provider BC问题

JDK17升级之路：JCE cannot authenticate the provider BC问题

问题的产生 报错代码运行环境 JDK&#xff1a;Oracle JDK17 CentOS7.8 这个问题刚拿到比较棘手。原因是本地windows是OK的&#xff0c;centos上是不成功的&#xff0c;报了下面的错误&#xff1a; Caused by: java.lang.SecurityException: JCE cannot authenticate the provi…
阅读更多...
论文阅读 DeepGCNs: Can GCNs Go as Deep as CNNs?

论文阅读 DeepGCNs: Can GCNs Go as Deep as CNNs?

DeepGCNs: Can GCNs Go as Deep as CNNs?绪论1、介绍2、相关工作3、方法3.1、图神经网络的表针学习3.2、图神经网络的残差结构3.3、图神经网络的密集连接3.4、图神经网络的扩张性聚集绪论 CNN很强&#xff0c;但不能正确解决非欧几里得数据的问题&#xff0c;图卷积网络&…
阅读更多...
YOLO-V5 系列算法和代码解析（五）—— 损失函数

YOLO-V5 系列算法和代码解析（五）—— 损失函数

文章目录基本简介调试准备损失函数基本简介 损失函数是神经网络的重要组成部分&#xff0c;用于评估网络的预测值和真实值的差异度。根据偏差的大小&#xff0c;反向调整网络的训练参数&#xff0c;迭代优化使得损失尽量小&#xff0c;也就得到最优的网络参数。 调试准备 debu…
阅读更多...
Go-学生教务管理系统【无界面 / 离线版】（一）

Go-学生教务管理系统【无界面 / 离线版】（一）

【Go】学生教务管理系统&#xff08;无界面 / 离线版&#xff09;&#xff08;一&#xff09;Ⅰ. 程序说明一、博客日期二、引言Ⅱ. 版权声明Ⅲ. 开发环境一、开发配置二、开发工具Ⅳ. 效果演示一、工程结构&#xff08;一&#xff09;目录结构&#xff08;二&#xff09;目录说…
阅读更多...
【Ctfer训练计划】——(六)

【Ctfer训练计划】——(六)

作者名&#xff1a;Demo不是emo 主页面链接&#xff1a;主页传送门 创作初心&#xff1a;舞台再大&#xff0c;你不上台&#xff0c;永远是观众&#xff0c;没人会关心你努不努力&#xff0c;摔的痛不痛&#xff0c;他们只会看你最后站在什么位置&#xff0c;然后羡慕或鄙夷座…
阅读更多...
Springboot启动之自定义run方法

Springboot启动之自定义run方法

前言 之前分析的Springboot启动过程的源码分析中给自己留了一个扩展作业&#xff1a;执行自定义的run方法&#xff0c;此方法在B.7、调用运行器简单分析过&#xff0c;今天咱们就自定义一个Run方法试试。 一、实现自定义的run方法 由于java中的接口可以多实现&#xff0c;所以…
阅读更多...
IOS----TangramKit 布局框架

IOS----TangramKit 布局框架

文章目录系统结构CocoaPods安装举例下面一个应用场景:布局线性布局TGLinearLayout相对布局TGRelativeLayout框架布局TGFrameLayout表格布局TGTableLayout流式布局TGFlowLayout浮动布局TGFloatLayout路径布局MyPathLayoutgithub: https://github.com/youngsoft/TangramKit/blob…
阅读更多...
day32【代码随想录】回溯之N皇后、N皇后||、解数独、有效的数独

day32【代码随想录】回溯之N皇后、N皇后||、解数独、有效的数独

文章目录前言一、N皇后&#xff08;力扣51&#xff09;二、N皇后||&#xff08;力扣52&#xff09;三、解数独&#xff08;力扣37&#xff09;四、有效的数独&#xff08;力扣36&#xff09;前言 1、N皇后、 2、N皇后||、 3、解数独、 4、有效的数独 一、N皇后&#xff08;力扣…
阅读更多...
材料表征仪器：慢正电子束谱仪最全知识讲解

材料表征仪器：慢正电子束谱仪最全知识讲解

1 引言 21世纪科学的发展将是微观与宏观的相互渗透与密切结合。凝聚态物理、材料科学等的研究&#xff0c;将由现在的宏观统计方法&#xff08;包括宏观量子统计&#xff09;深入发展到物质的原子层次物性研究&#xff0c;微观粒子&#xff08;颗粒、孔隙&#xff09;的量子效…
阅读更多...
求最大公约数，求阶乘，求n个n相乘的末两位数（Python）

求最大公约数，求阶乘，求n个n相乘的末两位数（Python）

问题 AN: 41.求最大公约数 题目描述 对于求两个正整数m&#xff0c;n的最大公约数可以用do-while实现 输入 输入两个正整数m&#xff0c;n 输出 最大公约数 样例输入 1 2 样例输出 1 a,b map(int,input().split()) if a<b:a,b b,a#python很方便的交换操作 #适应判断不带…
阅读更多...
MySQL复制技术方案——异步复制配置

MySQL复制技术方案——异步复制配置

为MySQL服务器配置复制非常简单。但由于场景不同&#xff0c;基本的步骤还是有所差异。最基本的场景是新安装的主库和备库&#xff0c;总的来说分为以下几步∶ 1. 配置复制 为MySQL服务器配置复制非常简单。但由于场景不同&#xff0c;基本的步骤还是有所差异。最基本的场景是…
阅读更多...
HTML5 Canvas

HTML5 Canvas

文章目录HTML5 Canvas概述Canvas元素使用绘制直线画2条直线用直线画三角形用直线画矩形绘制矩形描边矩形填充矩形混合使用rect()清空矩形区域清空画布绘制多边形画箭头画正三角形绘制圆形HTML5 Canvas 概述 HTML5新增了一个Canvas元素&#xff0c;我们常说的Canvas技术&#…
阅读更多...
【LeetCode】填充每个节点的下一个右侧节点指针 [M]（二叉树遍历）

【LeetCode】填充每个节点的下一个右侧节点指针 [M]（二叉树遍历）

116. 填充每个节点的下一个右侧节点指针 - 力扣&#xff08;LeetCode&#xff09; 一、题目 给定一个 完美二叉树 &#xff0c;其所有叶子节点都在同一层&#xff0c;每个父节点都有两个子节点。二叉树定义如下&#xff1a; struct Node { int val; Node *left; Node *…
阅读更多...
通过webpack解决浏览器兼容问题

通过webpack解决浏览器兼容问题

前言 很多面试时都会问到关于浏览器兼容问题&#xff0c;正好最近在看webpack打包&#xff0c;那就在这里记录一下我们如何通过webpack来实现兼容。 需求 要知道我们到底需要兼容那些浏览器&#xff0c;在这里就需要用到browserlist来配置需要兼容的浏览器版本并告诉webpack…
阅读更多...
Jenkins自动部署项目

Jenkins自动部署项目

目录 1.安装插件 2.配置 本文只讲解通过插件来自动部署项目&#xff0c;Jenkins的安装可以看博主的另一篇文章&#xff0c;绝对保姆级&#xff0c;简洁丝滑的安装教程&#xff1a; jenkins下载安装__BugMan的博客-CSDN博客 1.安装插件 目前业内常用的解决方法是使用publish…
阅读更多...
程序员必备十大网站

程序员必备十大网站

窝窝整理了十大程序猿必备网站&#xff0c;涵盖了开源平台、搜索引擎、免费的精品课程&#xff0c;包括让你头疼的BUG、算法等。偷偷告诉你&#xff0c;还有帮你拿到心仪的 offer&#xff01; 一&#xff0c;海量的资源平台 十大网站榜首 &#xff1a;GitHub — 开发者极其重…
阅读更多...
图查询语言 nGQL 简明教程 vol.01 快速入门

图查询语言 nGQL 简明教程 vol.01 快速入门

本文旨在让新手快速了解 nGQL&#xff0c;掌握方向&#xff0c;之后可以脚踩在地上借助文档写出任何心中的 NebulaGraph 图查询。 视频 本教程的视频版在B站这里。 准备工作 在正式开始 nGQL 实操之前&#xff0c;记得先看过文档「快速入门流程」&#xff0c;部署、连接过 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023