前言

之前分析的Springboot启动过程的源码分析中给自己留了一个扩展作业：执行自定义的run方法，此方法在B.7、调用运行器简单分析过，今天咱们就自定义一个Run方法试试。

一、实现自定义的run方法

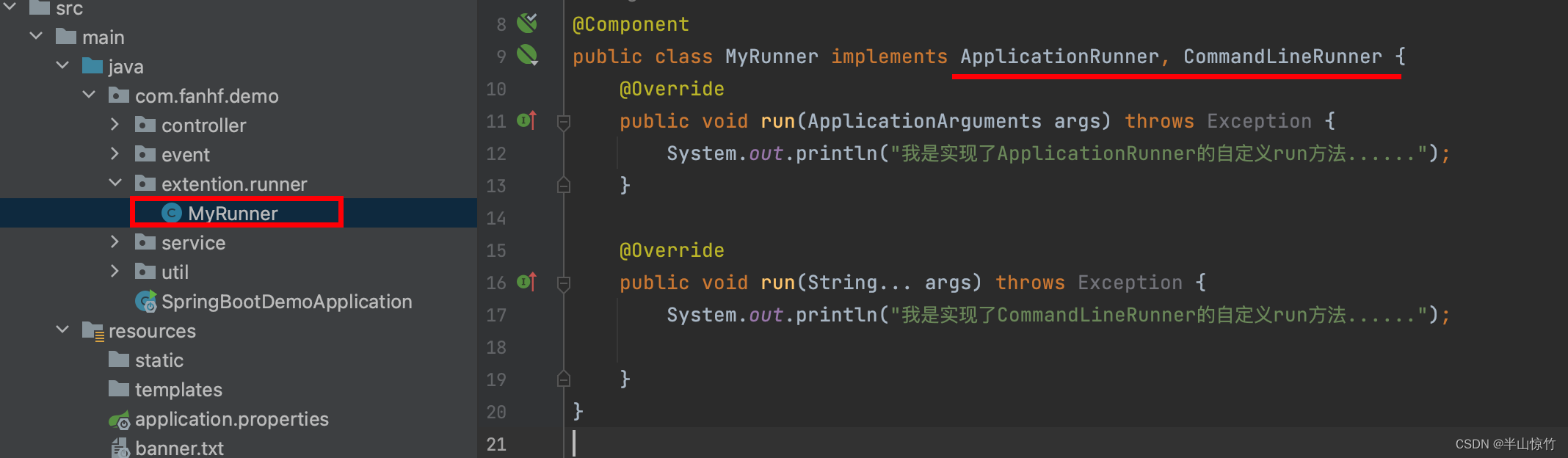
由于java中的接口可以多实现，所以我们一次性实现两个接口，重新两个接口的方法，可以看到两个接口的run方法中的入参是不一样的，但本质上都是参数，只不过ApplicationRunner把参数封装成了ApplicationArguments对象，而CommandLineRunner就是String的可变数组。
运行一下看看控制台是否执行了咱们的自定义的run方法：

在整个run方法启动完成之后，打印了我们重写了两个run方法中的日志。实现起来还是很简单的。

二、重温运行器源码

我们回看Springboot源码分析的调用运行器的方法：

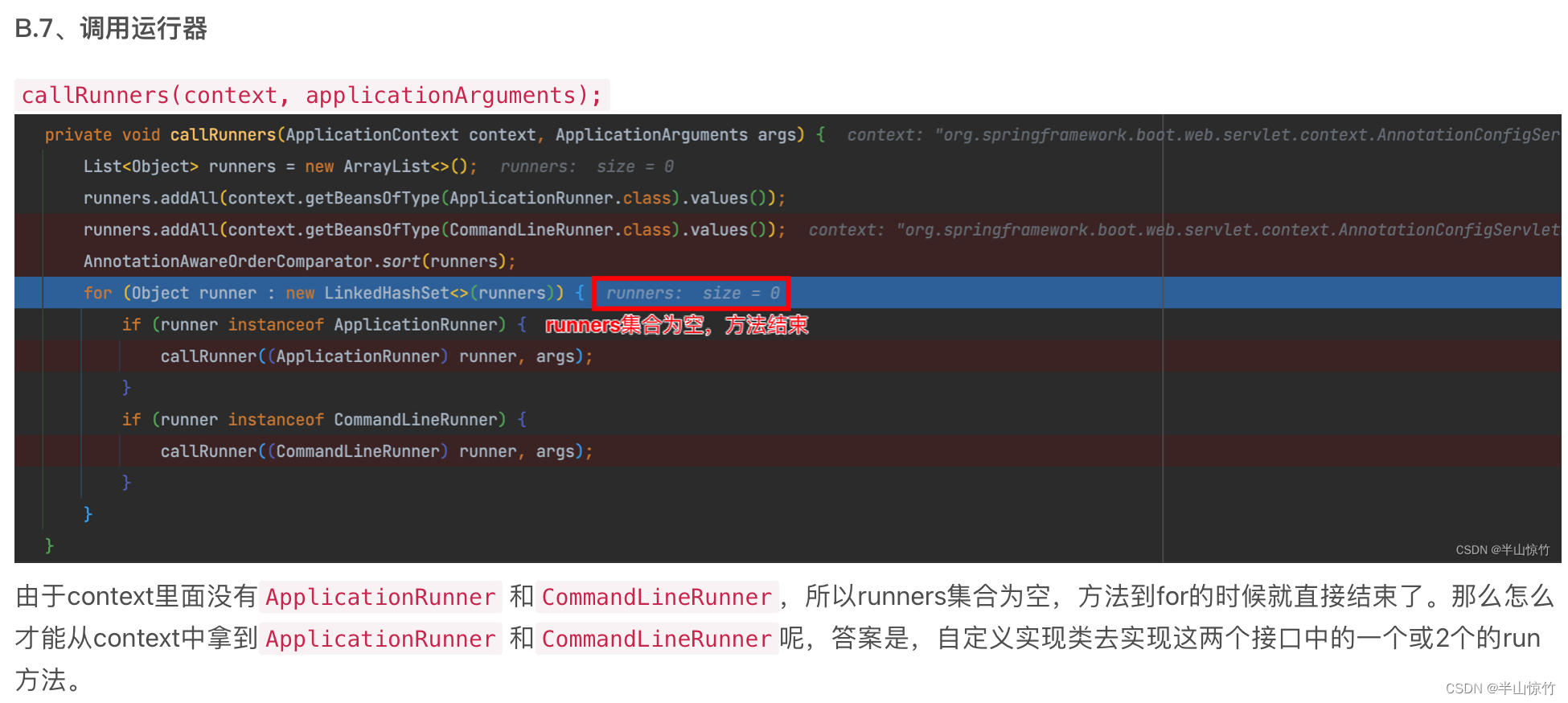
由于我们有了自定义的运行器，所以ApplicationRunner和CommandLineRunner就不是空的，我们重新进去看看，还是在run方法中的callRunners方法：

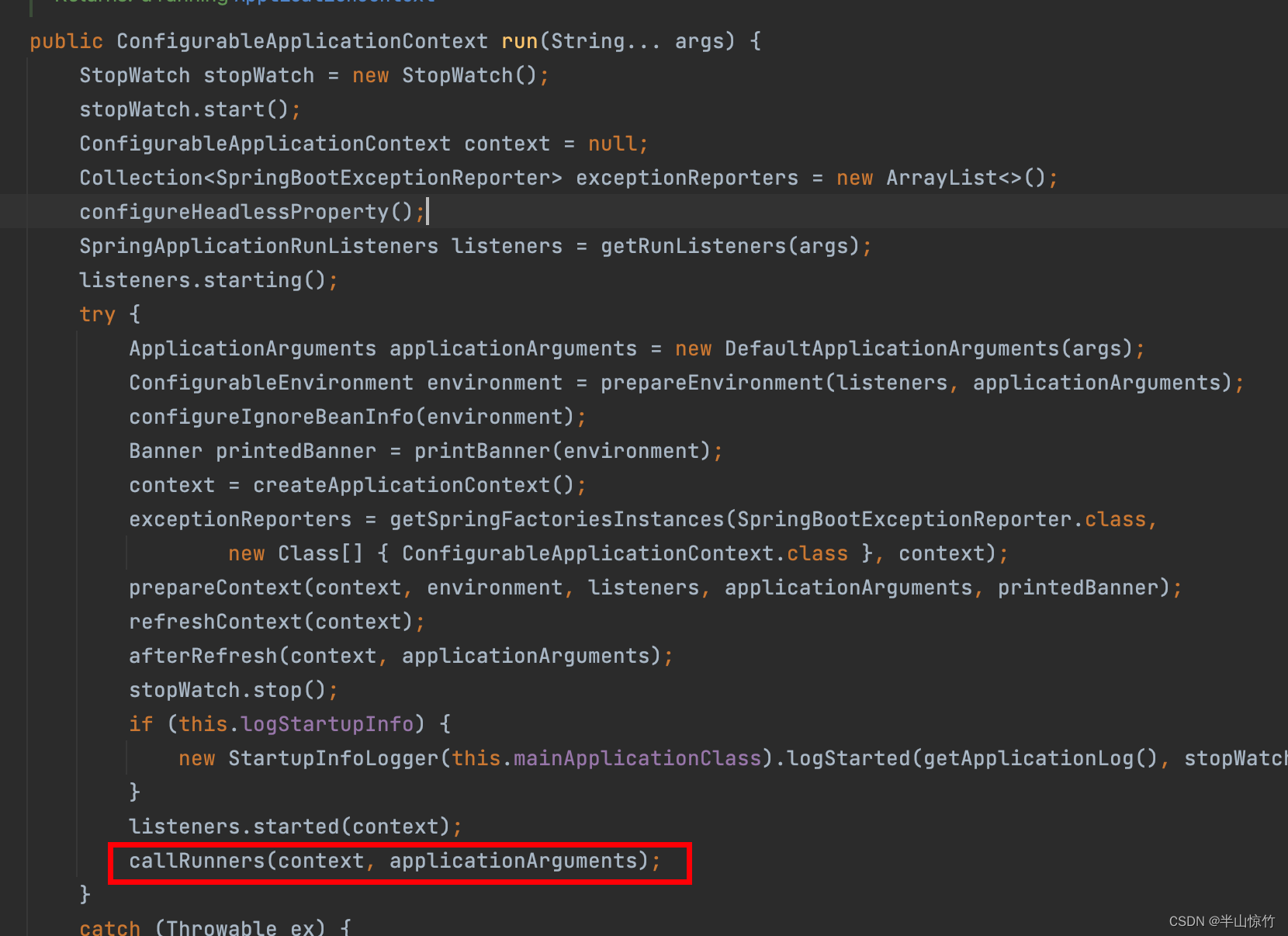
进入callRunners方法

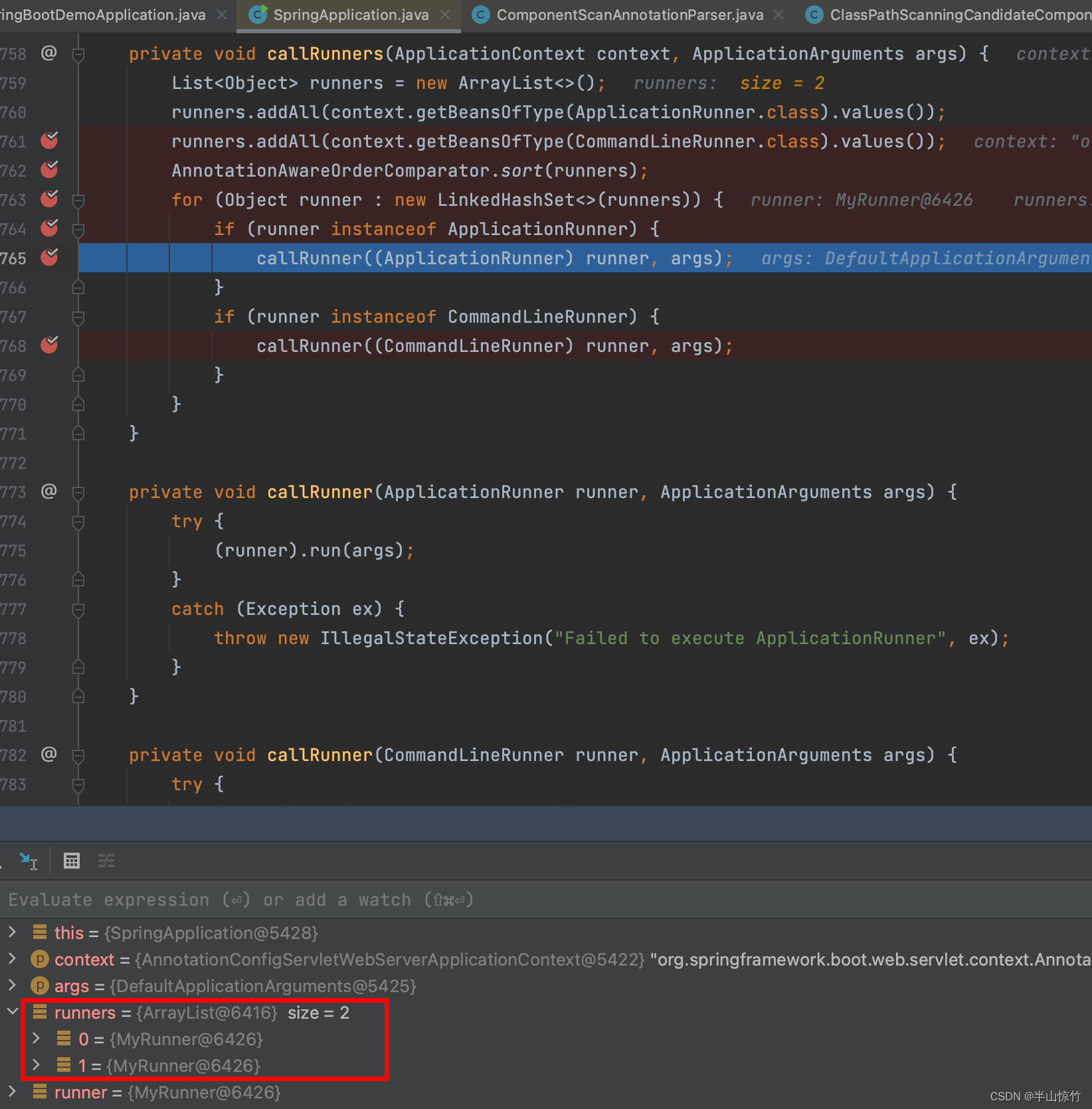
我们发现确实是有两个运行器，那这两个运行器是如何获取到的呢？这个就要往前看代码了。具体的代码分析就在Springboot启动过程的这篇文章的B.3.5、调用在上下文中注册为Bean的工厂处理器节中有个processConfigBeanDefinitions方法中的do-while循环中的parser.parse(candidates);方法，会对用户自定义的类进行解析加载后放到IOC容器中，我们这里看到的就是从IOC容器中取来用了。感兴趣的童鞋可以自己再debug回去看看哈~

---------------你知道的越多，不知道的越多-------------