一、题目

两级直接耦合放大电路的调试。

二、仿真电路

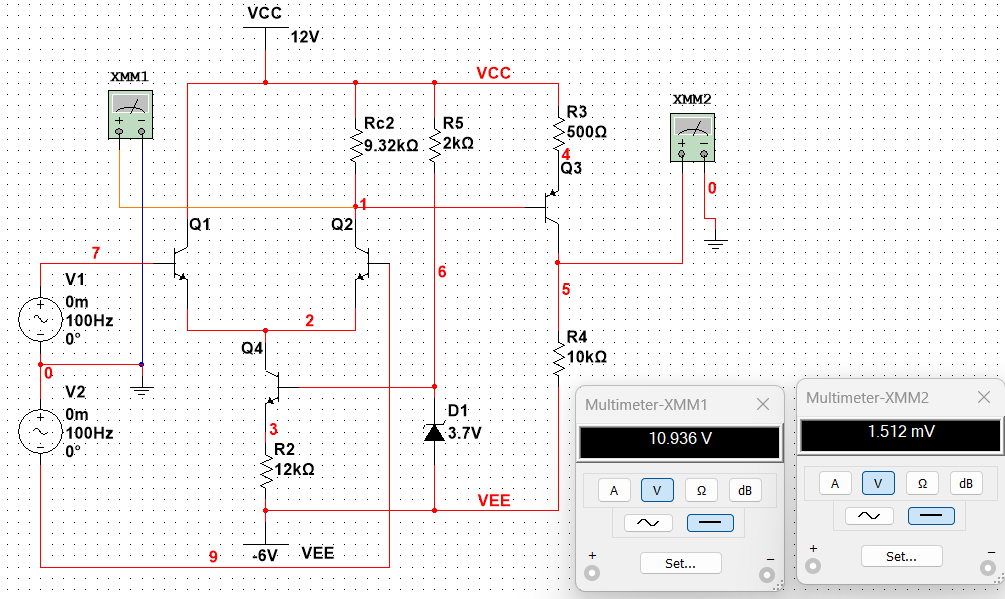
图1(a)所示电路为两级直接耦合放大电路，第一级为双端输入、单端输出差分放大电路，第二级为共射放大电路。
由于在分立元件中很难找到在任何温度下均具有完全相同特性的两只晶体管，因而也就很难实现共模抑制比很高的差分放大电路。在Multisim环境下可以做到两只晶体管特性基本相同。

三、仿真内容

（1）调整电路的静态工作点，使电路在输入电压为零时输出电压为零。用直流电压表测 $Q_2$、$Q_3$ 集电极静态电位，测试电路如图(a)所示。
（2）测试电路的电压放大倍数，输入电压是有效值为 2 mV 的正弦波，即峰值约为 2.829 mV，从示波器可读出输出电压的峰值，由此得电压放大倍数。测试方法如图(b)所示。
（3）测试电路的共模抑制比。加共模信号，从示波器可读出输出电压的峰值，得共模放大倍数，从而得到共模抑制比。测试电路如图($c$)所示。

$$(a)静态工作点的调试$$$$(b)电压放大倍数的测试$$$$图(c)共模放大倍数的测试$$$$图1两级直接耦合放大电路的测试$$

四、仿真结果

（1）静态工作点的调试结果如表1所示$$表1静态工作点的调试$$

$R_{c2}$/kΩ	10	9.8	9.7	9.6	9.5	9.4	9.3	9.32
$U_{CQ2}$/V	10.87	10.889	10.899	10.909	10.918	10.928	10.938	10.936
$U_{CQ3}$/mV	1207	853.392	676.398	499.136	321.621	143.87	-34.098	1.512

（2）电压放大倍数的测试结果如表2所示$$表2电压放大倍数的测试$$

输入差模信号电压峰值/mV	第一级输出电压峰值/mV	第一级差模放大倍数	第二级输出电压峰值/mV	第二级电压放大倍数	整个电路的电压放大倍数
2.829	51.827	18	-942.198	-18.180	-333.050

（3）共模放大倍数的测试如表3所示$$表3共模放大倍数的测试$$

输入共模信号电压峰值/mV	第一级输出电压峰值/pV	第二级输出电压峰值/pV	第一级共模放大倍数	整个电路的共模放大倍数	共模抑制比
141.421	12.822	-234.088	$9.1\times 10^{-11}$	$-1.66\times 10^{-9}$	$2\times 10^{11}$

五、结论

（1）由于直接耦合放大电路各级之间的静态工作点相互影响，一般情况下，应通过EDA软件调试各级的静态工作点，基本合适后再搭建电路，进行实际测试。
（2）当输入级为差分放大电路时，电路的电压放大倍数是指差模放大倍数。
（3）具有理想对称性的差分放大电路抑制共模信号的能力很强，因此以它作直接耦合多级放大电路的输入级可提高整个电路的共模抑制比。