本系列文章为浙江大学陈越、何钦铭数据结构学习笔记，前面文章链接如下：
数据结构基础：P1-基本概念
数据结构基础：P1-基本概念----编程作业01：最大子列和问题

---

一、题目描述

题目描述： 给定K个整数组成的序列 { N 1 , N 2 , . . . , N k } \{ {N_1},{N_2},...,{N_k}\} {N1​,N2​,...,Nk​} ，连续子列被定义为 { N i , N i + 1 , . . . , N j } \{ {N_i},{N_{i + 1}},...,{N_j}\} {Ni​,Ni+1​,...,Nj​}，其中 $1\le i\le j\le K$。最大子列和则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 }，其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序，计算给定整数序列的最大子列和，同时将最大子列的首尾元素打印出来。
输入格式：
输入第1行给出正整数 $K(\le 100000)$；第2行给出 $K$ 个整数，其间以空格分隔。
输出格式：
对于每个测试案例，在一行中输出最大的子列和、最大子序列的首尾元素。这些数字之间必须有一个空格，但在行末不能有多余的空格。如果最大子序列不是唯一的，则输出具有最小元素下标 $i$ 和 $j$ 的子序列（如示例案例所示）。如果这K个数字都是负数，那么它的最大和被定义为0，你应该输出整个序列的第一个和最后一个数字
输入样例：
10
-10 1 2 3 4 -5 -23 3 7 -21
输出样例：
10 1 4

二、代码实现

思路分析

本题是对前面最大子列和问题的扩展，需要我们额外输出最大子列的首尾元素。在线处理复杂度为$\mathrm{O}(\mathrm{N})$，因此我们采用该算法。
①遍历数组A，令当前子列加上A[i]。
②若当前子列和小于0，则说明A[i]无法为当前子列带来收益，于是抛弃A[i]，继续向后看：
----将当前子列和重置为0
----将i+1记录为临时首，后面更新时要用到
③若当前子列和不小于0且大于最大子列和，则说明A[i]可以为当前子列带来收益，于是更新：
----将最大子列和更新为当前子列和
----A[i]就是最大子列的尾
----将最大子列的首更新为前面记录的值

代码实现

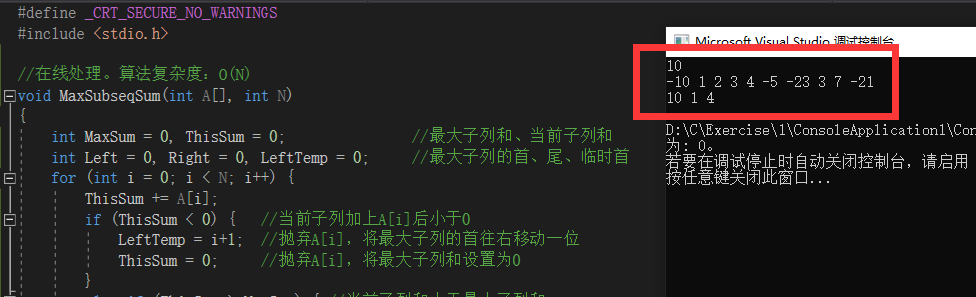
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>

//在线处理。算法复杂度：O(N)
void MaxSubseqSum(int A[], int N)
{
	int MaxSum = 0, ThisSum = 0;               //最大子列和、当前子列和
	int Left = 0, Right = 0, LeftTemp = 0;     //最大子列的首、尾、临时首
	for (int i = 0; i < N; i++) {
		ThisSum += A[i];     
		if (ThisSum < 0) {   //当前子列加上A[i]后小于0
			LeftTemp = i+1;  //抛弃A[i]，将最大子列的首往右移动一位
			ThisSum = 0;     //抛弃A[i]，将最大子列和设置为0
		}
		else if (ThisSum > MaxSum) { //当前子列和大于最大子列和
			MaxSum = ThisSum;        //更新最大子列和
			Right = i;				 //A[i]就是最大子列的尾
			Left = LeftTemp;         //更新最大子列的首
		}
	}
	if(MaxSum < 0)
		printf("0 %d %d\n", A[0], A[N-1]);
	else
		printf("%d %d %d\n", MaxSum, A[Left], A[Right]);
}

int main()
{
	int Array[10000];
	int n;
	scanf("%d", &n);
	for (int i = 0; i < n; i++) {
		scanf("%d", &Array[i]);
	}

	MaxSubseqSum(Array, n);

	return 0;
}

运行，输入测试样例，结果正确。