0 序言

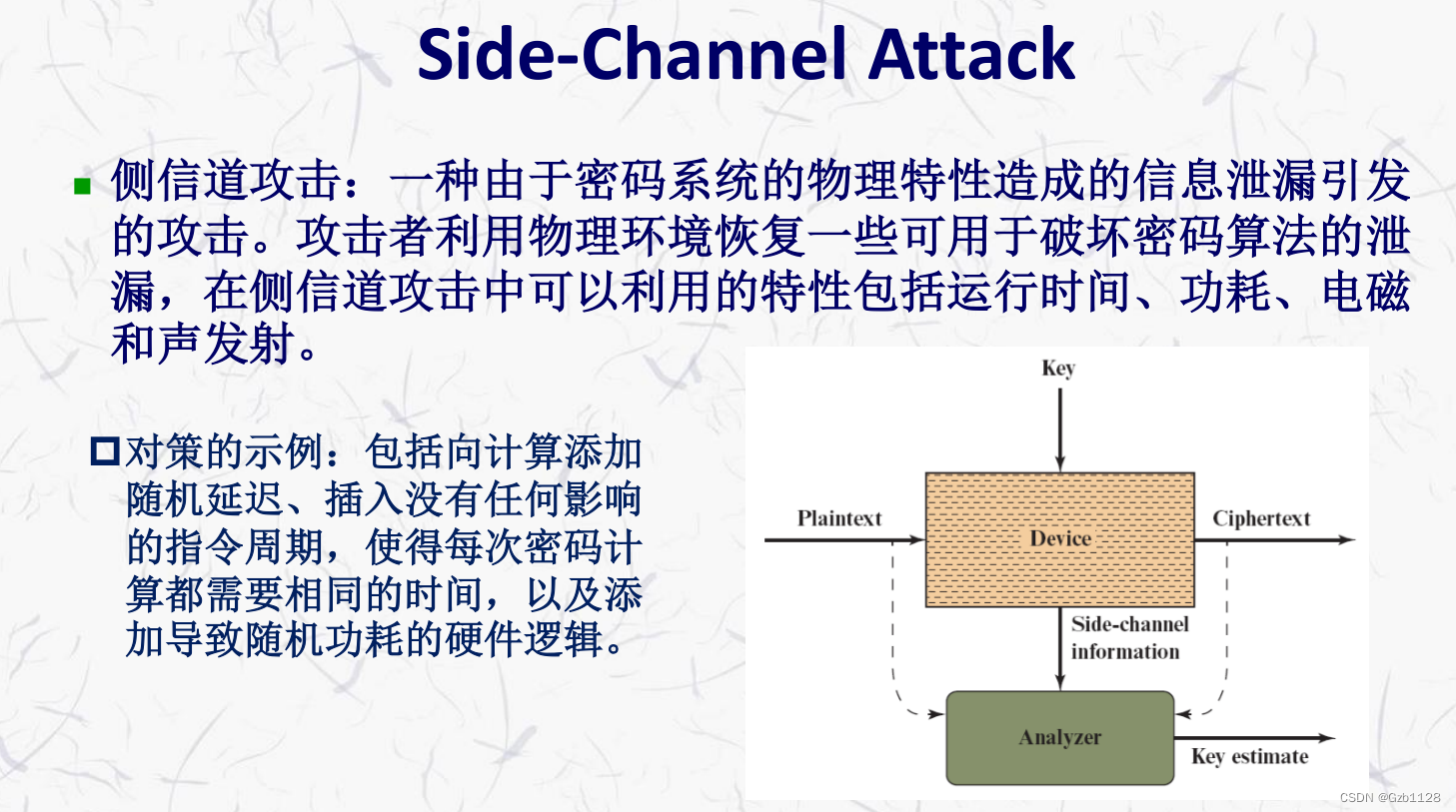
推荐系统中基于内容的协调过滤算法通过用户之间的相似性或者物品之间的相似性，通过相似性来为用户做决策和推荐；基于内容的协调过滤算法在实际生产环境中，User或Item的数据量非常大（百万级别），存储用户相似度矩阵或者物品相似度矩阵比较大，而User跟Item之间有反馈的数量又比较少，导致存在着数据稀疏和信息冗余大的缺陷，对稀疏数据的处理比较弱，而且头部效应比较明显，推荐更多都是偏向于热门的推荐，泛化能力比较差。

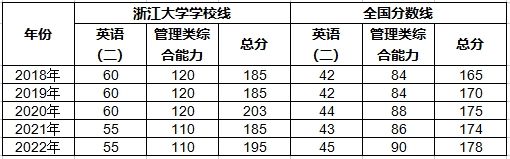
1 矩阵分解基本原理

矩阵分解基本原理：将$m\times n$的User-Item矩阵$D$分解为一个$m\times k$用户隐向量矩阵$U$和一个$n\times k$物品隐向量矩阵$V$相乘的形式，即$D_{m\times n}\approx V_{k\times n}^T{U}_{k\times m}$；其中，$m$为用户的数量，$n$为物品的数量，$k$为隐向量的维度。（如下图）

通过矩阵分解可以得到用户和物品都用$k$维隐向量的表达，每个商品可以用$1\times k$向量$q_i$表示，即$V=[q_0,q_1,...,q_n{]}^T$，每个用户可以用$1\times k$向量$p_u$表示，即$U=[p_0,p_1,...,p_m{]}^T$，则用户$u$与物品$i$的反馈得分为
$${\hat{r}}_{u,i}=q_i^T{p}_u$$

$k<<min(m,n)$，$k$的大小决定了隐向量表达能力的强弱，$k$的取值越小，隐向量包含的信息就越少，相对来讲泛化能力就越高；反之$k$取值越大，隐向量的表达能力越强，但泛化能力相对降低。

那么矩阵分解的推荐算法为：根据User-Item共现矩阵进行矩阵分解得到用户隐向量矩阵和物品隐向量矩阵，计算用户与未交互物品的预测得分，根据预测得分排序给用户推荐物品。

2 矩阵分解实现

矩阵求解的方法常见的方法有：
1）特征值分解
2）奇异值分解
3）梯度下降方法
4）交替最小二乘法
但是特征值分解与奇异值分解都不适合解决大规模稀疏矩阵分解的问题，因此，梯度下降法和最小二乘法成为了矩阵分解的主要方法。

2.1 梯度下降方法SGD

首先需要优化的目标函数为
$$loss=min\sum _{(u,i)\in K}(r_{ui}-q_i^T{p}_u{)}^2+\lambda (||p_u|{|}^2+||q_i|{|}^2)$$
然后对目标函数分别对$q_i$和$p_u$求偏导
$$\begin{gathered} q_i=q_i-2\gamma (r_{ui}-q_i^T{p}_u)p_u-2\lambda ||q_i|| \\ {p}_u=p_u-2\gamma (r_{ui}-q_i^T{p}_u)q_i-2\lambda ||p_u|| \end{gathered}$$
其中$\gamma$为学习率；
对$q_i$和$p_u$反复更新迭代，直到$loss$低于某个值或者迭代次数达到一定次数后，停止更新

2.2 交替最小二乘法ALS

ALS跟SGD都是需要优化目标函数$loss$，ALS先初始化固定其中一个变量$q_i$，然后通过对$p_u$求导反复迭代得到$p_u$的解，然后固定$p_u$，再对$q_i$求导反复迭代得到$q_i$的解；如此交替执行直到$loss$满足阈值条件或者到达迭代次数上限为止。

3 矩阵分解的优缺点

User和Item隐向量的生成过程其实是对共线矩阵进行全局拟合的过程。

优点：
1）泛化能力强，解决了数据稀疏的问题
2）空间复杂度低。不在需要用户相似度矩阵或者物品相似度矩阵，只需要存储用户和物品的隐向量，空间复杂度由 $O(M^2)$或者$O(N^2)$降低到$O(M\ast k+N\ast k)$级别。
缺点：
仅使用了物品和用户的行为特征，并没有使用用户、物品的自身属性和上下文特征，这让矩阵分解丧失了利用很多有效信息的机会

4 参考文献

[1] Matrix factorization techniques for recommender systems
[2] Netflix Update: Try This at Home
[3] 推荐系统中的矩阵分解技术
[4] 论文篇：Matrix Factorization Techniques for RS