一、红黑树
1、概念
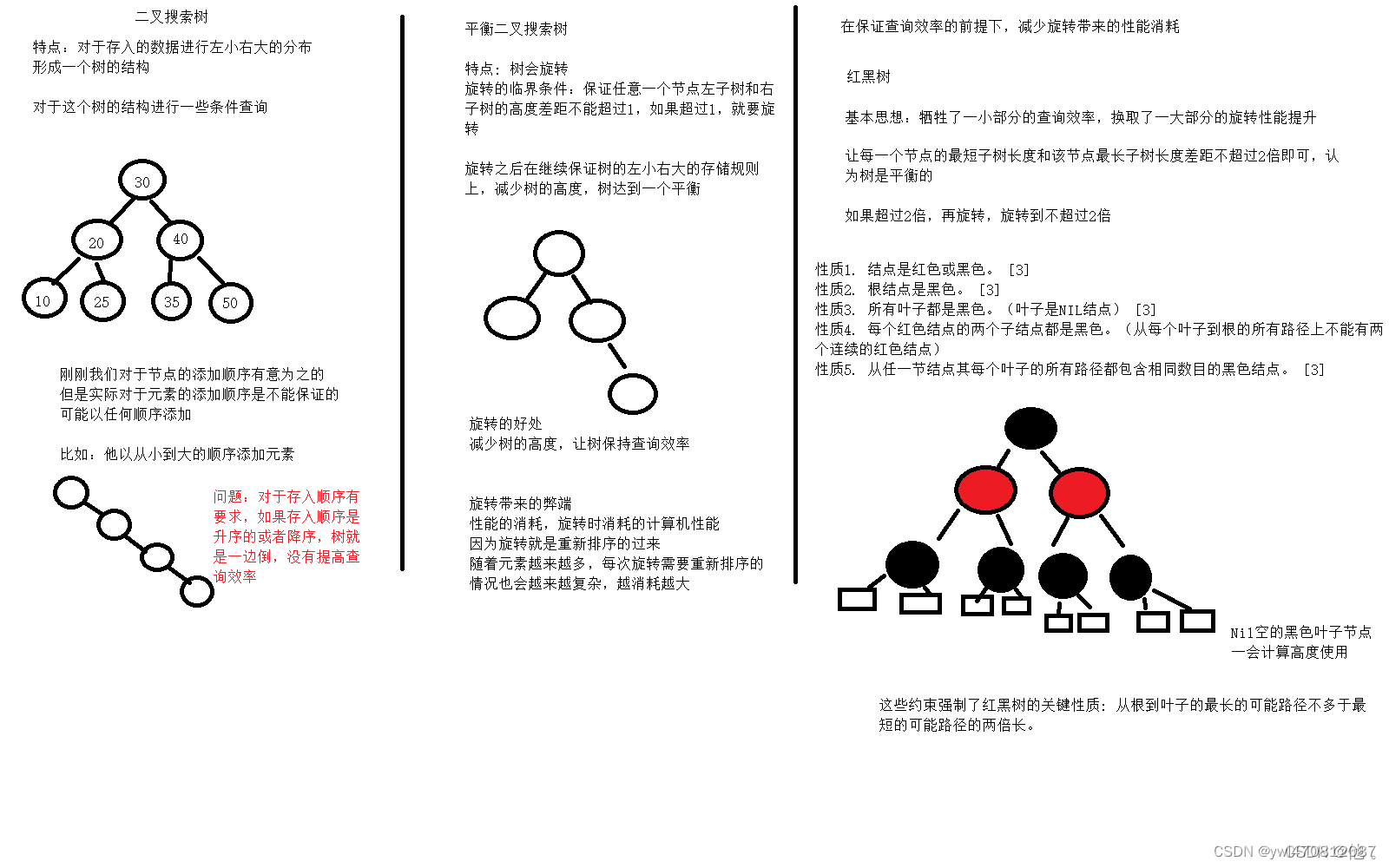
红黑树(Red Black Tree) 是一种自平衡二叉搜索树。它在每个结点上增加一个存储位表示结点的颜色,可以是 Red或 Black。
通过任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
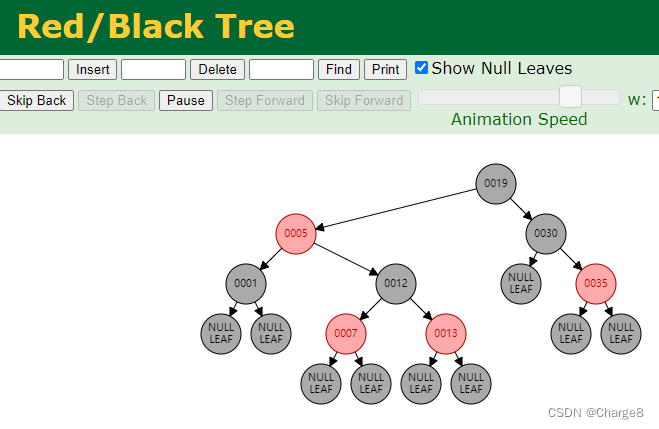
2、性质
红黑树的性质:
- 1)每个结点不是红色就是黑色。
- 2)根结点都是黑色。
- 3)所有叶子结点都是黑色。(叶子是黑色的空结点(NIL)),也就是说,叶子节点不存储数据。
- 4)每个红色结点的两个子结点都是黑色(从每个叶子到根的所有路径上不能有两个连续的红色结点)。也就是说不可能有连在一起的红色结点(黑色结点是可以的)。
- 5)从任一结点到其每个叶子结点的所有路径都包含相同数目的黑色结点。
3、红黑树的旋转
当我们在对红黑树进行插入和删除等操作时,对树做了修改,那么可能会违背红黑树的性质,因此,为了满足红黑树的性质,我们需要对结点进行改变颜色和旋转。
- 改变颜色:红变黑或者黑变红
- 旋转:又分为左旋和右旋
4、结点插入规则
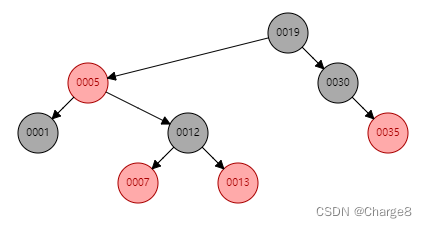
注意:插入的一定是红色。
我们插入结点[6]时,颜色变换和旋转规则如下:
1)颜色变换
改变颜色的情况:当前插入结点[6]的父亲是红色,且它的祖父结点的另一个子结点(叔叔结点)也是红色。:
- (1)把父结点设为黑色
- (2)把叔叔也设为黑色
- (3)把祖父(爷爷)也就是父亲的父亲设为红色。
- (4)把指针定义到祖父结点(爷爷)设为当前要操作的结点。
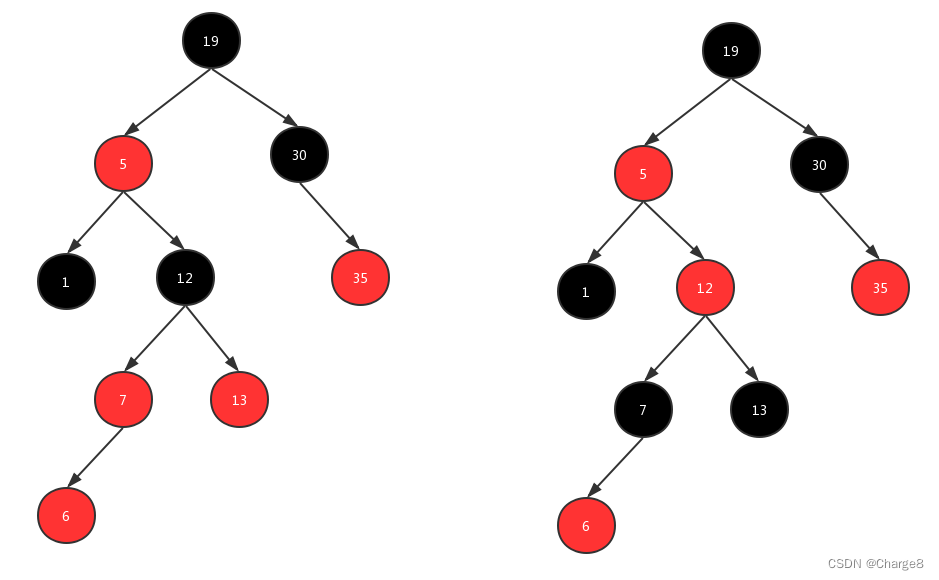
此时,当前指针:由 当前结点[6]变换为 爷爷结点[12]。
2)左旋
左旋:当前父结点是红色,叔叔是黑色的时候,且当前的结点是右子树。左旋
- (1)以父结点[5]作为左旋。
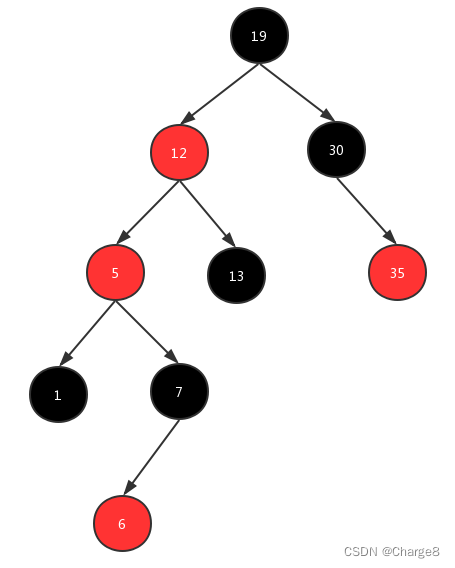
此时,当前指针:由 当前结点[12]变换为 父亲结点[5]。
3)右旋
右旋:当前父结点是红色,叔叔是黑色的时候,且当前的结点是左子树。右旋
- (1)把父结点变为黑色
- (2)把祖父结点(爷爷)变为红色
- (3)以祖父结点[19]作为右旋
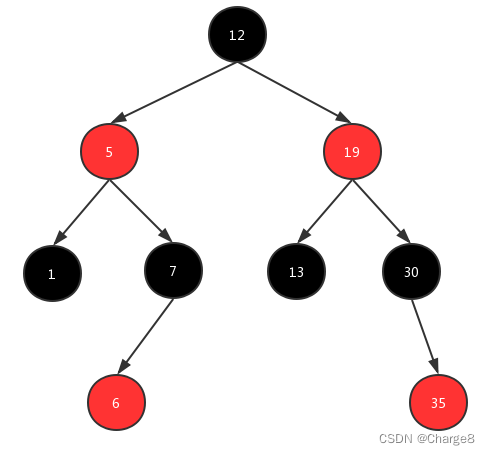
到此,插入结点[6] 完成。
5、结点删除
红黑树的删除是比较难的,需要按照二叉搜索树的删除原理,然后在变换颜色和旋转来满足红黑树的性质。
感兴趣的可以通过 演示动画自行了解。
红黑树演示动画:https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
6、性能分析
红黑树也是属于二叉搜索树的,所以:
- 插入:近似O(nlogn )
- 查找:O(logn)
- 删除:近似O(logn)
所以,红黑树的效率还是蛮快的,在内存中使用较多,比如 HashMap,Linux虚拟内存中的应用等。
更过红黑树自行了解或者查看参考文章,个人角色博主讲的很全,很详细。
参考文章:
- 史上最好理解的红黑树讲解,让你彻底搞懂红黑树:https://blog.csdn.net/cy973071263/article/details/122543826
– 求知若饥,虚心若愚。