---

一、什么是noise？

 
我们之前的讨论都是一种理想化的说明，比如数据来源于目标函数$f$，似乎我们手里拿到的数据是这样得来的，随机取一个输入，放入f中，获得一个输出，这样一个（输入，输出）pair就组成了一个样本。
 
但是实际过程不可能是这样的，误差存在于方方面面，

1. 首先对于输入，可能存在测量误差，比如我们手里拿到的一个数值10.5，有可能这个真实的数值是10。
2. 其次对于输出，也存在和输入一样的情况（对于连续值），当然对于分类任务，输出可能是错误的类别， 这也是noise。

 
在有噪音的情况下，机器学习流程如下：
 

 
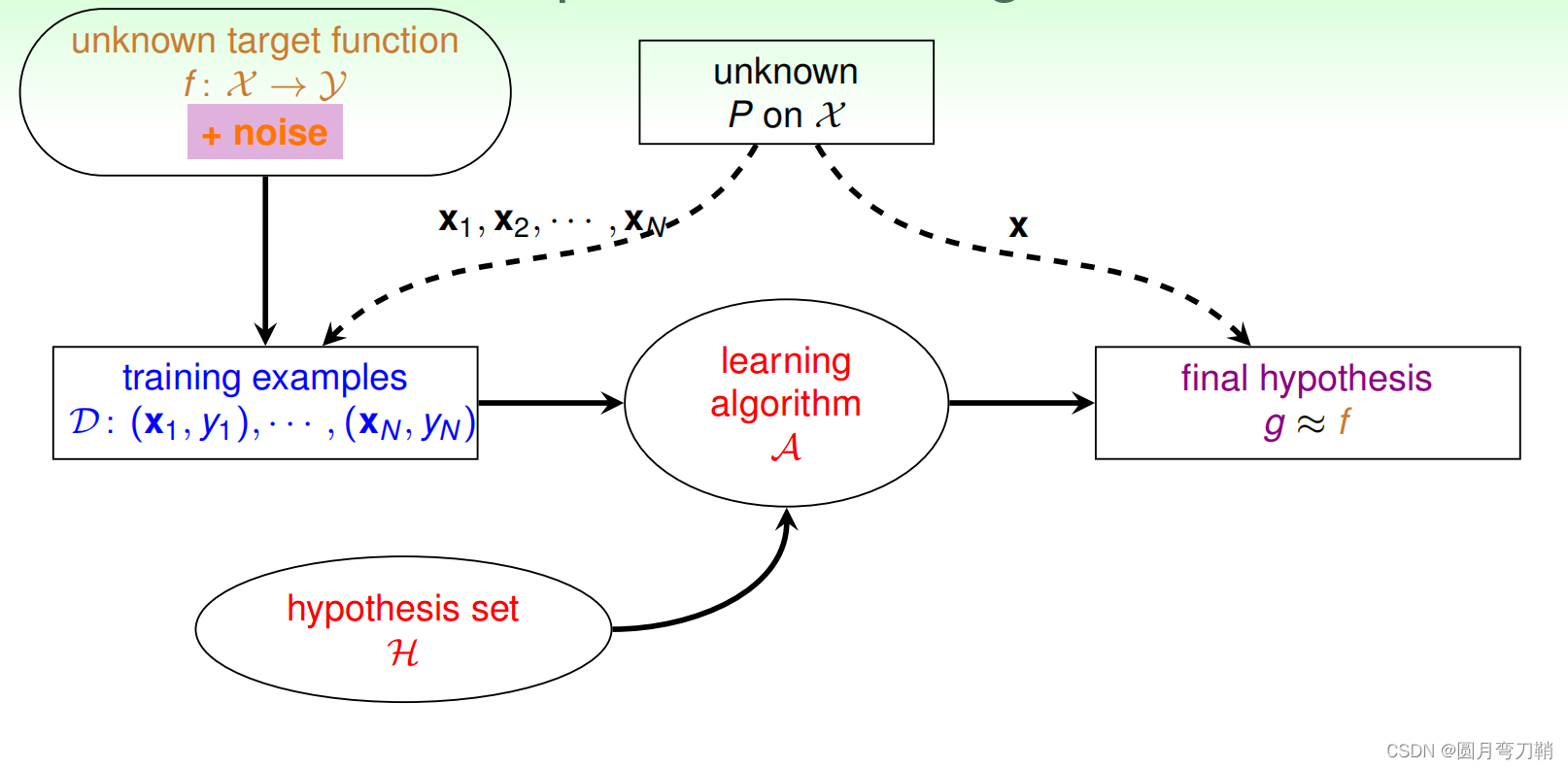
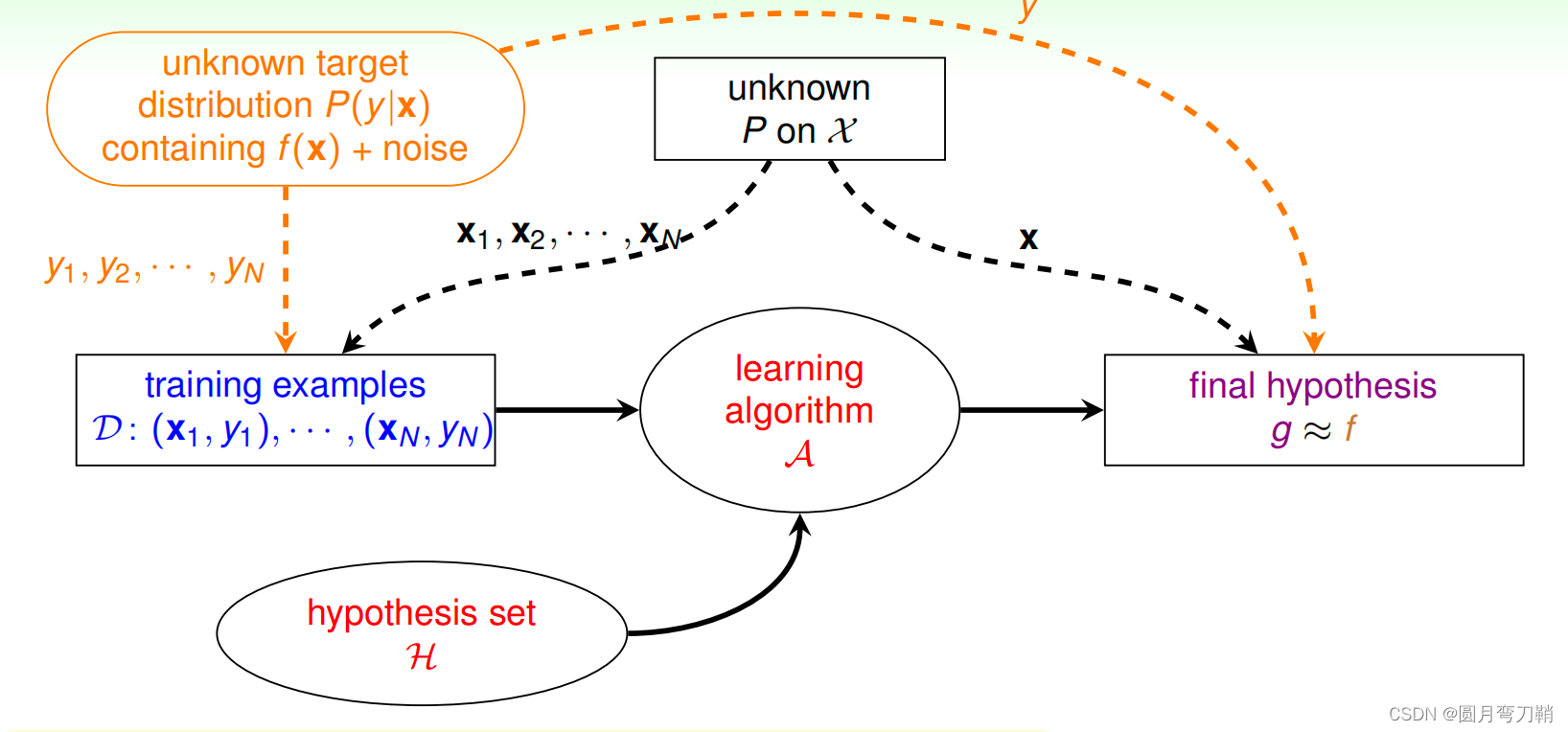
现在换一种说法，在理想情况下，给定某个输入$x$，输出是确定的$y=f(x)$，但是加上noise，输出就不是一个确定的值，而是一个分布$p(y|x)$，机器学习流程图可以表述成如下形式：
 

 
可喜可贺的是，PAC机器学习框架和上一篇内容介绍的vc理论在有noise的情况下也是成立的，也就是说，即使有噪声，机器学习仍然是可行的。

二、什么是error？

 
和noise不同，noise是无法避免的，但是error是我们自定义用来衡量机器学习结果和期望结果之间的差别的。针对不同的任务，不同的算法设计，error也不同：

1. 对于分类问题，常见的error就是误分类点的个数；
2. 当然，我们最常用的error还是用距离来度量的error，这种error在分类问题和回归问题上都可以用得到。常见的距离度量见此文章距离的度量。
    

error的设计不仅要考虑针对具体任务的合理性，也要考虑该error是否对于算法是易于优化的，通常我们希望error是可导的，所以距离度量型的error更常用。
 

三、常用error

 

1. 0/1损失
   $$error=count（\hat{y}\ne y）$$
    
2. 均方差损失MSE，$N$个样本误差
   $$error=\frac{1}{N}\sum _{i=0}^{N-1}(\widehat{y_i}-y_i{)}^2$$

 
3. 交叉熵损失cross entropy，针对$k$分类问题，单个样本误差
$$error=-\sum _{i=1}^k{y}_{i}log(p_i)$$
其中$p_i$表示模型将样本预测为类别$i$的概率，如果样本真实类别为$i$，则$y_i=1$，否则$y_i=0$。
所有样本的误差是取平均。