线性表

线性结构定义

常见线性结构

线性表

顺序表及其实现

顺序结构

顺序表的存储映像图

顺序表seqList及操作的定义（seqList.h）

顺序表基本操作的实现分析

查找操作

实现代码

插入操作

实现代码

删除操作

实现代码

顺序表应用——基本操作的测试

线性表

线性结构定义

Ø一组特征相同且数量有限的元素构成的集合。

Ø该集合可以为空，也可以不为空。

Ø当不为空时，有唯一一个元素被称为首元素，有唯一一个元素被称为尾元素。

Ø除了尾元素，每个元素有且仅有一个直接后继元素；除了首元素，每个元素有且仅有一个直接前驱元素。

常见线性结构

线性表(List)、时间有序表(Chronological Ordered List)、排序表(Sorted List)、频率有序表(Frequency Ordered List)等。

线性表：通过元素之间的相对位置来确定它们之间相互关系。

时间有序表：按元素到达结构的时间先后，确定元素之间的关系。栈/队列

排序表：据元素的关键字值来确定其间的关系。

频率有序表：按元素的使用频率确定它们之间的相互关系。

线性表

一种仅由元素的相互位置确定它们之间相互关系的线性结构，元素之间呈现出你先我后的关系。

线性表的规模或长度是指线性表中元素的个数。

特别地：当元素的个数为零时，该线性表称为空表。

线性表List的ADT ：描述关系和关系操作

Data: { xi | xi ∈ElemSet, i=1,2,3,……n, n > 0} 或 Φ; ElemSet为元素集合。

Relation: {<xi,xi+1>|xi,xi+1∈ElemSet, i=1,2,3,……n-1},

x1为首元素，xn为尾元素。

Operations:

initialize 前提: 无或指定List 的规模。结果: 分配相应空间及初始化。

isEmpty 前提：无结果：表List 为空返回true，否则返回false。

isFull 前提：无结果：表List 为满返回true，否则返回false。

length 前提：无结果：返回表List 中的元素个数。

get 前提：已知元素序号。

结果：如果该序号元素存在，则返回相应元素的数据值。

find 前提：已知元素的数据值。

结果：查找成功，返回元素的序号，否则返回查找失败标志。

insert 前提：已知待插入的元素及插入位置。

结果：如果插入位置合理，在指定位置插入该元素。

remove 前提：已知被删元素的值。

结果：首先按值查找相应元素，查找成功则删除该元素。

clear 前提: 无

结果：删除表List 中的所有元素。

常见的基本操作来源于生活中对这种结构的了解。

基本操作可以分为几大类型：结构类、属性类、数据操纵类、遍历类和典型应用类，

顺序表及其实现

顺序结构

Ø元素存放在内存中一块连续的空间里。

Ø借助存储空间物理上的连续性，元素可以按照其逻辑顺序依次存放，即元素存放的物理顺序和它的逻辑顺序是一致的。

Ø顺序存储的线性表称顺序表。

Ø在高级语言的固有数据类型中，数组在存储器中就表现为一块连续的空间，因此用数组实现顺序表非常合适。

Ø数组中各元素位置由其下标来表示，它同时也是相应元素的位置序号。

顺序表的存储映像图

elem为数组名字，数组存储线性表。

maxSize为len的上界；initSize为最大的存储空间数，maxSize=initSize-1

elem[0]用于其它特殊用途，如果不用于特殊用途maxSize=initSize

len 为元素个数，即顺序表长度；

顺序表seqList及操作的定义（seqList.h）

#include <iostream>
#define INITSIZE 100
using namespace std;
 
//用于异常处理中识别错误类别
class illegalSize{};
class outOfBound{};

template <class elemType>
class seqList
{    private:
        elemType *elem; // 顺序表存储数组，存放实际的数据元素。
        int len;        // 顺序表中的元素个数，亦称表的长度。
        int maxSize;    // 顺序表的的最大可能的长度。
        void doubleSpace(); //私有函数，做内部工具
 public:
        seqList(int size=INITSIZE); //初始化顺序表
        //表为空返回true,否则返回false。                    注意各处：
                                                   //       const和const &的用法
        bool isEmpty()const { return ( len == 0 ); }
        //表为满返回true，否则返回false。
        bool isFull()const { return (len == maxSize); }
        int length()const {return len;}  //表的长度，即实际存储元素的个数。
        
        elemType get(int i )const;//返回第i个元素的值
        //返回值等于e的元素的序号，无则返回0.
        int find (const elemType &e )const;
        //在第i个位置上插入新的元素（值为e），
        //使原来的第i个元素成为第i+1个元素。
        void insert(int i, const elemType &e );
        // 若第i个元素存在，删除并将其值放入e指向的空间。
        void remove(int i, elemType &e );
 
        void clear() { len=0; }; //清除顺序表，使得其成为空表
        ~seqList() { delete []elem; }; //释放表占用的动态数组
};
//属性赋初值，注意模板函数用法：帽子和胡须
template <class elemType>  seqList<elemType>::seqList(int size)
//初始化顺序表
{
    elem = new elemType[size];//申请动态数组
    if (!elem) throw illegalSize();
    maxSize = size-1; //0下标位置用于查找时做哨兵位。
    len = 0;
}
template <class elemType>
void seqList<elemType>::doubleSpace()
{   int i;
    elemType *tmp = new elemType[2*maxSize];
    if (!tmp) throw illegalSize();
 
    for (i=1; i<=len; i++)    tmp[i] = elem[i];
 
    delete []elem;   elem = tmp;
    maxSize = 2*maxSize - 1;
}

顺序表基本操作的实现分析

查找操作

待查元素放哨兵位，从后往前比较

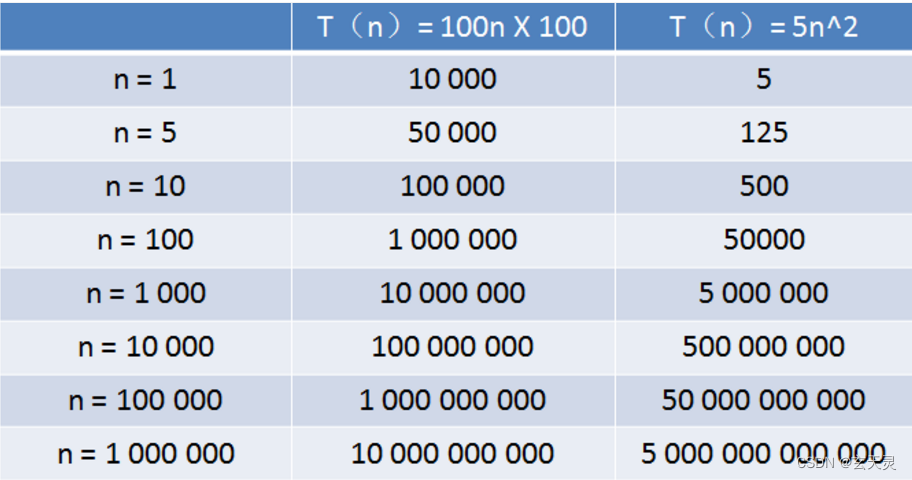
分析时间效率：

查找成功情况：

查找每个位置元素等概率1/n

平均： (1+2+…+n)1/n=（n+1)/2

时间复杂度：O(n)

查找不成功情况：

每次查找从尾部到哨兵位，比较n+1次

时间复杂度：O(n)

实现代码

template <class elemType> //注意各处const, const+&组合的用法
int seqList<elemType>::find (const elemType &e )const  
// 返回值等于e的元素的序号，无则返回0.
{
    int i;
    elem[0] = e;  //哨兵位先置为待查元素
    for (i=len; i>=0; i--)
        if (elem[i]==e) break;
    return i;
}

插入操作

新元素欲插在下标为i的位置，i可能的取值为n+1, n, … , 2, 1。

特别注意：

是从后往前至i位置逐个元素后移一位。

分析时间效率：

插入每个位置等概率1/（n+1）

移动的次数分别为0,1,2,…,n

平均： (1+2+…+n)/(n+1)=n/2

时间复杂度：O(n)

如何写出一个完成的程序？

“五步口诀法”：

1.参数检查

2.空间是否支持

3.核心操作

4.对其他属性的影响

5.正确返回

实现代码

template <class elemType>
void seqList<elemType>::insert (int i, const elemType &e )
{  int k;
    if ((i<1)||(i>len+1)) return; //插入位置越界
    if (len==maxSize) doubleSpace(); //空间满了，无法插入元素
    for (k=len+1; k>i; k--)        //循环注意：左右边界的检查
        elem[k]=elem[k-1];
    elem[i]=e;
    len++;
}

删除操作

待删元素在下标为i的位置，i可能的取值为n, … , 2, 1。

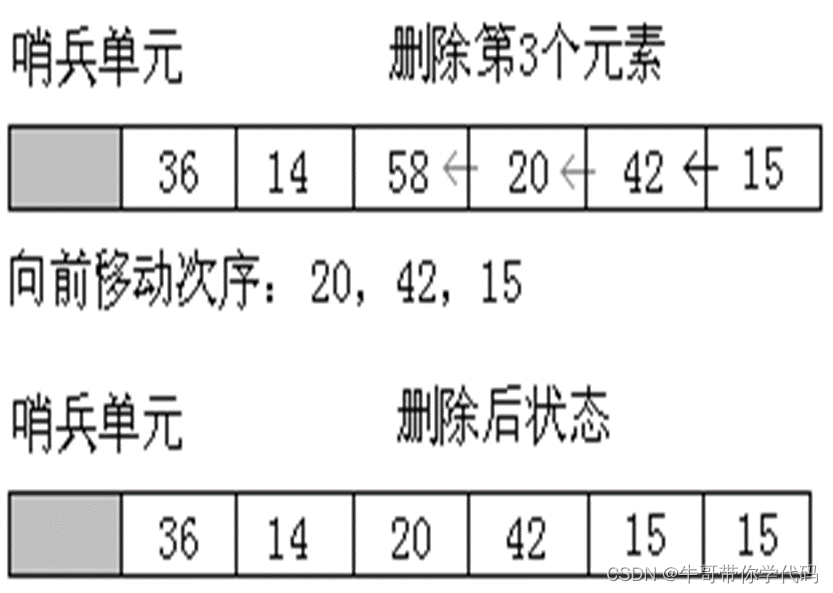
特别注意：

是自i+1位置开始，从前往后逐个元素前移一位。

分析时间效率：

删除每个位置等概率1/n

移动的次数分别为0,1,2,…,n-1

平均： (1+2+…+n-1)/n=（n-1）/2

时间复杂度：O(n)

实现代码

template <class elemType> //注意五步口诀法
void seqList<elemType>::remove (int i, elemType &e )
{  int k;
    if ((i<1)||(i>len)) return;
    e=elem[i];
    for (k=i; k<len; k++)
        elem[k]=elem[k+1];
    len--;
} 
template <class elemType> 
elemType seqList<elemType>::get(int i)const// 返回第i个元素的值
{
    if ((i<1)||(i>len)) throw outOfBound();
    return elem[i];
}

常见错误：

1.混淆len和maxSize的含义，前者是实际元素的个数，后者是存储空间的大小，也是最多能存多少元素的限制。

2.seqList对象作为函数形参，直接用对象形式而不用引用形式, 这样即浪费空间又引起seqList类的复制构造函数的执行，降低运行效率。

3.insert函数实现中忘记检查位置i的合理性、忘了检查表中是否有空间可以支持插入一个新的元素等，造成算法不完整。可以试着使用分析参数、空间检查、核心操作、对其他属性的影响、正确返回的“五步口诀法”，就可以设计出一个相对完整的程序。

顺序表应用——基本操作的测试

调用前面构造的seqlist.h

#include <iostream>
#include "seqlist.h"
using namespace std;
 
//求两个正整数集合的交集，用线性表处理集合问题。
int main()
{
    seqList<int> list1(20), list2(20), list3(20); //实例化对象
    int i, j, x;
    int len1,len3;
    //输入第一个整数集合中的元素，输入零结束：
    i=1;
    cout<<"输入第一个正整数集合，以零为结束标志：";
    cin>>x;
 
    while (x!=0)
    {
        list1.insert(i,x);
        i++;
        cin>>x;
    }
    //输入第二个整数集合中的元素，输入零结束：
    i=1;
    cout<<"输入第一个正整数集合，以零为结束标志：";
    cin>>x;
 
    while (x!=0)
    {
        list2.insert(i,x);
        i++;
        cin>>x;
    }
   //求list1,list2的交集，结果存入list3
    len1 = list1.length();
    j=1;
    for (i=1; i<=len1; i++)
    {
        x=list1.get(i);
        if (list2.find(x)!=0)
        {   
            list3.insert(j,x);
            j++;
        }
    }
   //显示list3中的元素
    cout<<"两个集合的交集元素为：";
    len3 = list3.length();
    for (i=1; i<=len3; i++)
    {
        x=list3.get(i);
        cout<<x<<" ";
    }
    cout<<endl;
    return 0;
}