文章目录
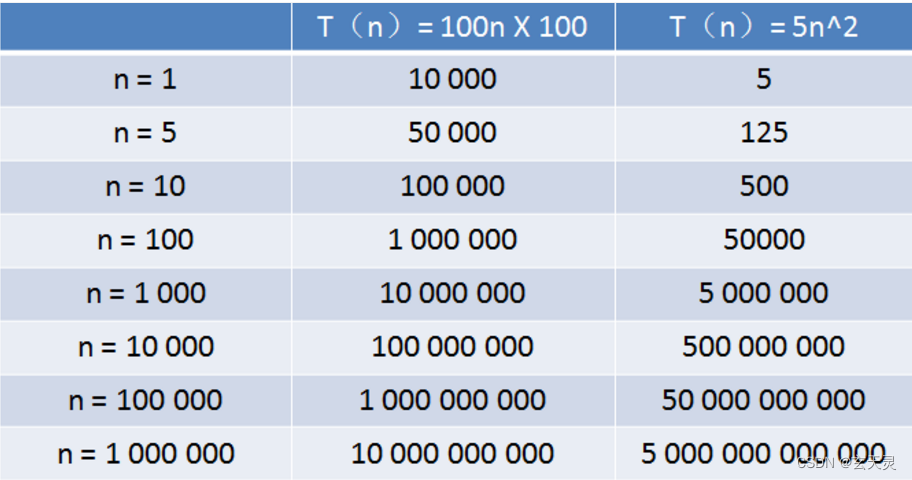
- 1. 优化目标
- 2. 大间距的直观理解
- 3. 大间距分类背后的数学
支持向量机(Support Vector Machines)是广泛应用于工业界和学术界的一种监督学习算法,在学习复杂的非线性方程时提供了一种更为清晰,更加强大的方式。下面从SVM的优化目标开始,通过对逻辑回归一点一点的修改来得到本质上的支持向量机。逻辑回归部分参考文章 机器学习——逻辑回归算法
1. 优化目标
在逻辑回归中我们已经熟悉了这里的假设函数形式,和右边的S型激励函数,用
z
z
z 表示
θ
T
x
\theta^Tx
θTx。

在逻辑回归中,如果有一个
y
=
1
y=1
y=1的样本,我们希望
h
θ
(
x
)
{{h}_{\theta }}\left( x \right)
hθ(x) 趋近1,因为我们想要正确地将此样本分类,这就意味着
θ
T
x
\theta^Tx
θTx 应当远大于0,这里的
>
>
>>
>>意思是远远大于0。这是因为由于
z
z
z 表示
θ
T
x
\theta^Tx
θTx,当
z
z
z远大于0时,即到了该图的右边,此时逻辑回归的输出将趋近于1。相反地,如果我们有另一个样本,即
y
=
0
y=0
y=0。我们希望假设函数的输出值将趋近于0,这对应于
θ
T
x
\theta^Tx
θTx,或者就是
z
z
z 会远小于0。
我们已经知道逻辑回归的代价函数表达式为:
C o s t ( h θ ( x ) , y ) = − y × l o g ( h θ ( x ) ) − ( 1 − y ) × l o g ( 1 − h θ ( x ) ) Cost\left( {h_\theta}\left( x \right),y \right)=-y\times log\left( {h_\theta}\left( x \right) \right)-(1-y)\times log\left( 1-{h_\theta}\left( x \right) \right) Cost(hθ(x),y)=−y×log(hθ(x))−(1−y)×log(1−hθ(x))
= − y × l o g ( 1 1 + e − θ T x ) − ( 1 − y ) × l o g ( 1 − 1 1 + e − θ T x ) =-y\times log\left(\frac{1}{1+{{e}^{-\theta^Tx}}}\right)-(1-y)\times log\left(1-\frac{1}{1+{{e}^{-\theta^Tx}}}\right) =−y×log(1+e−θTx1)−(1−y)×log(1−1+e−θTx1)
这里的 c o s t cost cost函数是一个训练样本所对应的表达式。现在我们考虑两种情况:一种是 y y y等于1的情况;另一种是 y y y 等于0的情况。
在第一种情况中,假设 y = 1 y=1 y=1 ,此时在目标函数中只需有第一项起作用,因为 y = 1 y=1 y=1时, ( 1 − y ) (1-y) (1−y)项将等于0。因此,当在 y = 1 y=1 y=1 的样本中时,即在 ( x , y ) (x, y) (x,y)中 ,我们得到 c o s t = − log ( 1 1 + e − z ) cost=-\log(\frac{1}{1+e^{-z}}) cost=−log(1+e−z1)这样一项。
用
z
z
z 表示
θ
T
x
\theta^Tx
θTx,即:
z
=
θ
T
x
z= \theta^Tx
z=θTx。如果画出关于
z
z
z 的函数,会看到左下角的这条曲线,我们可以看到,当
z
z
z 增大时,也就是相当于
θ
T
x
\theta^Tx
θTx增大时,
z
z
z 对应的值会变的非常小。这也就解释了,为什么逻辑回归在观察到正样本
y
=
1
y=1
y=1时,试图将
θ
T
x
\theta^Tx
θTx设置得非常大。因为,在代价函数中的这一项会变的非常小。
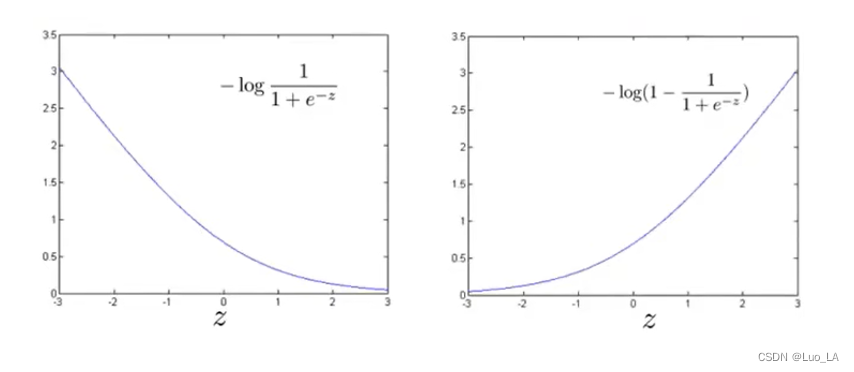
第二种情况,如果
y
=
0
y=0
y=0,此时在目标函数中只需有第二项起作用。因此,当在
y
=
0
y=0
y=0 的样本中时,我们得到
c
o
s
t
=
−
log
(
1
−
1
1
+
e
−
z
)
cost=-\log(1-\frac{1}{1+e^{-z}})
cost=−log(1−1+e−z1),得到右上的图像。
现在开始建立支持向量机,我们会从得到的代价函数开始,对
c
o
s
t
=
−
log
(
1
1
+
e
−
z
)
cost=-\log(\frac{1}{1+e^{-z}})
cost=−log(1+e−z1)做一点修改,取
z
=
1
z=1
z=1 点,画出将要用的新的代价函数,左下图。新的代价函数将是同逻辑回归非常相似的直线,也就是用紫红色画的线,由两条线段组成,即位于右边的水平部分和位于左边的直线部分。在SVM中我们将使用这个新的代价函数,我们把这个函数命名为
cos
t
1
(
z
)
{\cos}t_1{(z)}
cost1(z),对应着
y
=
1
y=1
y=1的情况。

另外一种情况是当 y = 0 y=0 y=0时,我们用同样的方法产生新的代价函数,如右上图,我们命名为 cos t 0 ( z ) {\cos}t_0{(z)} cost0(z)
拥有了上面两个新的代价函数定义之后,下面开始构造支持向量机。
对于逻辑回归的代价函数:
J
(
θ
)
=
1
m
∑
i
=
1
m
[
y
(
i
)
log
(
−
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
(
(
−
log
(
1
−
h
θ
(
x
(
i
)
)
)
)
]
+
λ
2
m
∑
j
=
1
n
θ
j
2
J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[{{y}^{(i)}}\log \left( -{h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)((-\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right))]}+\frac{\lambda }{2m}\sum\limits_{j=1}^{n}{\theta _{j}^{2}}
J(θ)=m1i=1∑m[y(i)log(−hθ(x(i)))+(1−y(i))((−log(1−hθ(x(i))))]+2mλj=1∑nθj2
对于支持向量机而言,实质上我们要将中括号内的前一项
l
o
g
(
h
θ
(
x
(
i
)
)
)
log\left( {h_\theta}\left( x^{(i)} \right) \right)
log(hθ(x(i)))替换为
cos
t
1
(
z
)
{\cos}t_1{(z)}
cost1(z),也就是
cos
t
1
(
θ
T
x
)
{\cos}t_1{(\theta^Tx)}
cost1(θTx),同样地,将后一项
−
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
-log\left(1- {h_\theta}\left( x^{(i)} \right) \right)
−log(1−hθ(x(i)))替换为
cos
t
0
(
z
)
{\cos}t_0{(z)}
cost0(z),也就是
cos
t
0
(
θ
T
x
)
{\cos}t_0{(\theta^Tx)}
cost0(θTx)。这里的代价函数
cos
t
1
{\cos}t_1
cost1,
cos
t
0
{\cos}t_0
cost0,就是之前所提到的那两条线。因此,对于支持向量机,我们得到了这里的最小化问题,即:

现在,按照支持向量机的惯例,事实上,我们的书写会稍微有些不同,代价函数的参数表示也会稍微有些不同。
首先,我们要除去 1 / m 1/m 1/m这一项,因为 1 / m 1/m 1/m 仅是个常量,因此在这个最小化问题中,无论前面是否有 1 / m 1/m 1/m 这一项,最终我所得到的最优值 θ {{\theta }} θ都是一样的。
第二点概念上的变化,是在正则化方面的变化。对于逻辑回归,在目标函数中,我们有两项:第一个是训练样本的代价,第二个是我们的正则化项,通过正则参数 λ \lambda λ来权衡这两项。但对于支持向量机,按照惯例,我们将使用一个不同的参数替换这里的 λ \lambda λ,这个参数称为 C C C。可以把这里的参数 C C C 考虑成 1 / λ 1/\lambda 1/λ。
因此,这就得到了在支持向量机中的整个优化目标函数。然后最小化这个目标函数,得到SVM 学习到的参数
θ
{{\theta}}
θ。
m
i
n
C
∑
i
=
1
m
[
y
(
i
)
cos
t
1
(
θ
T
x
(
i
)
)
+
(
1
−
y
(
i
)
)
cos
t
0
(
θ
T
x
(
i
)
)
]
+
1
2
∑
j
=
1
n
θ
j
2
min C\sum\limits_{i=1}^{m}{[{{y}^{(i)}}{\cos}t_1{(\theta^Tx^{(i)})}+\left( 1-{{y}^{(i)}} \right){\cos}t_0{(\theta^Tx^{(i)})}]}+\frac{1}{2}\sum\limits_{j=1}^{n}{\theta _{j}^{2}}
minCi=1∑m[y(i)cost1(θTx(i))+(1−y(i))cost0(θTx(i))]+21j=1∑nθj2
有别于逻辑回归输出的概率。在这里,当最小化代价函数,获得参数
θ
{{\theta }}
θ时,支持向量机所做的是它来直接预测
y
y
y的值等于1,还是等于0。
2. 大间距的直观理解
人们有时将支持向量机看作是大间距分类器。在这一部分,将介绍其中的含义,这有助于我们直观理解SVM模型的假设是什么样的。

最小化代价函数的必要条件是,如果你有一个正样本,
y
=
1
y=1
y=1,则只有在
z
>
=
1
z>=1
z>=1时,代价函数
cos
t
1
(
z
)
{\cos}t_1{(z)}
cost1(z)才等于0。换句话说,如果你有一个正样本,我们会希望
θ
T
x
>
=
1
\theta^Tx>=1
θTx>=1,反之,如果
y
=
0
y=0
y=0,函数
cos
t
0
(
z
)
{\cos}t_0{(z)}
cost0(z),它只有在
z
<
=
−
1
z<=-1
z<=−1的区间里函数值为0。
事实上,如果你有一个正样本 y = 1 y=1 y=1,则其实我们仅仅要求 θ T x \theta^Tx θTx大于等于0,就能将该样本恰当分出,这是因为如果 θ T x \theta^Tx θTx>0大的话,我们的模型代价函数值为0,但是,支持向量机的要求更高,不仅仅要能正确分开输入的样本,即不仅仅要求 θ T x \theta^Tx θTx>0,我们需要的是比0值大很多,比如大于等于1, y = 1 y=1 y=1的情况类似。这就相当于在支持向量机中嵌入了一个额外的安全因子,或者说安全的间距因子。
具体而言,接下来会考虑一个特例。我们将这个常数 C C C设置成一个非常大的值。比如100000或者其它非常大的数,然后来观察支持向量机会给出什么结果?
如果 C C C非常大,则最小化代价函数的时候,我们将会很希望找到一个使第一项为0的最优解。因此,让我们尝试在代价项的第一项为0的情形下理解该优化问题。这将给我们一些关于支持向量机模型的直观感受。
当输入一个训练样本标签为 y = 1 y=1 y=1,需要找到一个 θ {{\theta }} θ,使得 θ T x > = 1 \theta^Tx>=1 θTx>=1,类似地,标签为 y = 0 y=0 y=0,需要 θ T x < = − 1 \theta^Tx<=-1 θTx<=−1。这里第一项是 C C C乘以0,因此可以将其删去,得到代价函数表达式 m i n 1 2 ∑ j = 1 n θ j 2 min \frac{1}{2}\sum\limits_{j=1}^{n}{\theta _{j}^{2}} min21j=1∑nθj2。这样当求解这个优化问题,最小化这个关于变量 θ {{\theta }} θ的函数的时候,会得到一个非常有趣的决策边界。
给出下图一个数据集,其中有正样本,也有负样本,可以看到这个数据集是线性可分的。有多条不同的直线,可以把正样本和负样本完全分开。

支持向量机将会选择这个黑色的决策边界,相较于粉色或者绿色画的决策界,这条黑线看起来是更稳健的决策界。在分离正样本和负样本上它显得的更好。这条黑线有更大的距离,这个距离叫做间距(margin)。
黑色的决策界和训练样本之间有更大的最短距离。粉线和蓝线离训练样本就非常近,在分离样本的时候就会比黑线表现差。因此,这个距离叫做支持向量机的间距,而这是支持向量机具有鲁棒性的原因,因为它努力用一个最大间距来分离样本。因此支持向量机有时被称为大间距分类器。
3. 大间距分类背后的数学
这部分在吴恩达视频课程中作为选修,但是我听了之后感觉会对SVM的大间距分类器产生更好的理解。
首先,复习一下关于向量内积的知识。假设有两个向量,
u
u
u和
v
v
v,
u
=
[
u
1
,
u
2
]
u=[u_1,u_2]
u=[u1,u2],
v
=
[
v
1
,
v
2
]
v=[v_1,v_2]
v=[v1,v2]。
u
T
v
u^T v
uTv也叫做向量
u
u
u和
v
v
v之间的内积。由于是二维向量,可以将它们画在这个图上。
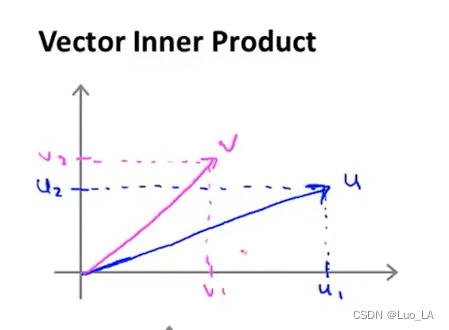
向量
u
u
u,在横轴上,取值为某个
u
1
{{u}_{1}}
u1,而在纵轴上,高度是某个
u
2
{{u}_{2}}
u2作为
u
u
u的第二个分量。很容易向量
u
u
u的范数,
∥
u
∥
\left\| u \right\|
∥u∥表示
u
u
u的范数,即
u
u
u的长度,即向量
u
u
u的欧几里得长度。根据毕达哥拉斯定理,
∥
u
∥
=
u
1
2
+
u
2
2
\left\| u \right\|=\sqrt{u_{1}^{2}+u_{2}^{2}}
∥u∥=u12+u22,这是向量
u
u
u的长度,是一个实数。
我们来看看如何计算
u
u
u和
v
v
v之间的内积。我们将向量
v
v
v投影到向量
u
u
u上,做一个直角投影,设这条红线的长度为
p
p
p,因此
p
p
p是
v
v
v投影到向量
u
u
u上的长度,因此可以得到
u
T
v
=
p
⋅
∥
u
∥
{{u}^{T}}v=p\centerdot \left\| u \right\|
uTv=p⋅∥u∥。

需要注意的就是
p
p
p值,
p
p
p事实上是有符号的,即它可能是正值,也可能是负值。在内积计算中,如果
u
u
u和
v
v
v之间的夹角小于90度,那么那条红线的长度
p
p
p是正值。然而如果这个夹角大于90度,则
p
p
p将会是负的。
内积的另一个计算公式是:
u
T
v
=
u
1
×
v
1
+
u
2
×
v
2
u^T v={{u}_{1}}\times {{v}_{1}}+{{u}_{2}}\times {{v}_{2}}
uTv=u1×v1+u2×v2。

上面的公式是先前给出的支持向量机模型中的目标函数。为了讲解方便,做一点简化,仅仅是为了让目标函数更容易被分析。
首先,忽略掉截距,令
θ
0
=
0
{{\theta }_{0}}=0
θ0=0,这样更容易画示意图。
然后,将特征数
n
n
n置为2,因此我们仅有两个特征
x
1
,
x
2
{{x}_{1}},{{x}_{2}}
x1,x2,目标函数可以写作:
1
2
(
θ
1
2
+
θ
2
2
)
=
1
2
(
θ
1
2
+
θ
2
2
)
2
\frac{1}{2}\left({\theta_1^2+\theta_2^2}\right)=\frac{1}{2}\left(\sqrt{\theta_1^2+\theta_2^2}\right)^2
21(θ12+θ22)=21(θ12+θ22)2,只有两个参数
θ
1
,
θ
2
{{\theta }_{1}},{{\theta }_{2}}
θ1,θ2。因为忽略了
θ
0
{{\theta }_{0}}
θ0,注意到括号里面的这一项是向量
θ
{{\theta }}
θ的范数,或者说是向量
θ
{{\theta }}
θ的长度,得到我们的目标函数是等于
1
2
∥
θ
∥
2
\frac{1}{2}\left\| \theta \right\|^2
21∥θ∥2。因此支持向量机做的全部事情,就是极小化参数向量
θ
{{\theta }}
θ范数的平方,或者说长度的平方。
我们考察一个单一的训练样本,在下图中用一个叉来表示这个样本
x
(
i
)
x^{(i)}
x(i),意思是在水平轴上取值为
x
1
(
i
)
x_1^{(i)}
x1(i),在竖直轴上取值为
x
2
(
i
)
x_2^{(i)}
x2(i)。现在,把一个参数向量也画成向量,那么内积
θ
T
x
(
i
)
θ^T x^{(i)}
θTx(i) 将会是什么呢?
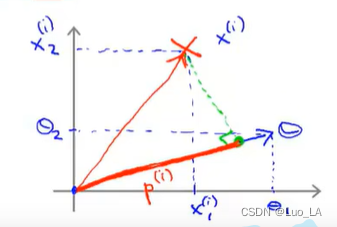
使用我们之前的方法,我们计算的方式就是将训练样本投影到参数向量
θ
{{\theta }}
θ,将它称为
p
(
i
)
p^{(i)}
p(i)用来表示这是第
i
i
i个训练样本在参数向量
θ
{{\theta }}
θ上的投影。根据之前的内容,我们知道的是
θ
T
x
(
i
)
θ^Tx^{(i)}
θTx(i)将会等于
p
p
p 乘以向量
θ
θ
θ 的长度或范数,即
θ
T
x
(
i
)
=
p
(
i
)
⋅
∥
θ
∥
θ^Tx^{(i)}=p^{(i)}\cdot{\left\| \theta \right\|}
θTx(i)=p(i)⋅∥θ∥ 。这就等于
θ
1
⋅
x
1
(
i
)
+
θ
2
⋅
x
2
(
i
)
\theta_1\cdot{x_1^{(i)}}+\theta_2\cdot{x_2^{(i)}}
θ1⋅x1(i)+θ2⋅x2(i)。这两种方式是等价的,都可以用来计算
θ
θ
θ和
x
(
i
)
x^{(i)}
x(i)之间的内积。
这里表达的意思是:这个 θ T x ( i ) > = 1 θ^Tx^{(i)}>=1 θTx(i)>=1 或者 θ T x ( i ) < − 1 θ^Tx^{(i)}<-1 θTx(i)<−1的约束,是可以被 p ( i ) ⋅ ∥ θ ∥ > = 1 p^{(i)}\cdot{\left\| \theta \right\|} >=1 p(i)⋅∥θ∥>=1这个约束所代替的。
现在让我们考虑下面这里的训练样本,我们使用上面得到的优化目标函数等于
1
2
∥
θ
∥
2
\frac{1}{2}\left\| \theta \right\|^2
21∥θ∥2。

现在,继续使用之前的简化,即
θ
0
=
0
{{\theta }_{0}}=0
θ0=0,我们来看一下支持向量机会选择什么样的决策界。如左下图中的绿色边界是一种选择,这不是一个非常好的选择,因为它的间距很小。这个决策界离训练样本的距离很近。支持向量机不会选择它作为边界。
对于绿色边界这种选择,其对应的的参数
θ
{{\theta }}
θ事实上是和决策界是90度正交的,因为作为边界,其分类的结果为正样本和负样本,所以就有边界上的
θ
T
x
(
i
)
=
0
θ^Tx^{(i)}=0
θTx(i)=0,因此两个向量是正交的。又因为
θ
0
=
0
{{\theta }_{0}}=0
θ0=0的简化意味着决策界必须通过原点
(
0
,
0
)
(0,0)
(0,0)。现在让我们看一下这对于优化目标函数意味着什么。

如上右图蓝色标记的样本点,假设第一个样本是
x
(
1
)
x^{(1)}
x(1),如果考察这个样本到参数
θ
{{\theta }}
θ的投影,投影是短的红线段,等于
p
(
1
)
p^{(1)}
p(1),它非常短。类似地,第二个样本点是
x
(
2
)
x^{(2)}
x(2),把它到
θ
{{\theta }}
θ的投影画成粉色,等于
p
(
2
)
p^{(2)}
p(2)这个投影也非常短。
p
(
2
)
p^{(2)}
p(2)事实上是一个负值,因为这个向量和参数向量
θ
{{\theta }}
θ的夹角大于90度。
我们会发现这些
p
(
i
)
p^{(i)}
p(i)将会是非常小的数,因此当我们考察优化目标函数的时候,对于正样本而言,我们需要
p
(
i
)
⋅
∥
θ
∥
>
=
1
p^{(i)}\cdot{\left\| \theta \right\|}>=1
p(i)⋅∥θ∥>=1,但是如果
p
(
i
)
p^{(i)}
p(i)在这里非常小,那就意味着我们需要
θ
{{\theta }}
θ的范数非常大。类似地,对于负样本而言我们需要
p
(
2
)
⋅
∥
θ
∥
<
=
−
1
p^{(2)}\cdot{\left\|\theta \right\|}<=-1
p(2)⋅∥θ∥<=−1,我们已经在上面的样本中得到
p
(
2
)
p^{(2)}
p(2)会是一个非常小的数,因此唯一的办法就是
θ
{{\theta }}
θ的范数变大。但是我们的目标函数是希望找到一个参数
θ
{{\theta }}
θ,它的范数是小的。因此,这看起来不像是一个好的参数向量
θ
{{\theta }}
θ的选择。
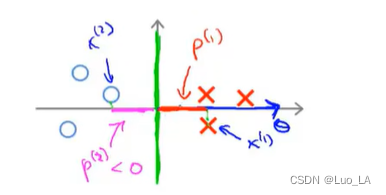
相反的,来看一个不同的决策边界。如上图所示的绿色边界,这个绿色的决策界有一个垂直于它的向量
θ
{{\theta }}
θ。现在如果考察样本
x
(
1
)
x^{(1)}
x(1),将它投影到
θ
{{\theta }}
θ上,就会得到这样
p
(
1
)
p^{(1)}
p(1)。另一个样本
x
(
2
)
x^{(2)}
x(2)做同样的投影。注意到现在
p
(
1
)
p^{(1)}
p(1) 和
p
(
2
)
p^{(2)}
p(2)这些投影长度是长多了。这时,当我们满足约束
P
(
i
)
⋅
∥
θ
∥
>
1
P^{(i)}\cdot{\left\| \theta \right\|}>1
P(i)⋅∥θ∥>1时,则因为
p
(
i
)
p^{(i)}
p(i)变大了,
θ
{{\theta }}
θ的范数就可以变小了。因此这意味着通过选择这种决策界,支持向量机可以使参数
θ
{{\theta }}
θ的范数变小很多。因此,如果我们想令
θ
{{\theta }}
θ的范数变小,从而令
θ
{{\theta }}
θ范数的平方变小,就能让支持向量机选择上面这种决策界。这就是支持向量机如何能有效地产生大间距分类的原因。
通过让间距变大,即通过增大这些 p ( 1 ) , p ( 2 ) , p ( 3 ) p^{(1)},p^{(2)},p^{(3)} p(1),p(2),p(3)等等的值,支持向量机最终可以找到一个较小的 θ {{\theta }} θ范数。这正是支持向量机中最小化目标函数的目的。
最后一点,我们的推导自始至终使用了这个简化假设,就是参数 θ 0 = 0 θ_0=0 θ0=0,作用是让决策界通过原点。但是可以说明的是,即便 θ 0 θ_0 θ0不等于0,支持向量机仍然会找到正样本和负样本之间的大间距分隔,在这里就不再做解释了。
以上就解释了为什么支持向量机是一个大间距分类器。





![DonkeyCar [02] - 软件配置 - 上位机(windows)](https://img-blog.csdnimg.cn/d4f2b13881f242dfb47d6b616075c574.png)