机器学习第6天：线性回归模型正则化

news2024/10/6 6:48:44

文章目录

机器学习专栏

正则化介绍

岭回归

岭回归成本函数

核心代码

示例

Lasso回归

Lasso回归损失函数

核心代码

弹性网络

弹性网络成本函数

核心代码

结语

机器学习专栏

机器学习_Nowl的博客-CSDN博客

正则化介绍

作用：正则化是为了防止模型过拟合

原理：在损失函数中加入一个正则项，使模型减少损失的同时还要降低模型复杂度

它往往给模型约束，来使它无法完全迎合训练集数据

在本文中我们将看到三种正则化方法

三种方法思想差不多，只是约束模型复杂度的方法不同

岭回归

岭回归成本函数

$J(w)=MSE(w)+a*\frac{1}{2}*\sum_{i=1}^{n}w^{2}$

我们先前已经知道MSE损失函数，这个公式后面加的项就叫作正则项，岭回归的正则项是l2范数的平方的一半

$a*\frac{1}{2}*\sum_{i=1}^{n}w^{2}$

此时模型训练时就不能只考虑MSE函数的损失了，还必须减小w参数的大小（降低模型复杂度，减少过拟合的可能性）

核心代码

以下是sklearn库使用岭回归的基本代码

from sklearn.preprocessing import PolynomialFeatures


model = Ridge(alpha=1)
model.fit(x, y)

alpha就是公式中的a参数，越小则代表正则程度越小

我们来看几种不同alpha的情况

该图参数从左到右逐渐增大（岭回归越强），可以看到模型的复杂度也逐渐降低了

示例

我们已经清楚一点，正则化能让模型变得更简单，考虑以下情景

我们有这样一组数据

可以看到，开始的点排列的还是很有规律的，但是右上角的点显得非常突兀，那么如果进行普通的预测

可能得到以下结果

而使用岭回归可能得到更好的结果，如下

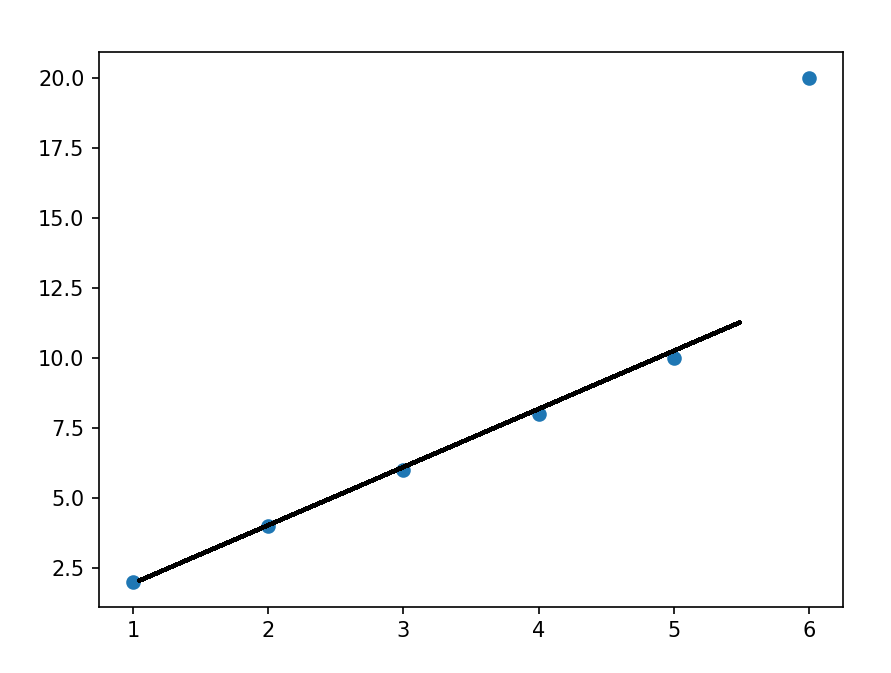
再一次体现了正则化的作用（防止模型过拟合而降低泛化能力）

我们也可以看一个代码示例

分别用线性模型和加入正则的模型拟合数据

from sklearn.linear_model import Ridge
from sklearn.linear_model import LinearRegression
import numpy as np

x = np.random.rand(100, 1)
y = 4 * x + np.random.rand(100, 1)


model1 = LinearRegression()
model1.fit(x, y)
print(model1.coef_)

model = Ridge(alpha=1)
model.fit(x, y)
print(model.coef_)

看看它们拟合的参数

可以看到岭回归拟合的模型更简单（在这个实例中当然效果不好，这里只是为了演示它的作用，在实际情况中我们应该用指标测试模型是否过拟合了，再尝试使用岭回归）

Lasso回归

Lasso回归损失函数

Lasso回归公式和岭回归类似，只不过它的正则项是l1范数，它与岭回归的一个区别是它倾向于完全消除掉最不重要的特征

$J(w)=MSE(w)+a*\sum_{i=1}^{n}\left | w \right |$

则正则项为

$a*\sum_{i=1}^{n}\left | w \right |$

效果与岭回归相同

核心代码

以下是sklearn库使用Lasso回归的基本代码

from sklearn.linear_model import Lasso

model = Lasso(alpha=1)
model.fit(x, y)

alpha就是公式中的a参数，越小则代表正则程度越小

弹性网络

弹性网络成本函数

弹性网络是岭回归于Lasso回归的中间地带，你可以控制r来控制其他两种正则化方法的混合程度，r为0时，弹性网络就是岭回归，为1时，弹性网络就是Lasso回归

$J(w)=MSE(w)+ra\sum_{i=1}^{n}\left | w \right |+\frac{1-r}{2}a\sum_{i=1}^{n}w^{2}$

正则项为

$ra\sum_{i=1}^{n}\left | w \right |+\frac{1-r}{2}a\sum_{i=1}^{n}w^{2}$

核心代码

以下是sklearn库使用弹性网络的基本代码

from sklearn.linear_model import ElasticNet

model = ElasticNet(alpha=0.1, l1_radio=0.5)
model.fit(x, y)

alpha对应公式中的a参数，l1_radio对应公式中的r

结语

在具体任务中，我们应该用学习曲线或其他性能判断模型是否过拟合后再考虑使用正则化，同时根据不同特征选取不同的正则化方法

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1222621.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！