【用unity实现100个游戏之15】开发一个类保卫萝卜的Unity2D塔防游戏5(附项目源码,完结)
news2026/2/15 3:00:44
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1222612.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
ExoPlayer架构详解与源码分析(9)——TsExtractor
系列文章目录
ExoPlayer架构详解与源码分析(1)——前言 ExoPlayer架构详解与源码分析(2)——Player ExoPlayer架构详解与源码分析(3)——Timeline ExoPlayer架构详解与源码分析(4)—…
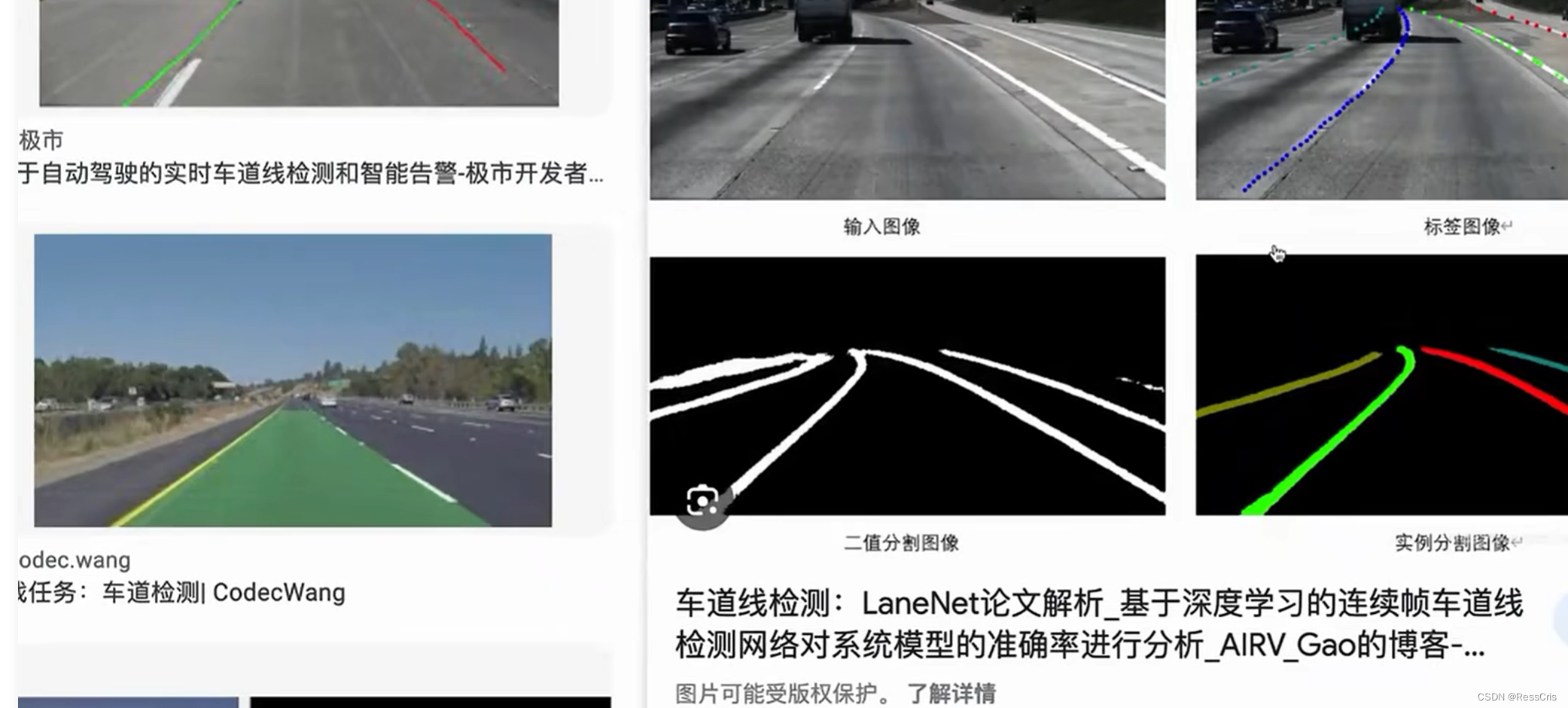
智能驾驶汽车虚拟仿真视频数据理解(一)
赛题官网
datawhale 赛题介绍 跑通demo paddle 跑通demo torch
提交的障碍物取最主要的那个?不考虑多物体提交。障碍物,尽可能选择状态发生变化的物体。如果没有明显变化的,则考虑周边的物体。车的状态最后趋于减速、停止,时序…
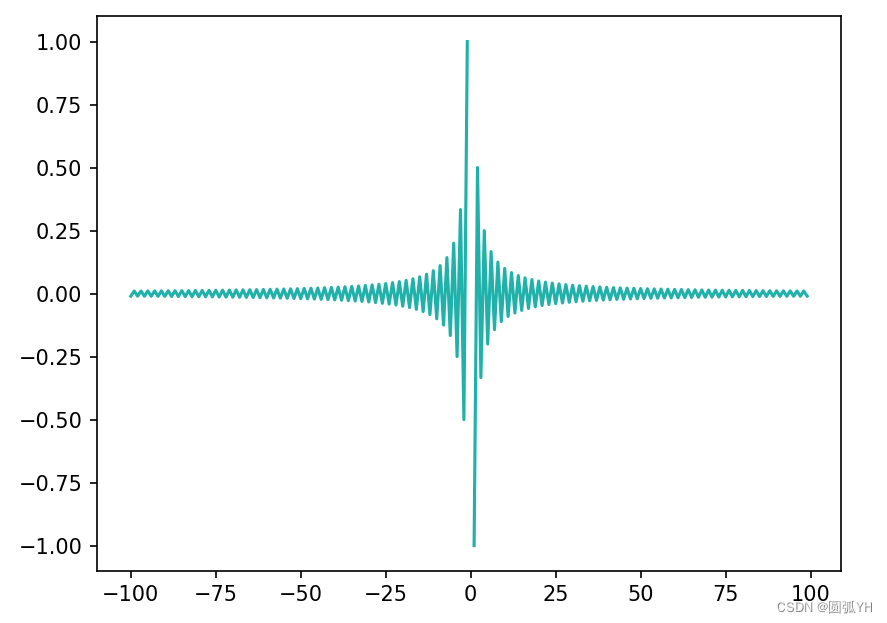
python→函数曲线
CSDN中公式一栏,亦可以插入Latex函数。
以函数 为例
也可以用Latex写如下代码:
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[
y
\frac{n}{n30}
\]
\end{document}
如下: 那么,该函数图像如何呢…
vue+element实现多级表头加树结构
标题两种展示方式
方式一 完整代码:
<template><div class"box"><el-tableref"areaPointTable":data"tableData"border:span-method"objectSpanMethod":header-cell-style"tableHeaderMerge"><el-ta…
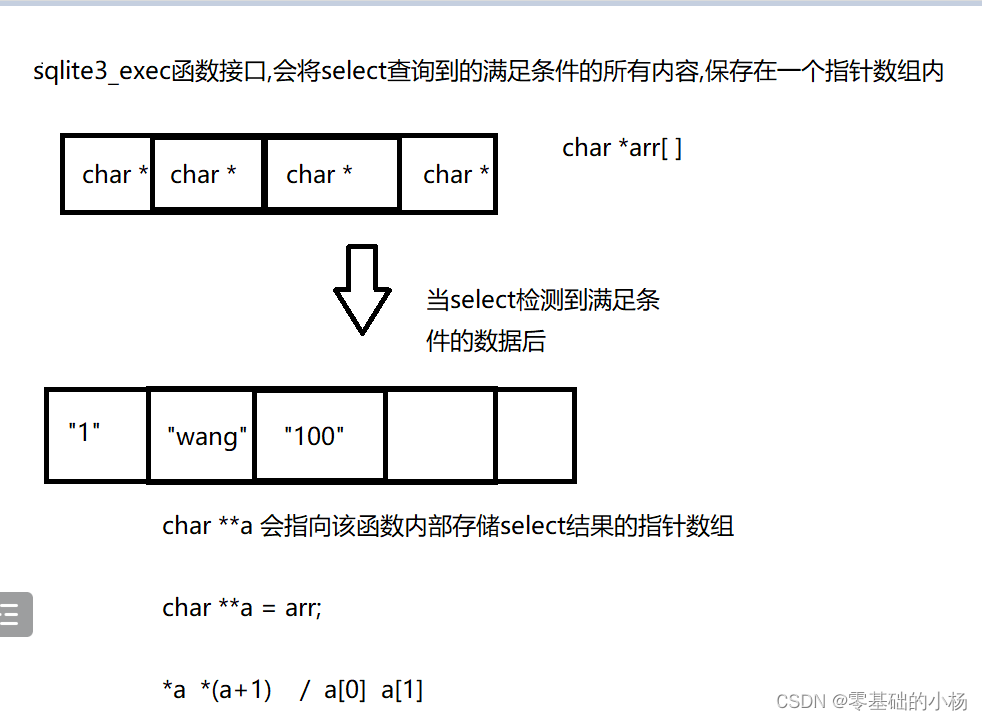
数据库编程sqlite3库安装及使用
数据库编程 数据库的概念 数据库是“按照数据结构来组织、存储和管理数据的仓库”。是一个长期存储在计算机内的、有组织的、可共享的、统一管理的大量数据的集合。 数据库是存放数据的仓库。它的存储空间很大,可以存放百万条、千万条、上亿条数据。但是数据库并不是…
一起学docker系列之五docker的常用命令--操作容器的命令
目录 前言1 启动容器2 查看容器3 退出容器4 启动已经停止的容器5 重启容器6 停止容器7 删除已经停止的容器8 启动容器说明和举例9 查看容器日志10 查看容器内运行的进程11 查看容器内部细节12 进入正在运行的容器并进行交互13 导入和导出容器结语 前言
当涉及到容器化技术&…
Java学习之路 —— 网络通信
文章目录 1. InetAddress2. UDP3. TCP4. 总结 1. InetAddress
InetAddress的常用方法如下:
public class InetAddressDemo {public static void main(String[] args) throws Exception{// 1. 获取本机IP地址对象InetAddress ip1 InetAddress.getLocalHost();Sys…
飞熊领鲜参加「第十届中国产业数字化大会」获创新企业数字化百强
11月16日至17日,托比网“第十届中国(南京)产业数字化大会”在南京举行。作为“中国(南京)电子商务大会”的一部分,本次会议由江苏省商务厅、南京市人民政府指导,南京市商务局、南京市鼓楼区人民…
Windows安装Java环境(OracleJDK)
在下载之前,我们先了解一下java的前世今生
1991年:Java 的前身 Oak 由 James Gosling 和他的团队在 Sun Microsystems 公司开发。1995年:Oak 更名为 Java,并在同年发布。Java 1.0 版本正式推出。1996年:Sun Microsyst…
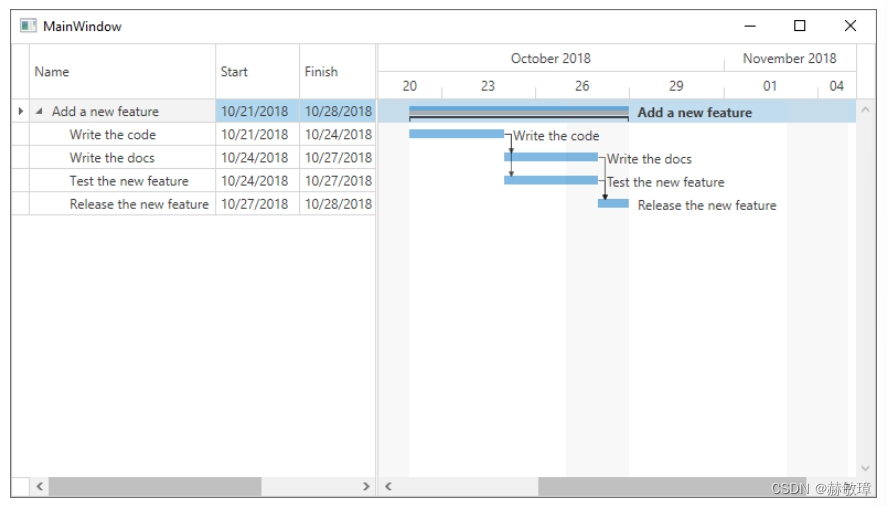
wpf devexpress 添加GanttControl到项目
这个教程示范如何添加GanttControl 到你的项目使用内置GanttControl数据类。
要求
添加 Devexpress.Wpf.Gantt Nuget包到你的项目使用GanttControl. 数据模型
GanttControl携带和内置数据对象,可以使用创建视图模型:
GanttTask
呈现甘特图任务
Gan…
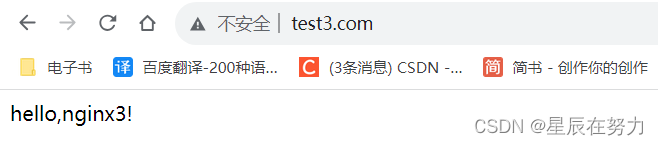
web服务器练习---配置nginx三种虚拟主机
在做实验之前,大家先安装nginx服务,有两种安装方法:
1、rpm包安装(安装过程简单,适用于学习阶段,方便测试)
2、源码安装(安装过程较为复杂,适用于生产环境)…
每天一点python——day69
#字符串的比较操作使用的符号:
>[大于],>[大于等于],<[小于],<[小于等于],[等于],![不等于]#如图: #例子:比较原理释义:每个字符在计算机里面都有一个原始值…
如何解決開機後出現BitLocker修復畫面/取得BitLocker金鑰
[Notebook/Desktop/AIO] 疑難排解 - 如何解決開機後出現BitLocker修復畫面/取得BitLocker金鑰
如果您遇到開機進入系統後出現BitLocker修復畫面,這表示您電腦的硬碟已受BitLocker保護(硬碟被鎖住)。當系統在維修以及其他因素下做過硬體變動或BIOS更新設置變動&…
【大模型应用开发教程】动手学大模型应用开发,一起探索LLM Universe
动手学大模型应用开发 01 开源初心02 教程内容03 学习指南04 文章最后 原文链接-奇想星球
LLM 正逐步成为信息世界的新革命力量,其通过强大的自然语言理解、自然语言生成能力,为开发者提供了新的、更强大的应用开发选择。随着国内外井喷式的 LLM API 服…
【云服务器选型指南:五大关键】
云服务器选型指南
写在前面
在云计算时代,云服务器(Elastic Compute Service, ECS)凭借其简单高效、安全可靠、处理能力可弹性伸缩等特点,成为构建稳定、安全应用的首选。相比物理服务器,云服务器的管理方式更为简单…
盘点52个Python各行各业管理系统源码Python爱好者不容错过
盘点52个Python各行各业管理系统源码Python爱好者不容错过
学习知识费力气,收集整理更不易。
知识付费甚欢喜,为咱码农谋福利。
源码下载链接:https://pan.baidu.com/s/1pcP-94UY_57sAd2oDB3i6Q?pwd8888
提取码:8888
项目名…
Flume学习笔记(1)—— Flume入门
Flume 概述
Flume 是 Cloudera 提供的一个高可用的,高可靠的,分布式的海量日志采集、聚合和传输的系统
Flume 基于流式架构,灵活简单
Flume最主要的作用就是,实时读取服务器本地磁盘的数据,将数据写入到HDFS
基础架…
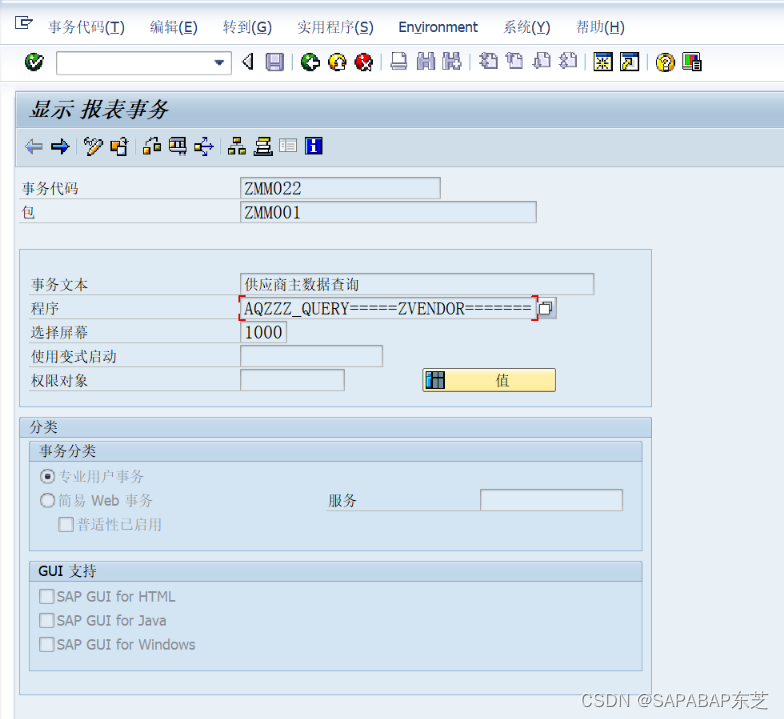
【SAP-QUERY】QUERY报表的创建
SQ03:创建用户组 环境-》查询区域-》选择标准区域 创建用户组和用户组描述 可选分配权限(授权当前用户组下人员可以修改该query报表) SQ02:创建信息集 确认区域是否为标准区域 选择创建的用户组 创建信息集:输入描述&a…
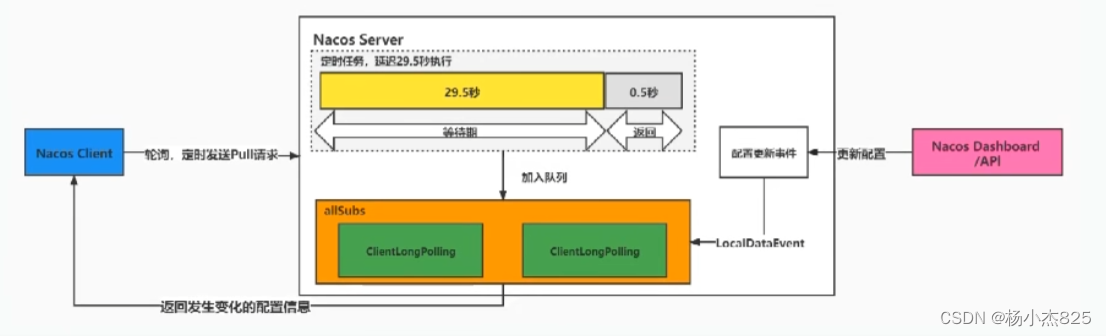
Nacos 配置中心底层原理(1.X版本)
前言 Nacos 1.X版本 是长轮询 Nacos 2.X版本 是GRPC 长轮询 概念 客户端会轮询向服务端发出一个长连接请求,这个长连接最多30s就会超时,服务端收到客户端的请求会先判断当前是否有配置更新,有则立即返回,如果没有服务端会将这个…
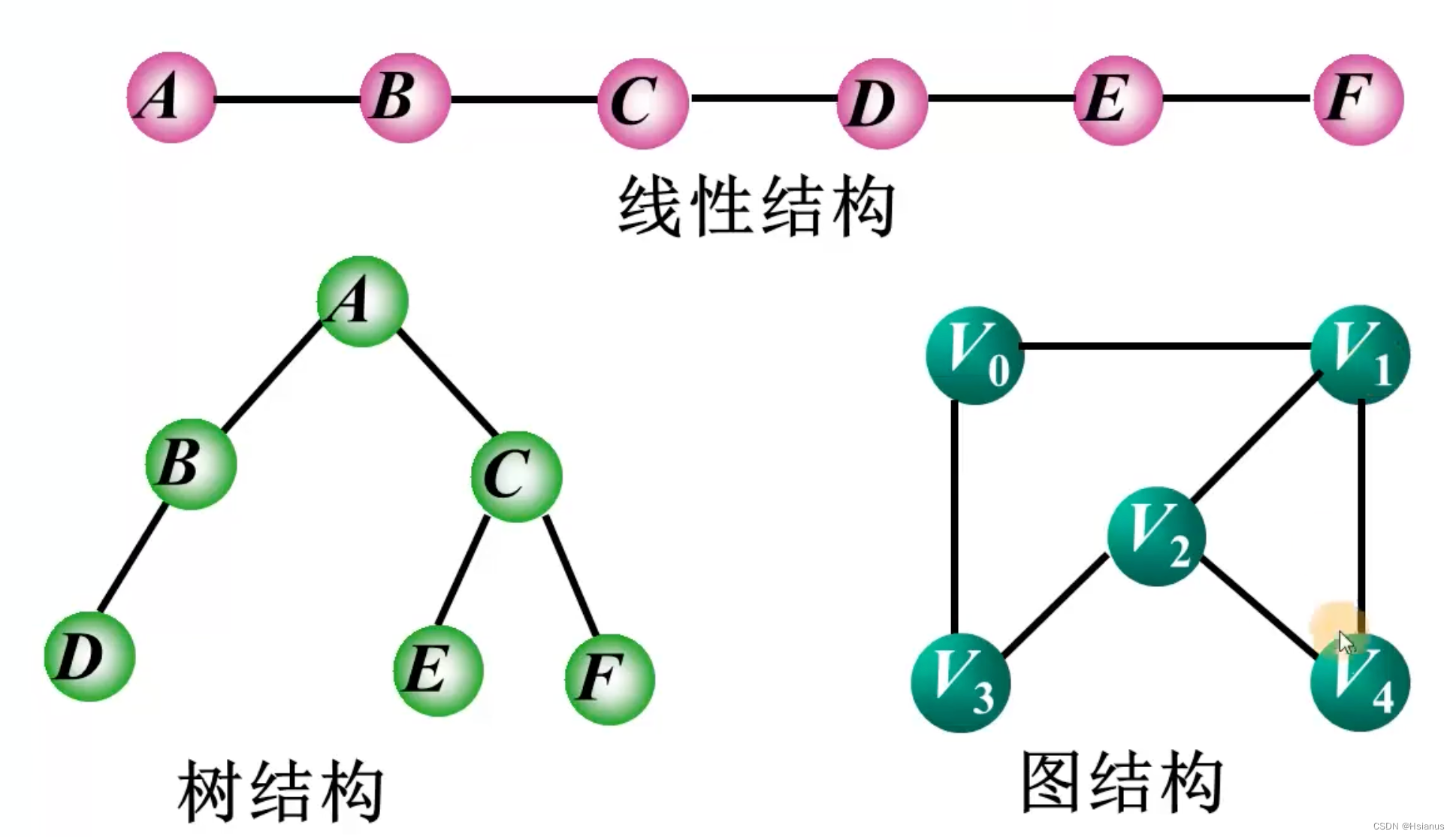
【数据结构】图的简介(图的逻辑结构)
一.引例(哥尼斯堡七桥问题) 哥尼斯堡七桥问题是指在哥尼斯堡市(今属俄罗斯)的普雷格尔河(Pregel River)中,是否可以走遍每座桥一次且仅一次,最后回到起点的问题。这个问题被认为是图…