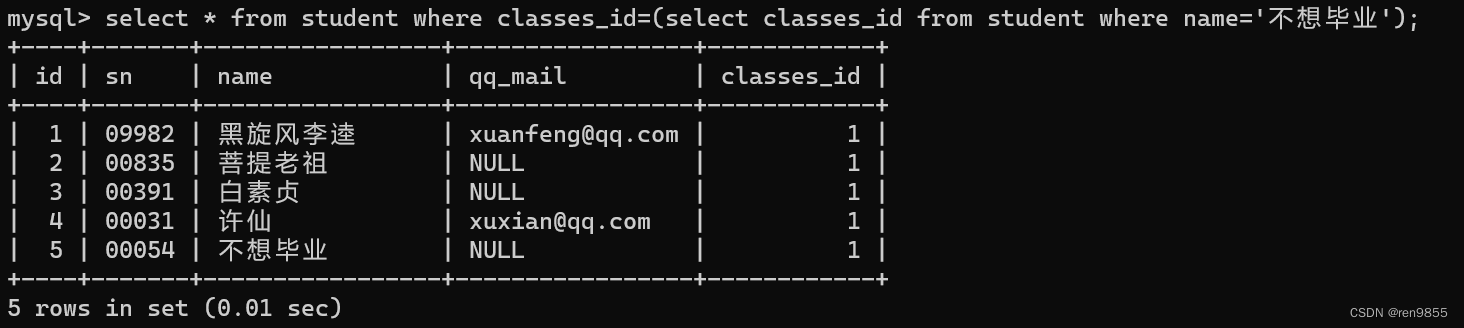
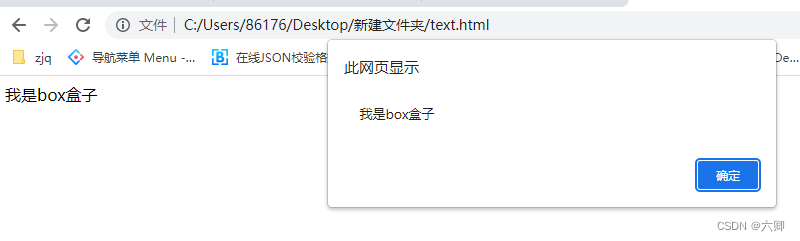
前段时间阅读了youtube的经典论文《Deep Neural Networks for YouTube Recommendations》，其通过weighted LR来实现时长预估，在其原文中对实现的描述非常短，大概意思是在损失函数中，对正例（点击）的交叉熵项，添加观看时长作为权重，会使得LR预估的odds=
能代表观看时长，即
可以表示对观看时长的预估，这篇论文很多博文都分析烂大街了，但对于weighted LR来实现时长预估的原理，很多博主分析都很有问题，或者分析似是而非，本文将会从最本质来说明其实现思想。
The model is trained with logistic regression under crossentropy loss . However, the positive (clicked) impressions are weighted by the observed watch time on the video. Negative (unclicked) impressions all receive unit weight. In this way, the odds learned by the logistic regression are
, where
is the number of training examples,
is the number of positive impressions, and
is the watch time of the ith impression. Assuming the fraction of positive impressions is small (which is true in our case), the learned odds are approximately
, where
is the click probability and
is the expected watch time of the impression. Since
首先要说明的一点的是，基础LR主要是解决分类问题的概率p估计，假设对于一个二分类问题，模型的目标是预估label=1的概率p，其结构大概分成两个部分：
- 通过线性回归拟合几率，其中
表示的是几率，
表示的模型的参数，
表示输入(式1)：
- 通过sigmord函数转换为p值(式2)：
- 模型的优化目标(式3)：
- 其损失函数可以表示为，即交叉熵函数(式4)：
说完了基本LR的形式，我们回到Youtube的weighted LR的情况下，其主要是在交叉熵Loss函数添加了权重值，即正例用观看时长作为权重值，负例的权重值为1，如下label我直接用
表示(式5)：
在论文中简单说明了下，如果损失函数通过这种权重设计后，经过训练，LR的输出就由原来的(式1)变为(式6)：
此处的tp表示对时长期望的预估，在p值远小于1的情况下，存在如下的近似形式(式7)，即
可以表示对观看时长的预估。
现在最大的问题是，如何由带权重值的Loss(式5)推导出(式6)的结果：
- 假设(式6)经过sigmord函数转换为(式8)
- 此时我们对比(式8)和(式2)，在新weighted LR模型下，预估的label由变成了t * label，而负例仍为1-label，此时还是二分类问题，只是预估的label有变化，因此我们的优化目标变成如下(式9)
- 其损失函数可以表示为(式9)，即同(式5)的形式：
总结：youtube采用weighted LR对时长进行预估的方式，实在是非常巧妙。对于时长等连续值预估的回归模型一直以来都相对复杂，而youtube仅仅只是通过调整损失函数的正例项权重值，就将原来由对点击率预估转换为对时长的预估，这里面虽然看起来简单，其中的一些细节值得反复思考。
