LFU 的设计与实现

作者：Grey

原文地址：

博客园：LFU 的设计与实现

CSDN：LFU 的设计与实现

题目描述

LFU（least frequently used）。即最不经常使用页置换算法。

题目链接：LeetCode 460. LFU Cache

主要思路

首先，定义一个辅助数据结构 Node

    public static class Node {
      public Integer key;
      public Integer value;
      public Integer times; // 这个节点发生get或者set的次数总和
      public Node up; // 节点之间是双向链表所以有上一个节点
      public Node down; // 节点之间是双向链表所以有下一个节点

      public Node(int k, int v, int t) {
        key = k;
        value = v;
        times = t;
      }
    }

这个 Node 用于封装 LFU Cache 每次加入的元素，其中 key 和 value 两个变量记录每次加入的 KV 值，times 用于记录该 KV 值被操作（get/set）的次数之和， up 和 down 两个变量用于链接和 KV 出现词频一样的数据项，用链表串联。

接下来需要另外一个辅助数据结构 NodeList，前面的 Node 结构已经把词频一致的数据项组织在同一个桶里，这个 NodeList 用于连接出现不同词频的桶，用双向链表组织

    public static class NodeList {
      public Node head; // 桶的头节点
      public Node tail; // 桶的尾节点
      public NodeList last; // 桶之间是双向链表所以有前一个桶
      public NodeList next; // 桶之间是双向链表所以有后一个桶

      public NodeList(Node node) {
        head = node;
        tail = node;
      }
      ……
    }

使用一个具体的示例来表示上述两个结构如何组织的

例如，LFU Cache 在初始为空的状态下，进来如下数据

key = A, value = 3

key = B, value = 30

key = C, value = 4

key = D, value = 12

那么 LFU 会做如下组织

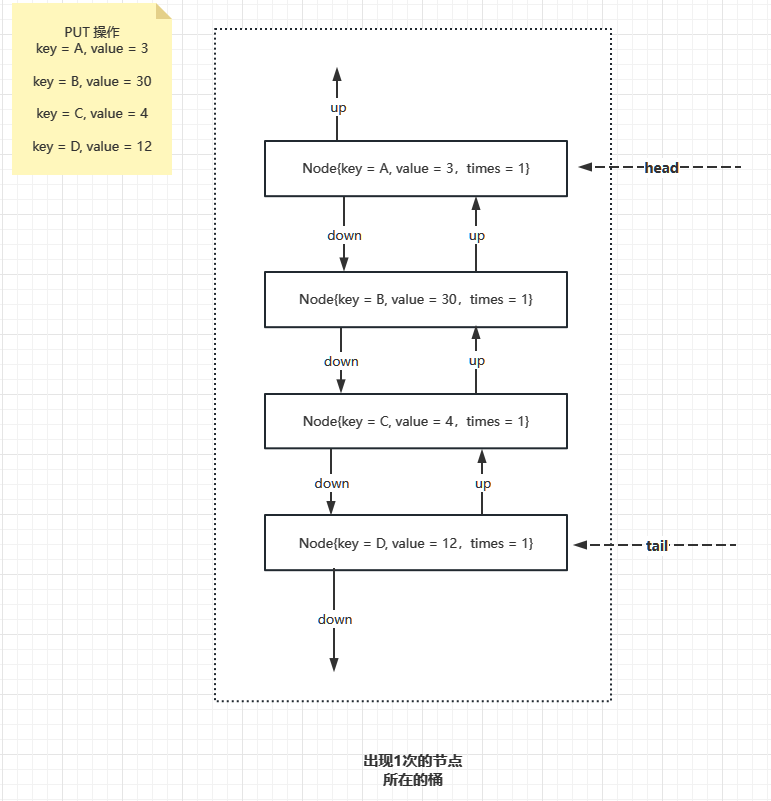
此时只有出现一次的桶，接下来，如果 key = C 这条记录被访问过了，所以词频变为2，接下来要把 key = C 这条记录先从词频为1的桶里面取出来，然后再新建一个词频为 2 的桶，把这个 key = C 的数据项挂上去，结果如下

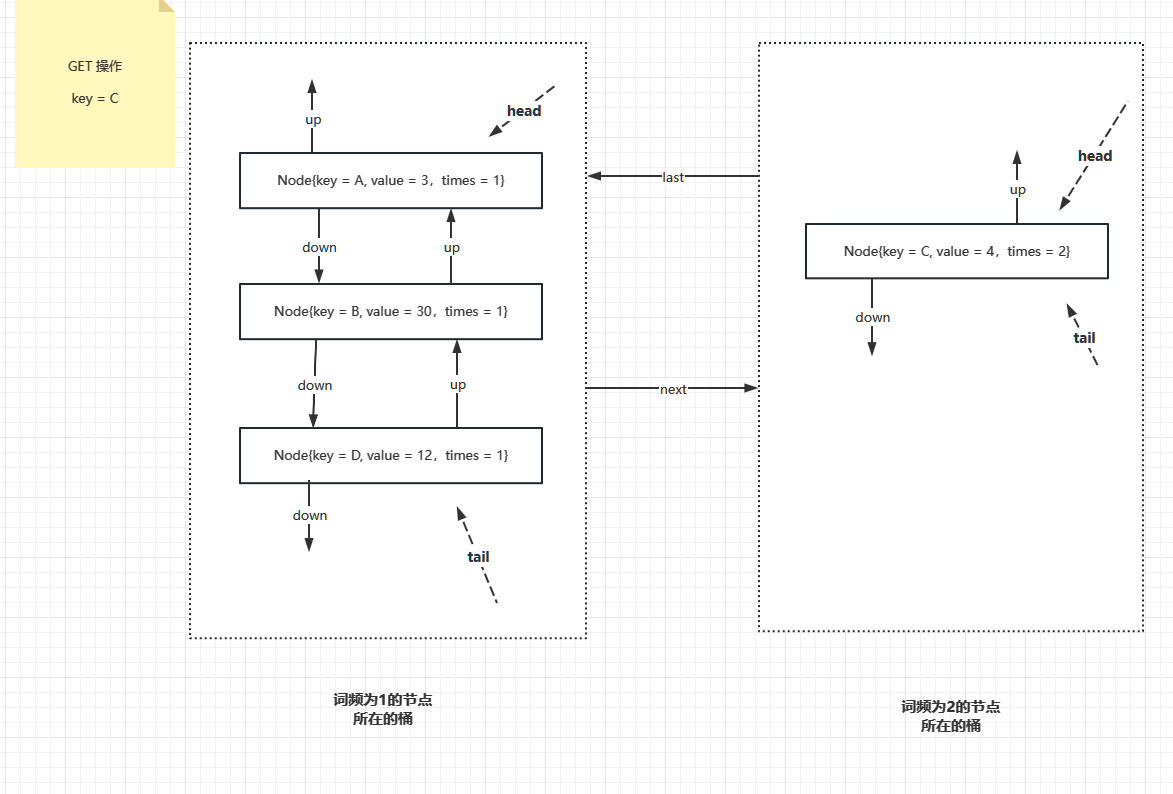
接下来，如果又操作了 key = C 这条记录，那么这条记录的词频就是 3，又需要新增一个词频为 3 的桶，原来词频为 2 的桶已经没有数据项了，要销毁，并且把词频为 1 的桶和词频为 3 的桶连接在一起。

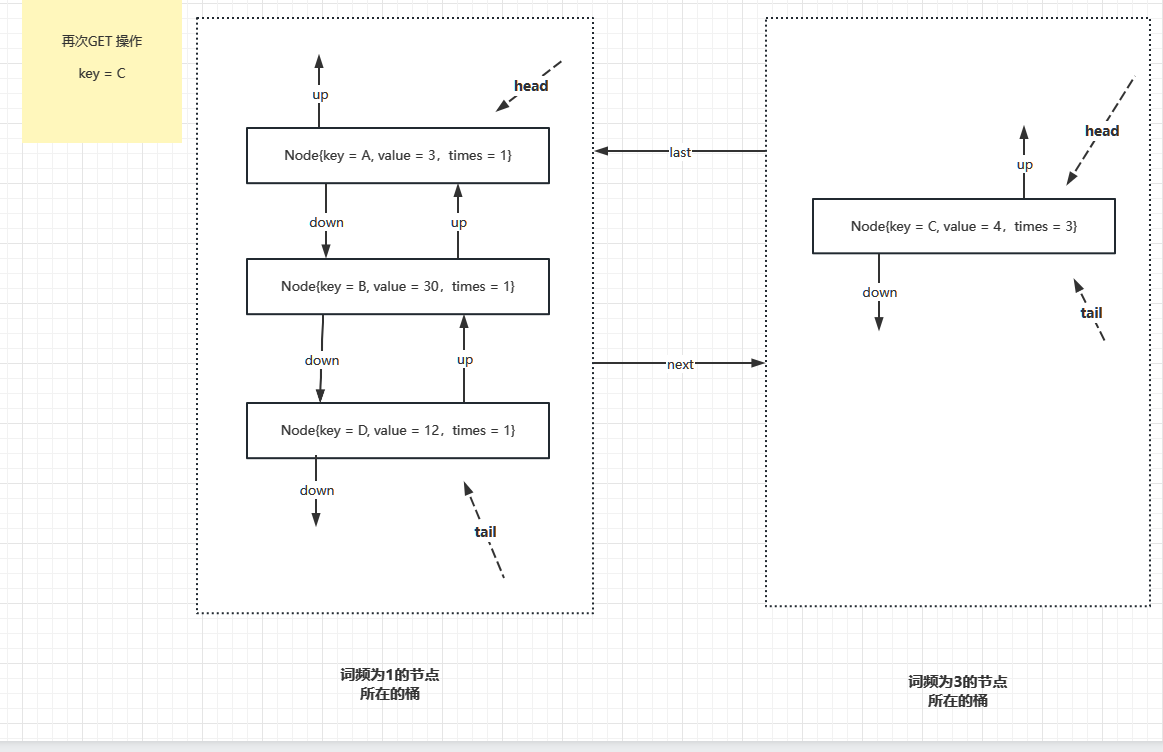
接下来，如果操作了 key = A，则 key = A 成为词频为 2 的数据项，再次新增词频为 2 的桶，并把这个桶插入到词频为 1 和词频为 3 的桶之间，如下图

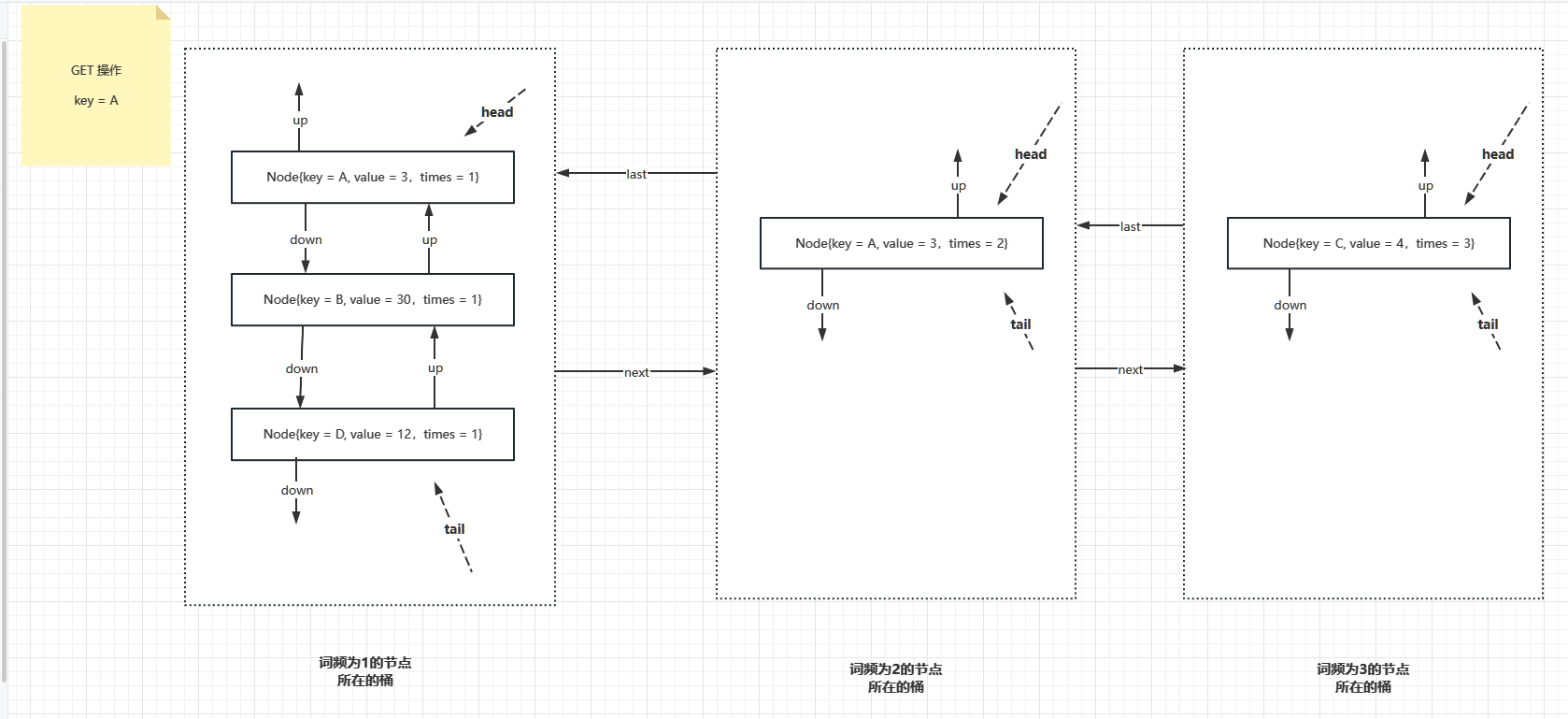
以上示例就可以很清楚说明了 Node 和 NodeList 两个数据结构在 LFU 中的作用，接下来，为了实现快速的 put 和 get 操作，需要定义如下成员变量

int capacity; // 缓存的大小限制
int size; // 缓存目前有多少个节点
HashMap<Integer, Node> records; // 表示key(Integer)由哪个节点(Node)代表
HashMap<Node, NodeList> heads; // 表示节点(Node)在哪个桶(NodeList)里
NodeList headList; // 整个结构中位于最左的桶，是一个双向链表

说明：records 这个变量就是用于快速得到某个 key 的节点（Node）是什么，由于这里的 kv 都是整型，所以用 Integer 作为 key 可以定位到对应的 Node 数据项信息。

heads 则用于快速定位某个 Node 在哪个桶里面。

headList 表示整个结构中位于最左侧的桶，这个桶一定是出现次数最少的桶，所以淘汰的时候，优先淘汰这个桶里面的末尾位置，即 tail 位置的 node！

两个核心方法 put 和 get 的核心代码说明如下

    public void put(int key, int value) {
      
      if (records.containsKey(key)) {
// put 的元素是已经存在的
// 更新元素值，更新出现次数
        Node node = records.get(key);
        node.value = value;
        node.times++;
        // 通过heads以O(1)复杂度定位到所在的桶
        NodeList curNodeList = heads.get(node);
        // 把这个更新后的 Node 从 旧的桶迁移到新的桶
        move(node, curNodeList);
      } else {
        if (size == capacity) {
            // 容量已经满了
            // 淘汰 headList 尾部的节点！因为这个节点是最久且最少用过的节点
          Node node = headList.tail;
          headList.deleteNode(node);
          // 删掉的节点有可能会让 headList 换头，因为最右侧的桶可能只有一个节点，被删除后，就没有了。
          modifyHeadList(headList);
          // records和 heads 中都要删掉其记录
          records.remove(node.key);
          heads.remove(node);
          size--;
        }
        // 以上操作就是淘汰了一个节点
        // 接下来就放心加入节点
        // 先建立Node，词频设置为 1
        Node node = new Node(key, value, 1);
        if (headList == null) {
            // 如果headList为空，说明最左侧的桶没有了，新来节点正好充当最左侧节点的桶中元素
          headList = new NodeList(node);
        } else {
          if (headList.head.times.equals(node.times)) {
            // 最右侧桶不为空的情况下，这个节点出现的次数又正好等于最左侧桶所代表的节点数
            // 则直接加入最左侧桶中
            headList.addNodeFromHead(node);
          } else {
            // 将加入的节点作为做左侧桶，接上原先的headList
            // eg：新加入的节点出现的次数是1，原先的 headList代表的桶是词频为2的数据
            // 就会走这个分支
            NodeList newList = new NodeList(node);
            newList.next = headList;
            headList.last = newList;
            headList = newList;
          }
        }
        records.put(key, node);
        heads.put(node, headList);
        size++;
      }
    }

    public int get(int key) {
      if (!records.containsKey(key)) {
        // 不包含这个key
        // 按题目要求直接返回 -1
        return -1;
      }
      // 否则，先取出这个节点
      Node node = records.get(key);
      // 词频+1
      node.times++;
      // 将这个节点所在的桶找到
      NodeList curNodeList = heads.get(node);
      // 将这个节点从原桶调整到新桶
      move(node, curNodeList);
      return node.value;
    }

PS：这里涉及的对双向链表和桶链表的两个操作move和modifyHeadList逻辑不难，但是很多繁琐的边界条件要处理，具体方法的说明见上述代码注释，不赘述。

完整代码如下

static class LFUCache {

    private int capacity; // 缓存的大小限制
    private int size; // 缓存目前有多少个节点
    private HashMap<Integer, Node> records; // 表示key(Integer)由哪个节点(Node)代表
    private HashMap<Node, NodeList> heads; // 表示节点(Node)在哪个桶(NodeList)里
    private NodeList headList; // 整个结构中位于最左的桶

    public LFUCache(int capacity) {
      this.capacity = capacity;
      size = 0;
      records = new HashMap<>();
      heads = new HashMap<>();
      headList = null;
    }

    // 节点的数据结构
    public static class Node {
      public Integer key;
      public Integer value;
      public Integer times; // 这个节点发生get或者set的次数总和
      public Node up; // 节点之间是双向链表所以有上一个节点
      public Node down; // 节点之间是双向链表所以有下一个节点

      public Node(int k, int v, int t) {
        key = k;
        value = v;
        times = t;
      }
    }

    // 桶结构
    public static class NodeList {
      public Node head; // 桶的头节点
      public Node tail; // 桶的尾节点
      public NodeList last; // 桶之间是双向链表所以有前一个桶
      public NodeList next; // 桶之间是双向链表所以有后一个桶

      public NodeList(Node node) {
        head = node;
        tail = node;
      }

      // 把一个新的节点加入这个桶，新的节点都放在顶端变成新的头部
      public void addNodeFromHead(Node newHead) {
        newHead.down = head;
        head.up = newHead;
        head = newHead;
      }

      // 判断这个桶是不是空的
      public boolean isEmpty() {
        return head == null;
      }

      // 删除node节点并保证node的上下环境重新连接
      public void deleteNode(Node node) {
        if (head == tail) {
          head = null;
          tail = null;
        } else {
          if (node == head) {
            head = node.down;
            head.up = null;
          } else if (node == tail) {
            tail = node.up;
            tail.down = null;
          } else {
            node.up.down = node.down;
            node.down.up = node.up;
          }
        }
        node.up = null;
        node.down = null;
      }
    }
    private boolean modifyHeadList(NodeList removeNodeList) {
      if (removeNodeList.isEmpty()) {
        if (headList == removeNodeList) {
          headList = removeNodeList.next;
          if (headList != null) {
            headList.last = null;
          }
        } else {
          removeNodeList.last.next = removeNodeList.next;
          if (removeNodeList.next != null) {
            removeNodeList.next.last = removeNodeList.last;
          }
        }
        return true;
      }
      return false;
    }


    private void move(Node node, NodeList oldNodeList) {
      oldNodeList.deleteNode(node);
      NodeList preList = modifyHeadList(oldNodeList) ? oldNodeList.last : oldNodeList;
      NodeList nextList = oldNodeList.next;
      if (nextList == null) {
        NodeList newList = new NodeList(node);
        if (preList != null) {
          preList.next = newList;
        }
        newList.last = preList;
        if (headList == null) {
          headList = newList;
        }
        heads.put(node, newList);
      } else {
        if (nextList.head.times.equals(node.times)) {
          nextList.addNodeFromHead(node);
          heads.put(node, nextList);
        } else {
          NodeList newList = new NodeList(node);
          if (preList != null) {
            preList.next = newList;
          }
          newList.last = preList;
          newList.next = nextList;
          nextList.last = newList;
          if (headList == nextList) {
            headList = newList;
          }
          heads.put(node, newList);
        }
      }
    }

    public void put(int key, int value) {
      if (capacity == 0) {
        return;
      }
      if (records.containsKey(key)) {
        Node node = records.get(key);
        node.value = value;
        node.times++;
        NodeList curNodeList = heads.get(node);
        move(node, curNodeList);
      } else {
        if (size == capacity) {
          Node node = headList.tail;
          headList.deleteNode(node);
          modifyHeadList(headList);
          records.remove(node.key);
          heads.remove(node);
          size--;
        }
        Node node = new Node(key, value, 1);
        if (headList == null) {
          headList = new NodeList(node);
        } else {
          if (headList.head.times.equals(node.times)) {
            headList.addNodeFromHead(node);
          } else {
            NodeList newList = new NodeList(node);
            newList.next = headList;
            headList.last = newList;
            headList = newList;
          }
        }
        records.put(key, node);
        heads.put(node, headList);
        size++;
      }
    }

    public int get(int key) {
      if (!records.containsKey(key)) {
        return -1;
      }
      Node node = records.get(key);
      node.times++;
      NodeList curNodeList = heads.get(node);
      move(node, curNodeList);
      return node.value;
    }
  }