目录
从词向量到实体向量
知识图谱向量表示学习模型
TransE
TransH
TransR
TransD
TransX系列总结
DisMult
从词向量到实体向量
知识图谱的向量表示。有一类词是代表实体的,假如对这类实体词的向量做一些计算,比如用Rome向量减去Italy的向量,会发现这个差值和用Paris的向量减去France的向量比较接近。这里的原因是Rome和Italy之间,以及Paris和France之间都存在is-capital-of的关系,如下图所示。这里看到了熟悉的知识图谱<主语, 谓语, 宾语>三元组结构。这启发可以利用三元组结构来学习知识图谱中实体和关系的向量表示,就像可以利用句子中词的上下文共现关系来学习词的向量表示一样。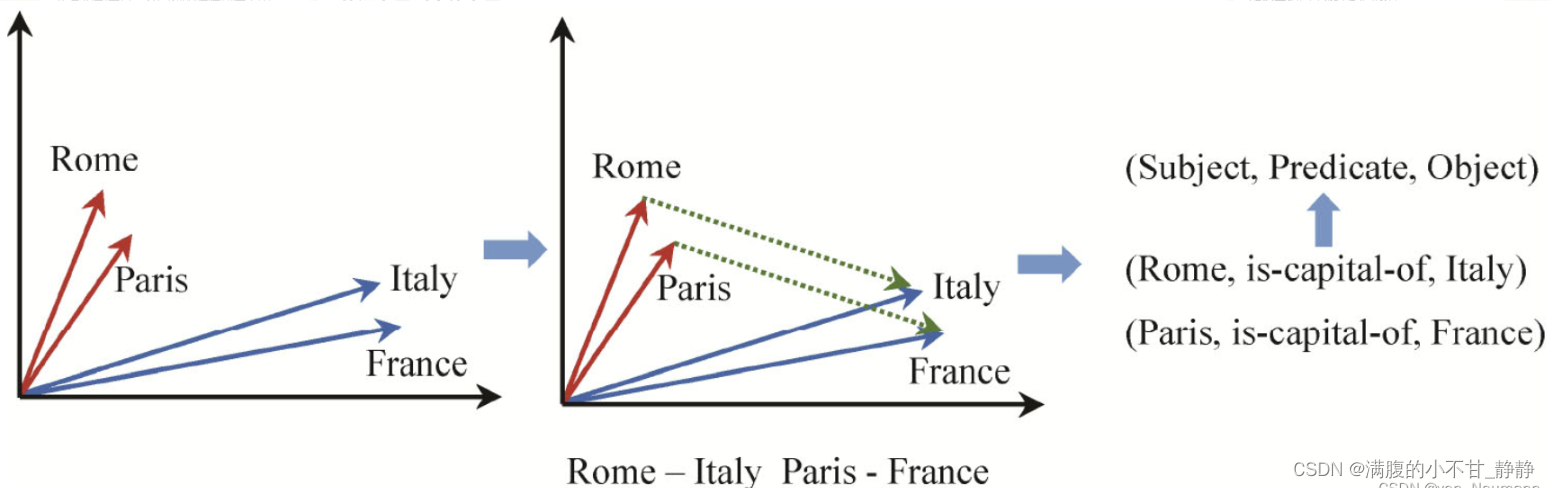
知识图谱向量表示学习模型
TransE
标题:Translating Embeddings for Modeling Multi-relational Data(2013)
有很多这样利用主谓宾三元组结构来学习知识图谱中实体和关系的向量表示的模型,其中一个比较简单但有效的模型是TransE。这是转换模型系列的第一部作品。该模型的基本思想是使head向量和relation向量的和尽可能靠近tail向量。这里我们用L1或L2范数来衡量它们的靠近程度。
它的想法很简单,给定一个三元组<h,r,t>,其中h代表head,即主语(subject),r代表relation,即关系谓词,t代表tail,即宾语(Object),如果它所代表的事实是客观存在的,那么h、r、t的向量表示应该满足加法关系h+r=t。例如Rome+is-capital of应该在向量空间接近于Italy;Paris+is-capital-of的结果也应该接近于France,如下图所示: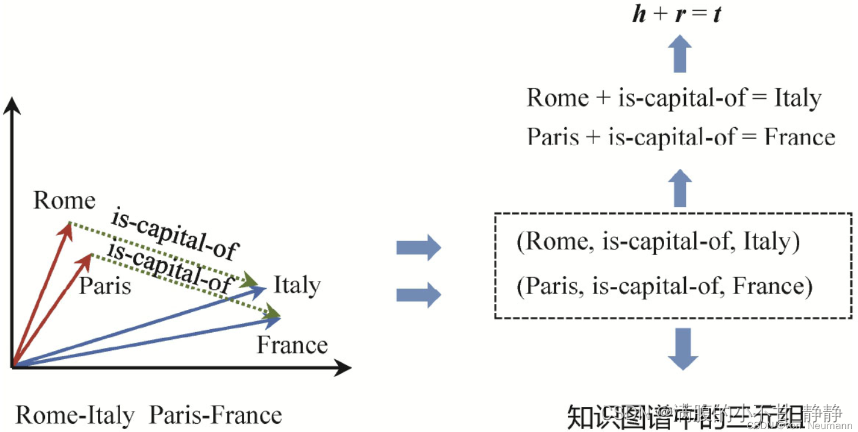
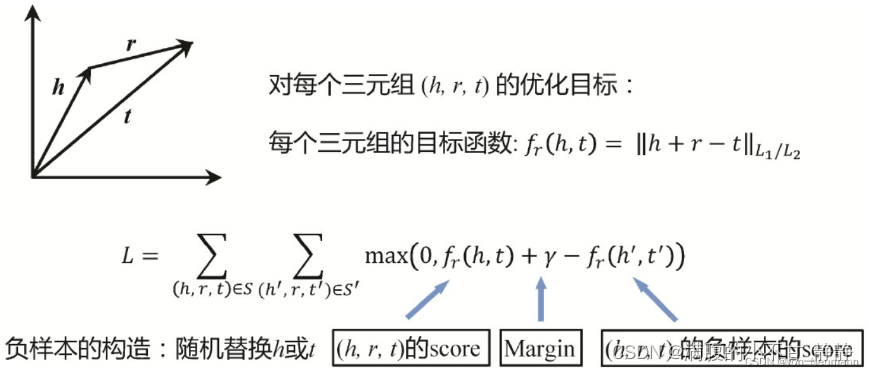
对于每一个三元组,可以定义一个评分函数,然后对所有的三元组累加计算损失函数L ,如下图所示。例如给定Margin Loss的定义,这里的优化目标就是让真实存在的三元组得分尽可能高,而让不存在的三元组的得分尽可能低。可以采用简单的梯度下降优化方法,例如,可以随机初始化所有实体和关系的向量表示,然后一轮一轮地优化这些向量中的参数。如果优化目标能够收敛,最后学习到的绝大部分实体和关系的向量表示就应该满足h+r=t的假设。这里的负样本,也就是不存在的三元组可以有很多种方法构建,一种方法是随机地替换真实三元组的头尾实体,这些新生成的三元组大部分是不存在的,因而可以作为模型的负样本。
缺点:这个模型只能处理一对一的关系,不适合一对多/多对一关系,例如,有两个知识,(skytree, location, tokyo)和(gundam, location, tokyo)。经过训练,“sky tree”实体向量将非常接近“gundam”实体向量。但实际上它们没有这样的相似性。
主要原因是因为模型过于简单,在对1-N、N-1、N-N等复杂关系进行建模时,我们可以推出以下结论:
如果关系r是N-1关系,我们将会得到 lh0≈lh1≈...≈lhm 同样的,这样的问题在关系r是N-1关系时也会发生,得到 lt0≈lt1≈...≈ltm 具体来说,例如在知识库中有两个三元组,分别是(美国, 总统, 奥巴马)和(美国, 总统, 布什)。这里的关系“总统”是典型的1-N负责关系,如果用TransE模型从这两个三元组学习知识表示,将会使奥巴马和布什的向量变得相同,这显然不符合事实。
TransH
标题: Knowledge Graph Embedding by Translating on Hyperplanes(2014)
TransH的目标是处理一对多/多对一/多对多关系,并且不增加模式的复杂性和训练难度。
其基本思想是将关系解释为超平面上的转换操作。每个关系都有两个向量,超平面的范数向量Wr和超平面上的平移向量(dr)。
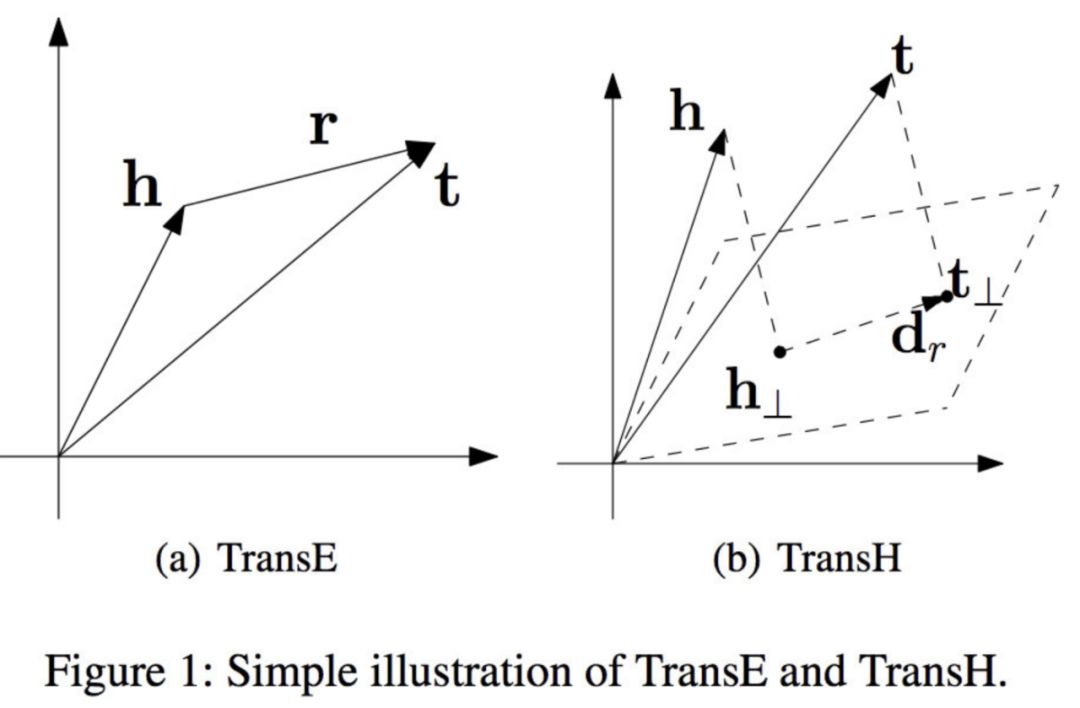
我们把每个head向量(h)和tail向量(t)投影到超平面上,得到新的向量(h⊥和t⊥)。在这个超平面中存在一个关系(d_r),我们可以像TransE模型一样训练它。
![]()
得分函数:
![]()
如何在超平面上计算这个投影:
![]()
其中w_r的范数约束为1。
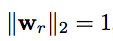
h⊥ 是h在超平面上的投影,wrT是h在wr上的投影。这意味着我们将head/tail向量分解为两部分。
![]()
损失函数和训练方法与TransE相同。

我们把head/tail向量分解两部分,只使用一个部分(h⊥或t⊥)来训练模型。这可以避免在模型训练时两个实体(head或tail)接近,并处理一对多/多对一/多对多关系。
缺点:
TransE和TransH模型都假设实体和关系是语义空间中的向量,因此相似的实体在同一实体空间中会非常接近。然而,每个实体可以有许多方面,不同的关系关注实体的不同方面。例如,(location, contains, location)的关系是'contains',(person, born, date)的关系是'born'。这两种关系非常不同。
TransR
标题: Learning Entity and Relation Embeddings for Knowledge Graph Completion(2015)
为了解决TransH的问题,我们让TransR在两个不同的空间,即实体空间和多个关系空间(关系特定的实体空间)中建模实体和关系,并在对应的关系空间中进行转换,因此命名为TrandR。
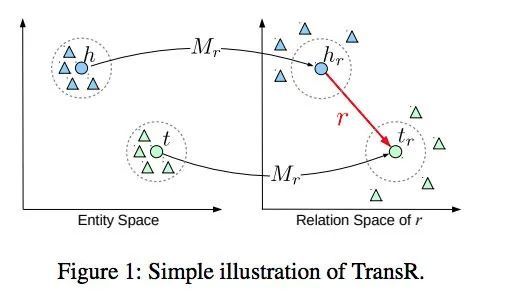
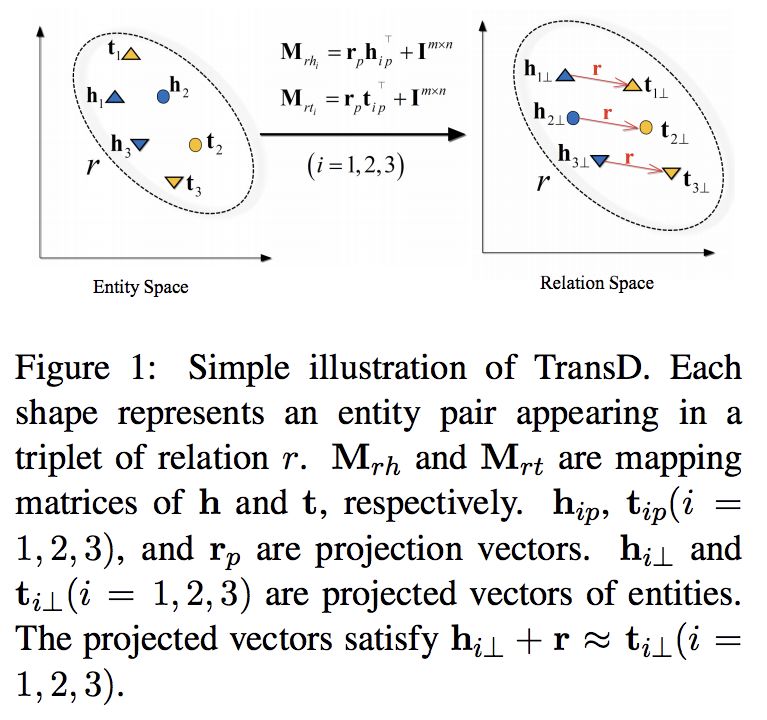
TransR的基本思想如图1所示。对于每个三元组(h, r, t),将实体空间中的实体通过矩阵Mr投影到r关系空间中,分别为hr和tr,然后有hr + r ≈ tr,损失函数和训练方法与TransE相同。h和t为实体嵌入,r为关系嵌入。
![]()
特定于关系的投影可以使实际持有这种关系的head/tail实体(表示为彩色圆圈)彼此靠近,同时那些不持有这个关系的实体相互远离(表示为彩色三角形)。
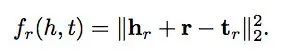
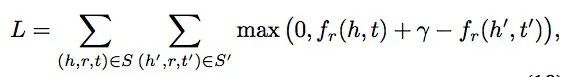
得分函数和目标函数与TransE相同。
TransR有一个变体模型,称为CTransR, C表示聚类。head和tail实体通常呈现不同的模式。仅仅构建一个关系向量来执行从head到tail实体的所有转换是不够的。例如,三元组(location, contains, location)具有许多模式,如country-city、country-university、contin- country等等。为了解决这个问题,CTransR将不同的head和tail实体对进行聚类,并对每一组学习不同的关系向量。
构造CtransR的过程是,对于一个特定的关系r,将训练数据中所有的实体对*(h, t)聚类到多个组中,期望每组中的实体对呈现相似的r关系。我们使用向量偏移量(h-t)表示实体对(h, t)*。我们从TransE得到h和t。然后,我们分别学习了每个聚类对应的关系向量r_c,每个关系对应的矩阵Mr。
缺点:
- 首先,head和tail使用相同的转换矩阵将自己投射到超平面上,但是head和tail通常是一个不同的实体,例如,
(Bill Gates, founder, Microsoft)。'Bill Gate'是一个人,'Microsoft'是一个公司,这是两个不同的类别。所以他们应该以不同的方式进行转换。 - 第二,这个投影与实体和关系有关,但投影矩阵仅由关系决定。
- 最后,TransR的参数数大于TransE和TransH。由于其复杂性,TransR/CTransR难以应用于大规模知识图谱。
TransD
标题: Knowledge Graph Embedding via Dynamic Mapping Matrix(2015)
TransD使用两个向量来表示每个实体和关系。第一个向量表示实体或关系的意义,另一个向量(称为投影向量)将用于构造映射矩阵。
两个映射矩阵定义如下:

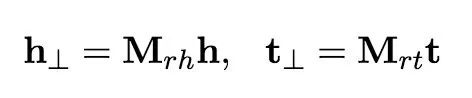
其中映射矩阵由实体和关系定义,I为单位矩阵。这个等式意味着我们使用生成的矩阵(由r和h向量)来修改单位矩阵。投射和训练与TransR相同。
TransE是向量维数满足m=n且所有投影向量都设为零时变换的一种特殊情况。
TransX系列总结


margin loss适用于所有模型。这些模型都是基于分段的,利用head向量和relation向量的和来预测tail向量。这些模型的不同之处在于它们使用不同的方法来表示实体/关系向量。
DisMult



![[Python学习系列] 走进Django框架](https://img-blog.csdnimg.cn/25df00b39891417a80e9463099c351ae.png)