题目

给你一个用字符数组 tasks 表示的 CPU
需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行，并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间，CPU 可以完成一个任务，或者处于待命状态。

然而，两个 相同种类 的任务之间必须有长度为整数 n 的冷却时间，因此至少有连续 n 个单位时间内 CPU在执行不同的任务，或者在待命状态。

你需要计算完成所有任务所需要的 最短时间 。

思路

构造题（脑筋急转弯）

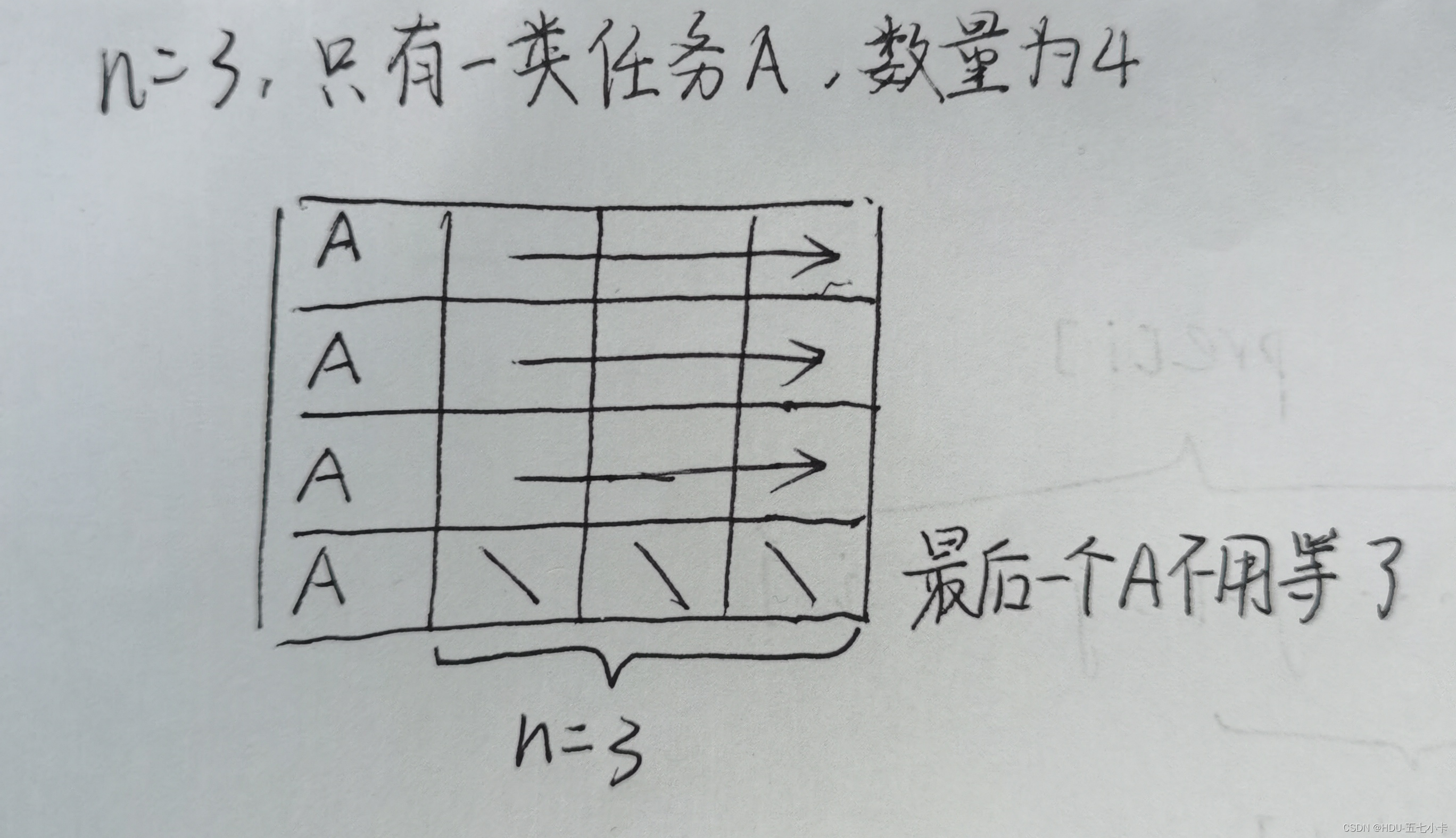
先考虑最为简单的情况：假设只有一类任务，除了最后一个任务以外，其余任务在安排后均需要增加 n 个单位的冻结时间。

将任务数记为 m 个，其中前 m−1个任务均要消耗 n+1 的单位时间，最后一个任务仅消耗 1 个单位时间，即所需要的时间为 (n+1) * (m−1)+1。

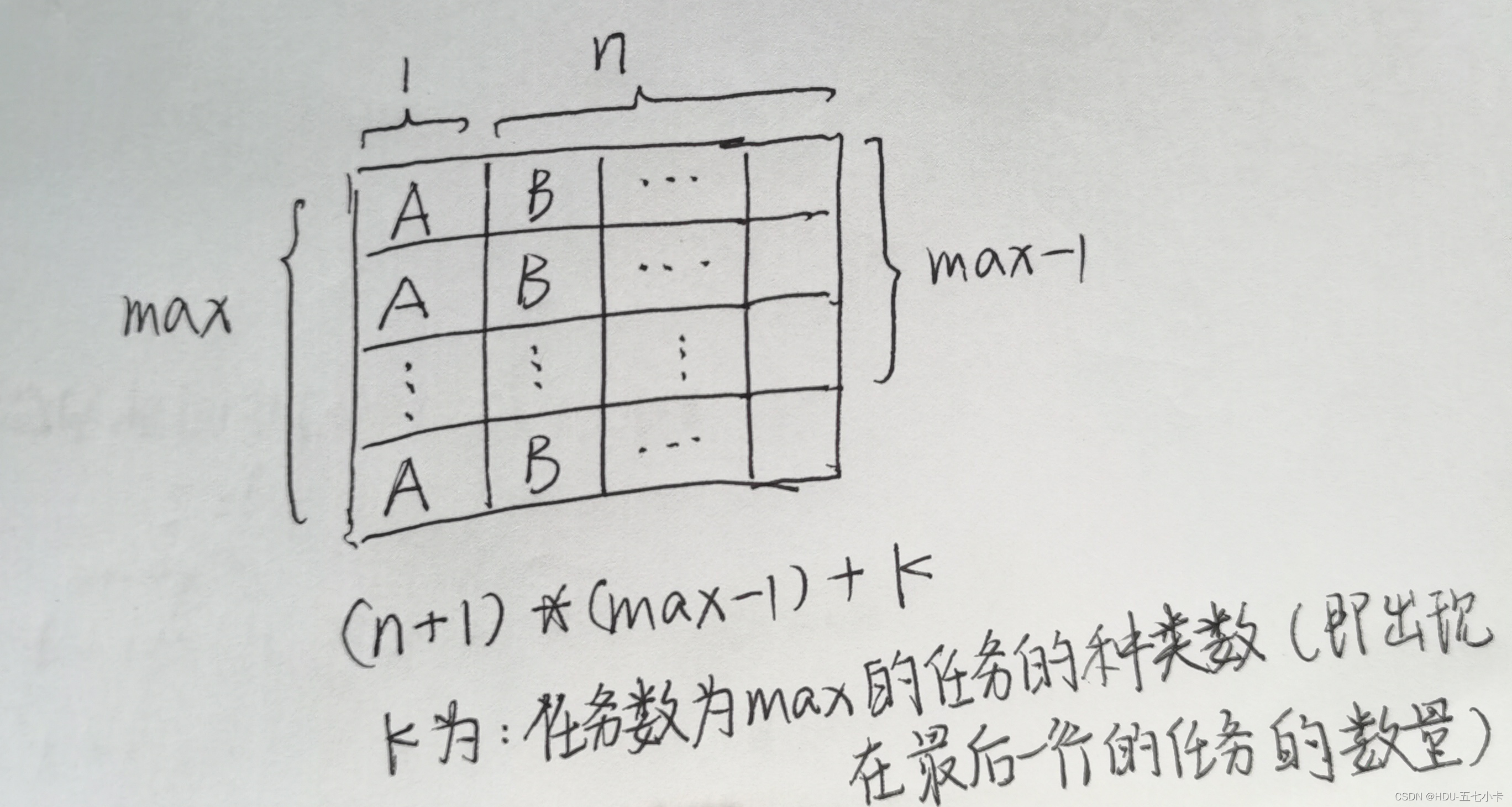
当存在多个任务时，由于每一类任务都需要被完成，因此本质上最需要考虑的是将数量最大的任务安排掉，其他任务则是间插其中。

假设数量最大的任务数为 max，共有 k个任务数为 max 的任务种类。

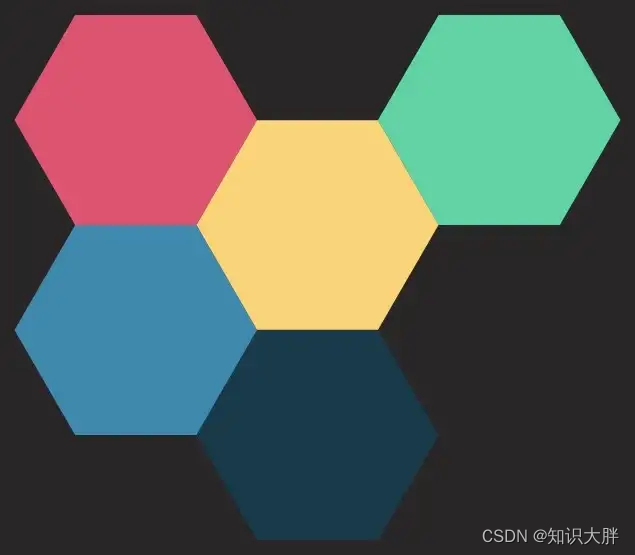
实际上，当任务总数不超过 (n+1) * (max⁡−1)+k时，总能将其他任务插到空闲时间中去，不会引入额外的冻结时间（下左图）；而当任务数超过该值时，可以在将其横向添加每个 n+1 块的后面，同时不会引入额外的冻结时间（下右图）：

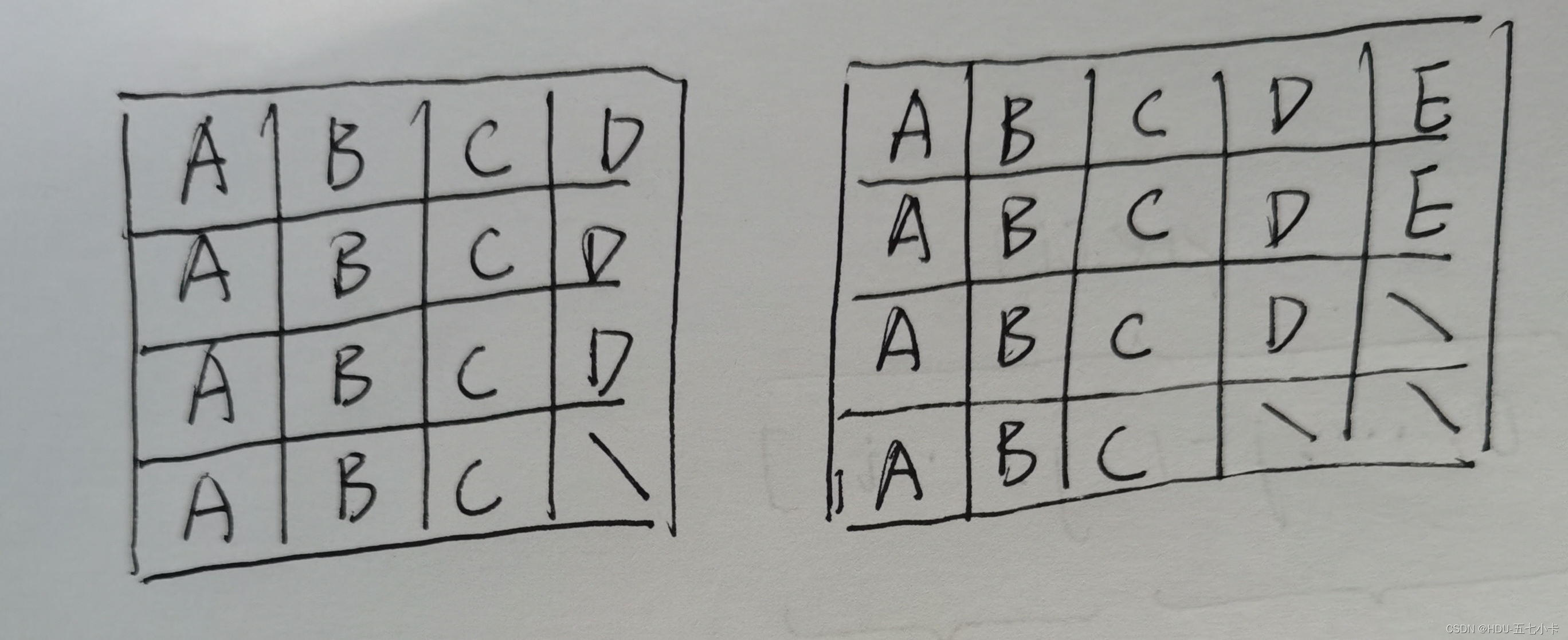
综上，所需要的最小时间为上述两种情况中的较大值即可：

Math.max⁡(task.length, (n+1) * (max−1) + k)

java代码如下：

class Solution {
    public int leastInterval(char[] tasks, int n) {
        int[] cnts = new int[26];//用数组充当哈希表的作用
        for (char c : tasks) cnts[c - 'A']++;//将任务中的每个任务存在哈希表中，并统计出现的次数即，任务数
        int max = 0, k = 0;//max—数量最多的任务数，k—数量为max的任务种类数，比如A.B任务都是max个，则k为2
        for (int i = 0; i < 26; i++) 
        	max = Math.max(max, cnts[i]);//遍历哈希表，找出任务数最多的max
        for (int i = 0; i < 26; i++) 
        	k += max == cnts[i] ? 1 : 0;//遍历哈希表，找出任务数为max的任务种类数k
        return Math.max(tasks.length, (n + 1) * (max - 1) + k);
    }
}