文章目录
- 第一节:选择排序
- 1. 选择排序原理解析
- 2. 选择排序代码实战
- 3. 时间复杂度与空间复杂度
- 第二节:堆排序
- 1. 堆排序原理解析
- 2. 堆排序代码实战
- 3. 时间复杂度与空间复杂度
- 第三节:归并排序
- 1. 归并排序原理解析
- 2. 归并排序代码实战
- 3. 时间复杂度与空间复杂度
- 第四节:小结
- 所有排序算法时间与空间复杂度汇总
第一节:选择排序
1. 选择排序原理解析
选择排序分为:1.简单选择排序。2.堆排序(重要)。
简单选择排序原理:假设排序表为L[1,2,……n],第i趟排序即从L[i……n]中选择关键字最小的元素与L(i)交换,每一趟排序可以确定一个元素的最终位置,这样经过n-1趟排序就可使得整个排序表有序。
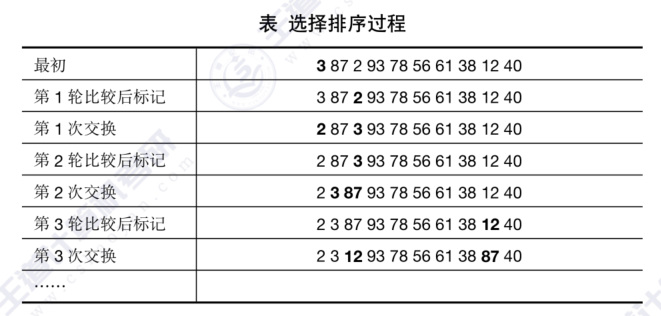
首先嘉定第0个元素是最小的,把下标0赋给min(min记录最小的元素的下标),内层比较时,从1号元素一直比较到9号元素,谁更小,就把它的下标赋给min,一轮比较结束后,将min对应的位置的元素与元素i交换。第一轮确认2最小,将2与数组开头的元素3交换,第二轮我们最初认为87最小,经过一轮比较,发现3最小,将87与3交换。持续进行,最终使数组有序。
动画演示:
https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html

2. 选择排序代码实战
步骤:随机10个元素->打印->选择排序->打印。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
typedef int ElemType;
typedef struct {
ElemType *elem; // 整型指针
int TableLen; // 存储动态数组里边元素的个数,相当于之前的len
}SSTable;
// 初始化链表
void ST_Init(SSTable &ST,int len){
ST.TableLen=len;
ST.elem= (ElemType*)malloc(sizeof(ElemType)*ST.TableLen);
int i;
srand(time(NULL));// 生成随机数
for(i=0;i<ST.TableLen;i++){
ST.elem[i]=rand()%100; // 为了让随机数在0-99之间
}
}
// 打印
void ST_print(SSTable ST){
for(int i=0;i<ST.TableLen;i++){
printf("%3d",ST.elem[i]);// 和获取数组方法一样
}
printf("\n");
}
// 交换位置
void swap(ElemType &a,ElemType &b){
ElemType tmp;
tmp=a;
a=b;
b=tmp;
}
// 选择排序
void SelectSort(ElemType A[],int n){
int i,j,min;
for(i=0;i<n-1;i++){
min=i; // 认为第i个位置最小
for(j=i+1;j<n;j++){
if(A[j]<A[min]){
min=j;
}
}
if(min!=i){
swap(A[i],A[min]);
}
}
}
int main() {
SSTable ST;
ST_Init(ST,10);
ST_print(ST);
SelectSort(ST.elem,10);
ST_print(ST);
return 0;
}
F:\Computer\Project\practice\17\17.3-selectSort\cmake-build-debug\17_3_selectSort.exe
5 8 65 13 26 38 40 65 82 97
5 8 13 26 38 40 65 65 82 97
进程已结束,退出代码为 0
3. 时间复杂度与空间复杂度
时间复杂度O( n 2 n^2 n2)。
空间复杂度O(1)。
第二节:堆排序
1. 堆排序原理解析
堆(Heap)是计算机科学中的一种特殊的树状数据结构。若满足以下特性,则可称为堆:“给定堆中任意节点P和C,若P是C的父结点,则P的值小于等于(或大于等于)C的值。”若父结点的值恒小于等于子结点的值,则该堆称为最小堆(min heap),反之,称为最大堆(max heap)。堆中最顶端的那个结点称为根结点(root node),根结点本身没有父结点(parent node)。平时工作中,我们将最小堆称为小根堆或小顶堆,把最大堆称为大根堆或大顶堆。
假设我们有3,87,2,93,78,56,61,38,12,40共10个元素,我们将这10个元素建成一棵完全二叉树,这里采用层次建树法,虽然只有一个数组存储元素,但是我们能将二叉树中任意一个位置的元素对应到数组下标上,我们将二叉树中每个元素到数组下标的这种数据结构称为堆。比如最后一个父元素的下标是n/2-1,也就是a[4],对应的值是78。可以这样记忆:如果父结点的下标是dad,那么父结点对应的左子结点的下标值是2*dad+1。接着,依次将没棵子树都调整为父结点最大,最终整棵树将变成一个大根堆。
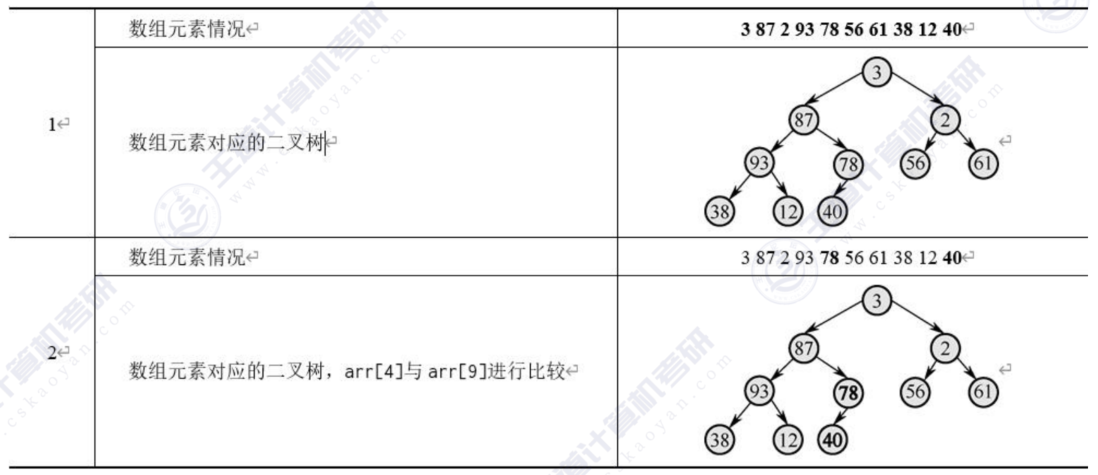
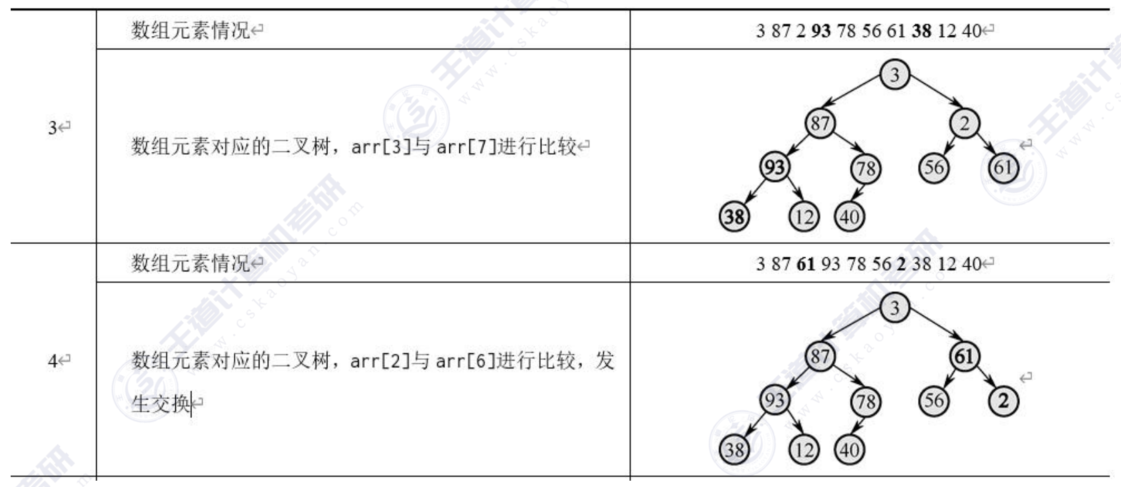

动画演示:
https://www.cs.usfca.edu/~galles/visualization/HeapSort.html
2. 堆排序代码实战
堆排序的步骤是首先把堆调整为大根堆,然后我们交换根部元素也就是A[0]和最后一个元素,这样最大的元素就放到了数组最后,接着我们将剩余9个元素继续调整成大根堆,然后交换A[0]和9个元素最后一个,循环往复,直到有序。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>
typedef int ElemType;
typedef struct {
ElemType *elem; // 整型指针
int TableLen; // 存储动态数组里边元素的个数,相当于之前的len
}SSTable;
// 初始化链表
void ST_Init(SSTable &ST,int len){
ST.TableLen=len;
ST.elem= (ElemType*)malloc(sizeof(ElemType)*ST.TableLen);
int i;
srand(time(NULL));// 生成随机数
for(i=0;i<ST.TableLen;i++){
ST.elem[i]=rand()%100; // 为了让随机数在0-99之间
}
}
// 打印
void ST_print(SSTable ST){
for(int i=0;i<ST.TableLen;i++){
printf("%3d",ST.elem[i]);// 和获取数组方法一样
}
printf("\n");
}
// 交换位置
void swap(ElemType &a,ElemType &b){
ElemType tmp;
tmp=a;
a=b;
b=tmp;
}
// 调整子树
void AdjustDown(ElemType A[],int k,int len){
int dad=k;
int son=2*dad+1; // 左孩子下标
while (son<=len){
if(son+1<=len&&A[son]<A[son+1]){ // 看下有没有右孩子,比较左右选孩子大的
son++;
}
if(A[son]>A[dad]){ // 孩子和父亲比较,如果孩子大于父亲,那么进行交换
swap(A[son],A[dad]);
dad=son; // 孩子重新最为父亲,判断下一棵子数是否符合大根堆
son=2*dad+1;
} else{
break;
}
}
}
// 堆排序
void HeapSort(ElemType A[],int len){
int i;
// 建立大根堆
for(i=len/2;i>=0;i--){
AdjustDown(A,i,len);
}
swap(A[0],A[len]);// 交换顶部和数组最后一个元素
// 下面的策略是,不断调整剩余元素为大根堆,因为根部最大,所以再次与A[i]交换,相当于放数组后面,循环往复
for(i=len-1;i>0;i--){
AdjustDown(A,0,i);// 剩余元素调整为大根堆
swap(A[0],A[i]);
}
}
int main() {
SSTable ST;
ST_Init(ST,10);
ElemType A[10]={3,87,2,93,78,56,61,38,12,40};
memcpy(ST.elem,A, sizeof(A));
ST_print(ST);
HeapSort(ST.elem,9); // 所有元素参与排序
ST_print(ST);
return 0;
}
F:\Computer\Project\practice\17\17.5-heapSort\cmake-build-debug\17_5_heapSort.exe
3 87 2 93 78 56 61 38 12 40
2 3 12 38 40 56 61 78 87 93
进程已结束,退出代码为 0
3. 时间复杂度与空间复杂度

第三节:归并排序
1. 归并排序原理解析
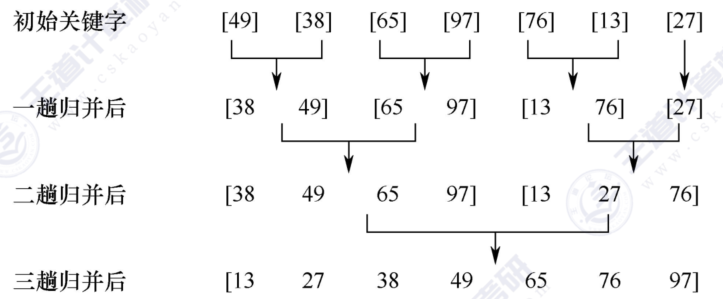
如图所示,我们把每两个元素归为一组,进行小组内排序,然后再次把两个有序小组合并为一个有序小组,不断进行,最终合并为一个有序数组。
动画演示:
https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html
2. 归并排序代码实战
归并排序的代码是采用递归思想实现的。首先,最小下标值和最大下标值相加并除以2,得到中间下标值mid,用MergeSort对low到mid排序,然后用MergeSort对mid+1到high排序。当数组的前半部分和后半部分都排好序,使用Merge函数对两个有序数组进行合并。为了提高合并有序数组效率,在Merge函数内定义了B[N]。首先,我们通过循环把数组A中从low到high的元素全部复制到B中,这是游标i从low开始,游标j从mid+1开始,谁小就将谁放入数组A,对其游标加1,并在每轮循环时对数组A的计数游标k加1。
#include <stdio.h>
#include <stdlib.h>
#define N 7
typedef int ElemType;
// 49,38,65,97,76,13,27
// 合并数组
void Merge(ElemType A[],int low,int mid,int high){
static ElemType B[N]; // 加static的目的是无论递归调用多少次,都只有一个B[N]
int i,j,k;
for(k=low;k<=high;k++){ // 赋值元素到B中
B[k]=A[k];
}
for(i=low,j=mid+1,k=i;i<=mid&& j<=high;k++){ // 合并两个有序数组
if(B[i]<=B[j]){
A[k]=B[i++];
} else{
A[k]=B[j++];
}
}
while (i<=mid){ // 如果右剩余,直接放入即可
A[k++]=B[i++]; // 前一半有剩余的放入
}
while (j<=high){
A[k++]=B[j++];//后一半的有剩余的放入
}
}
// 归并排序
void MergeSort(ElemType A[],int low,int high){
if(low<high){
int mid=(low+high)/2;
MergeSort(A,low,mid); // 排序前一半
MergeSort(A,mid+1,high); // 排序后一半
Merge(A,low,mid,high); // 将两个排序好的数组合并
}
}
// 打印
void print(int *a){
for(int i=0;i<N;i++){
printf("%3d",a[i]);
}
printf("\n");
}
int main() {
int A[7]={49,38,65,97,76,13,27}; // 数组,7个元素
print(A);
MergeSort(A,0,6);
print(A);
return 0;
}
F:\Computer\Project\practice\17\17.6-mergeSort\cmake-build-debug\17_6_mergeSort.exe
49 38 65 97 76 13 27
13 27 38 49 65 76 97
进程已结束,退出代码为 0
3. 时间复杂度与空间复杂度

第四节:小结
所有排序算法时间与空间复杂度汇总
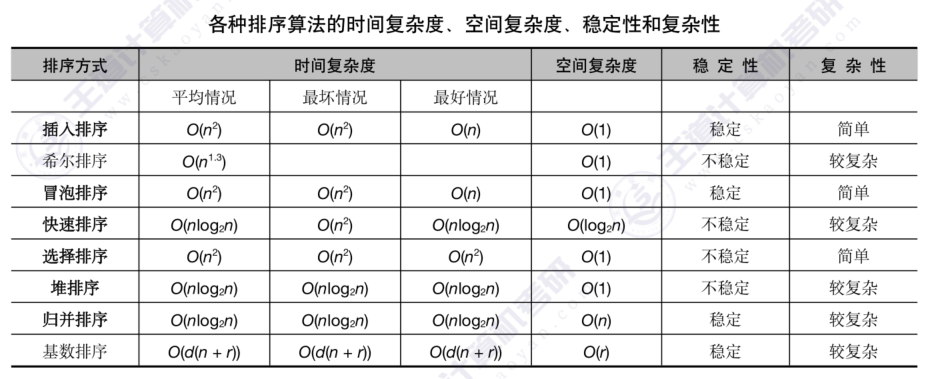
稳定性是指排序前后,相等元素位置是否会被交换。
复杂性是指代码编写的难度。

![[Flask]环境配置和项目框架的构建](https://img-blog.csdnimg.cn/e9b66250861b4178bc74dfbf6fa0a911.png)