1.概述

神经网络定义：神经网络是具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。

神经网络学习的本质：神经网络的学习本质就是不断调整各个神经元连接的权重和各个神经元的阈值。

神经网络模型最重要的两个要素：网络结构、激活函数。

神经网络运行过程：

• 获取输入内容；
• 随机初始化神经网络参数；
• 获取输出端的输出内容；
• 计算输出的误差大小；
• 根据误差调整神经网络参数；
• 对每一个样本的输入都进行上述调整并进行下一次迭代，最终即可得到收敛的模型。

2.基本单元-神经元

M-P神经元：M-P神经元是最经典的人工神经网络神经元。每个神经元都与多个输入神经元相连，这些神经元的输入信号的总和作为当前神经元的输入信号，如果该输入信号大于某个阈值，则神经元兴奋；如果小于阈值，则神经元抑制。

3.激活函数

激活函数别称：也称为响应函数或挤压函数。
激活函数的作用：使得原先只能处理线性问题的神经元模型可以用于处理非线性问题。

3.1.阶跃函数

阶跃函数的分类：阶跃函数又可以分为硬极限函数和对称阶跃函数。
硬极限函数的表达式：

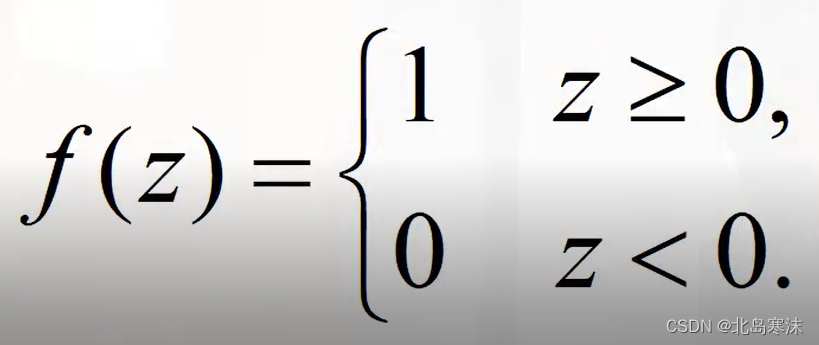
硬极限函数的特性：可以看出，硬极限函数具有开关特性：超过一定阈值兴奋，低于这个阈值抑制。
硬极限函数存在的问题：数学处理非常复杂，不能求导，不方便进行工程实现。
对称阶跃函数的表达式：

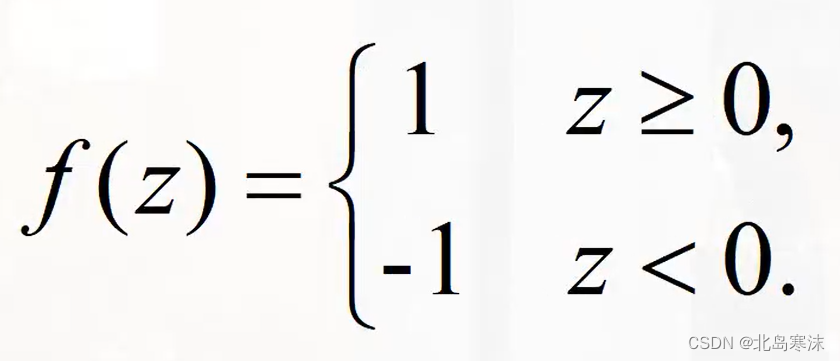
3.2.Sigmoid函数

Sigmoid函数概述：使用最广泛的激活函数。
Sigmoid函数表达式：

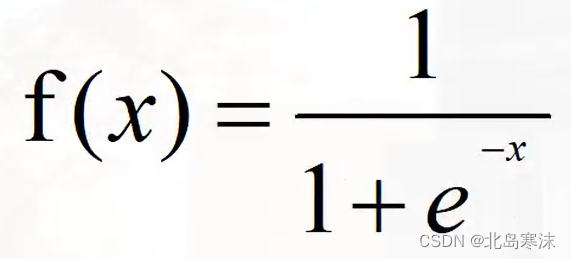
Sigmoid函数优点：具有连续容易求导，可微性和单调性的优点。
Sigmoid函数缺点：存在饱和性问题：当在正负无穷方向求导数趋近于零，而参数更新需要求导数，会使得参数无法更新，产生梯度消失现象。

3.3.TanH函数

TanH函数表达式：

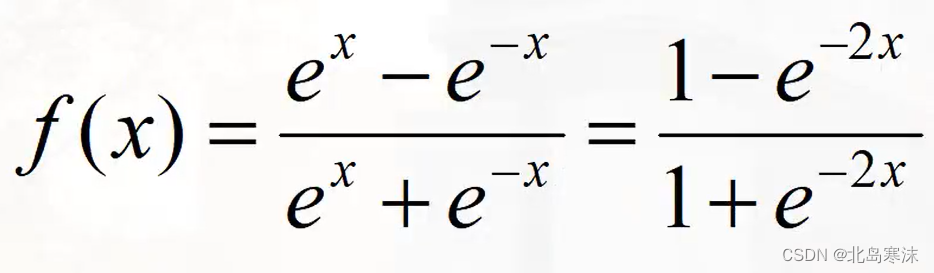
TanH函数优点：单调且可微，收敛次数比Sigmoid函数更快，可以减少迭代次数。
TanH函数缺点：仍然没有解决梯度消失的现象。

3.4.ReLU函数

ReLU函数别称：线性整流单元函数。
ReLU函数表达式：
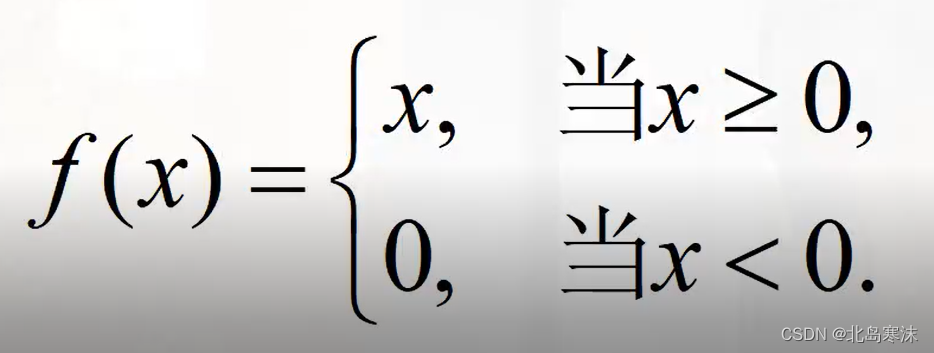ReLU函数存在的问题：在小于零区域会导致权重无法更新，影响网络的收敛性，即存在神经元坏死现象。

3.5.Softplus函数

Softplus函数性质：可以视作ReLU函数的光滑近似。
Softplus函数表达式：

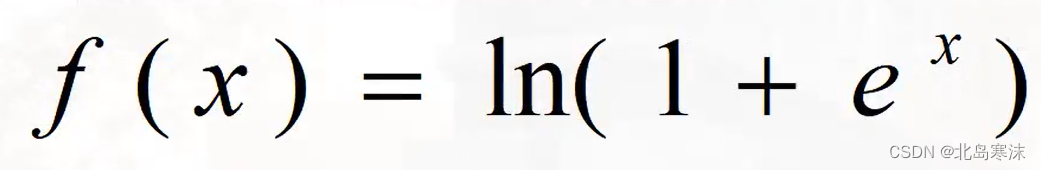
4.多层前馈神经网络

多层前馈神经网络的地位：目前最常用的神经网络结构。

多层网络的概念：多层网络是指包含隐含层的神经网络。

前馈网络的概念：网络中的神经元不存在同层连接和跨层连接。与前馈神经网络相对应的是反馈神经网络。

万有逼近性：仅需要有一个包含足够多神经元的隐层，多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数。

隐层神经元个数的确定方法：目前没有一个确定的方法，常用的方法是“试错法”。一般来说，问题越复杂，所需要的隐层神经元个数越多。

（未完待续。。。）

5.损失函数

5.1.均方误差

5.2.交叉熵

6.调参方法

6.1.梯度下降法