883. 高斯消元解线性方程组 - AcWing题库

输入一个包含 n 个方程 n 个未知数的线性方程组。

方程组中的系数为实数。

求解这个方程组。

下图为一个包含 m 个方程 n 个未知数的线性方程组示例：

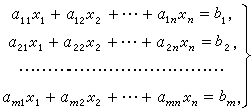
输入格式

第一行包含整数 n。

接下来 n 行，每行包含 n+1 个实数，表示一个方程的 n 个系数以及等号右侧的常数。

输出格式

如果给定线性方程组存在唯一解，则输出共 n 行，其中第 i 行输出第 i 个未知数的解，结果保留两位小数。

注意：本题有 SPJ，当输出结果为 0.00 时，输出 -0.00 也会判对。在数学中，一般没有正零或负零的概念，所以严格来说应当输出 0.00，但是考虑到本题作为一道模板题，考察点并不在于此，在此处卡住大多同学的代码没有太大意义，故增加 SPJ，对输出 -0.00 的代码也予以判对。

如果给定线性方程组存在无数解，则输出 Infinite group solutions。

如果给定线性方程组无解，则输出 No solution。

数据范围

1≤n≤100
所有输入系数以及常数均保留两位小数，绝对值均不超过 100

输入样例：

3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00

输出样例：

1.00
-2.00
3.00

 解析：高斯消元

枚举每一列c
1.找到绝对值最大的一行
2.将该行放到最上面
3.将该行第一个数变成1
4.将下面所有行的第c列的数变成0
5.最后从下往上操作使得每一行只保留一个系数

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
const int N = 100 + 5;
const double eps = 1e-6;
int n;
double a[N][N];

void out() {
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n + 1; j++) {
            cout << a[i][j] << " ";
        }
        cout << endl;
    }
    cout << endl;
}

int gauss() {
    int r, c;
    for (r = 1, c = 1; c <= n ; c++) {
        int t = r;
        //找到当前c列位置的最大值的哪一行
        for (int i = r; i <= n; i++) {  
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;
        }
        //特判，如果当前最大值是零，则跳过这一列
        if (fabs(a[t][c]) < eps)continue;
        //将当前这行放到上面
        for (int i = c; i <= n + 1; i++)swap(a[r][i], a[t][i]);
        //将这一行除以一个数使得第c列的数为1
        for (int i = n+1; i >= c; i--)a[r][i] /= a[r][c];
        //将这一行以下的每一行的第c列的数全部变为0
        for (int i = r + 1; i <= n; i++) {
            if (fabs(a[i][c]) > eps) {
                for (int j = n + 1; j >= c; j--)
                    a[i][j] -= a[r][j] * a[i][c];
            }
        }
        r++;
        //out();
    }
    //如果行数小于方程组的未知数的个数
    if (r < n-1) {
        //判断是否有0！=0的情况
        for (int i = r; i <= n; i++) {
            if (fabs(a[i][n+1]) > eps)
                return 2;//无解
        }
        return 1;//无穷多解
    }
    //操作使得每一行只有一个未知数
    for (int i = n; i >= 1; i--) {
        for (int j = i + 1; j <= n; j++)
            a[i][n+1] -= a[i][j] * a[j][n+1];
    }
    return 0;//有解
}

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n + 1; j++) {
            cin >> a[i][j];
        }
    }
    int t = gauss();
    if (t == 0) {
        for (int i = 1; i <= n; i++)
            printf("%.2lf\n", a[i][n + 1]);
    }
    else if (t == 1)cout << "Infinite group solutions" << endl;
    else cout << "No solution" << endl;
    return 0;
}